Skip to content

JA7. Graphs

Task 1

Statement

In a hostel, there are around ‘n’ number of students (assume a number above 100 for n) with rooms categorized as triple, double, and single occupancy. Explain how you will represent the above data as a graph. You need not create or share the graph but make sure to include justification for the below questions:

(i) Will the graph be a simple graph or a multi-graph?

  • A simple Graph is a graph where no vertices have self-loops and there is at most one edge between any two distinct vertices (GeeKsForGeeks, n.d.).
  • A Multi-graph is graph in which multiple edges may connect the same pair of vertices is called a multi-graph (GeeKsForGeeks, n.d.).
  • Considering our problem, I want to represent both students and rooms as vertices and edges indicating that a student is occupying a room.
  • Since a single student can occupy only one room, and students can’t occupy other students, the graph will be at most one edge between any two distinct vertices.
  • Hence, the graph will be a simple graph.

(ii) Will it have loops?

  • As the graph connect students to rooms, and a student can’t occupy themselves, and a room can’t occupy itself, the graph will not have loops.
  • Also, in the previous question, we have already established that the graph will be a simple graph, thus it can’t have loops.
  • Therefore, the graph will not have loops.

(iii) What is the possible maximum and minimum degree for each student?

  • As student can only occupy one room, the maximum degree for each student will be 1.
  • As students must occupy a room, otherwise they will be homeless, the minimum degree for each student will be 1.
  • Thus, the possible maximum and minimum degree for each student will be 1.
  • The rooms on the other hand, can have a maximum degree of 3, and a minimum degree of 0 (no students occupying the room).

(iv) If all problems are represented in the form of graphs, won’t the problems be easily visualized and solved?

  • Graphs are very powerful tools for displaying problems in a visual manner; however, they require a lot of computations to setup and solve.
  • The more the number of vertices and edges, the more the computations required to solve the problem.
  • For a very large set of vertices it becomes impractical to solve the problem using graphs.

(v)Can we represent every problem with a graph? Explain the reason by considering an example of a situation that has 11 vertices such that the degree of each vertex is 11

  • If the graph is simple, then the maximum degree of each vertex will be n-1, as each vertex can be connected to every other vertex with one edge, but not itself.
  • If we don’t have that constraint, then it is possible to have a graph with a degree of 11 for each vertex.

Task 2

A University is conducting a conference for two days on different subjects for students pursuing their higher education. Your task is to create a time slot scheduling model for the conference sessions (based on the subjects attended by students) using graph coloring. Draw the graph for the same and answer the chromatic number of this problem of scheduling time slots with the number of subjects your choice.

Let’s assume we run sessions on 3 subjects and we have 3 sessions per day per subject. For two days, we will have 18 sessions. An edge between two vertices indicates that the student is attending both the sessions.

After graphing the problem; the vertices with more edges between them can not be scheduled at the same time, as students will not be able to attend both the sessions. Thus, we need to color the graph in such a way that no two vertices with an edge between them have the same color.

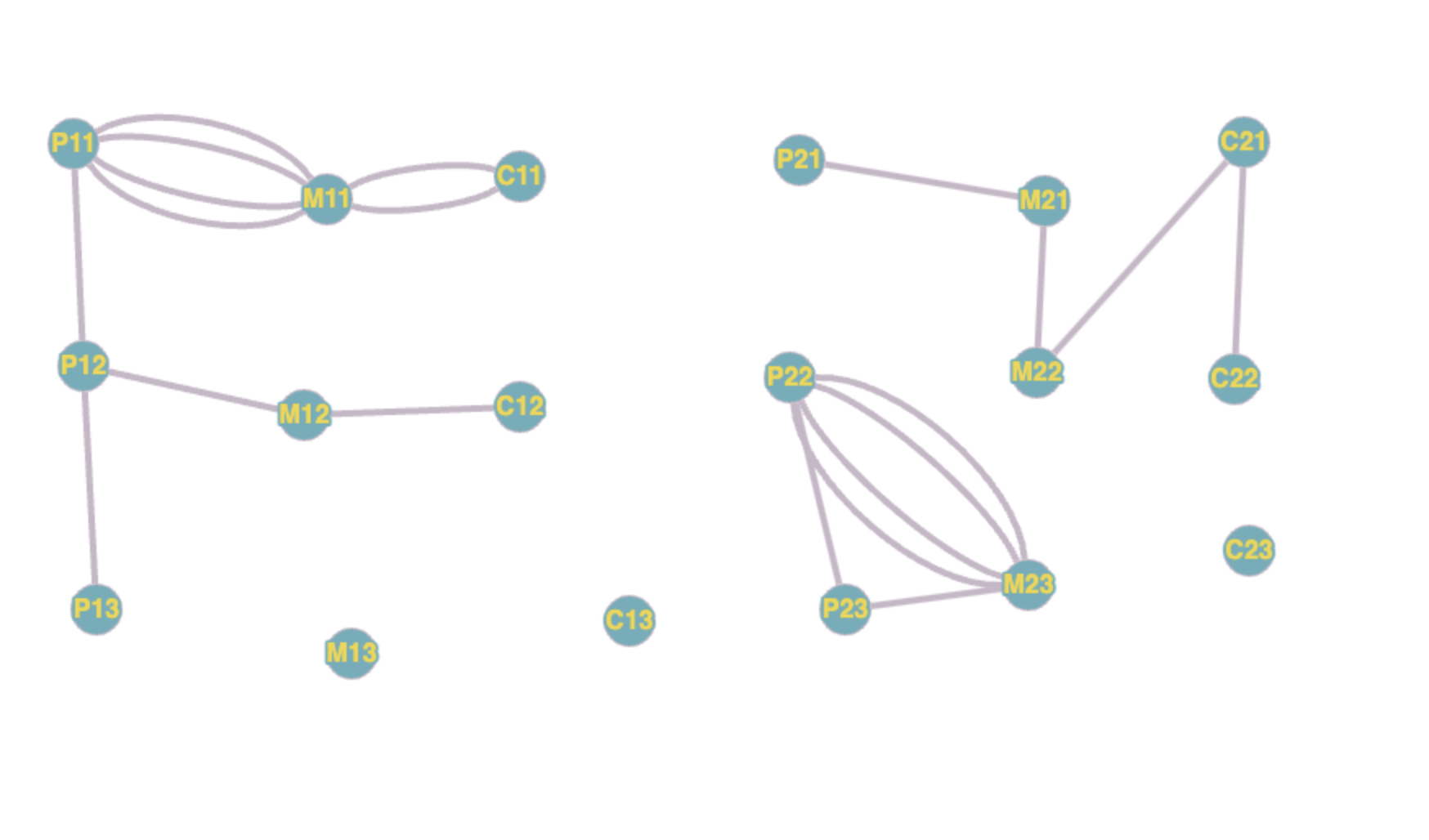
Task 3

Explain Euler and Hamiltonian cycles, and provide one simple counter example for each. Find the Euler circuit/path and Hamiltonian cycle/path for the given graph G.

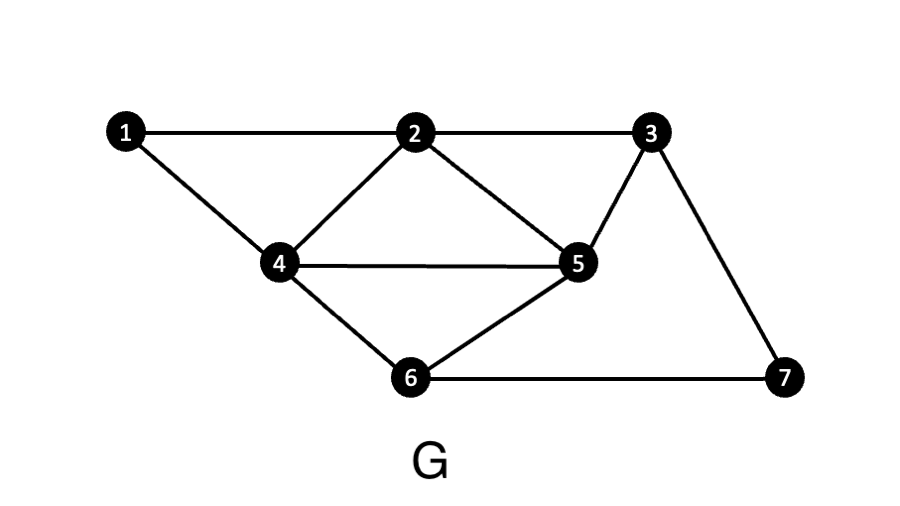
According to (GeeKsForGeeks, n.d.), Eulerian Path is a path in graph that visits every edge exactly once. Eulerian Circuit is an Eulerian Path which starts and ends on the same vertex.

Hamiltonian is similar to Eulerian, but instead of edges, it visits every vertex.

A graph that has a vertex with odd degree is a counter example for Eulerian Path, as it will not be able to visit every edge exactly once.

A graph that has a vertex with degree less than 2 is a counter example for Hamiltonian Path, as it will not be able to visit every vertex.

In the above graph, we see the vertex 3 has an odd degree (3), Thus an Eulerian circuit/path is not possible.

Hamiltonian path is possible and it is as follows: 7,6,5,3,2,4,1

Hamiltonian cycle is possible and it is as follows: 7,3,5,2,1,4,6,7

Task 4

Explain the spanning tree. Find at least two possible spanning trees for the following graph H and explain how you determined that they are spanning trees. Draw a bipartite graph from any one of the two spanning trees that you found.

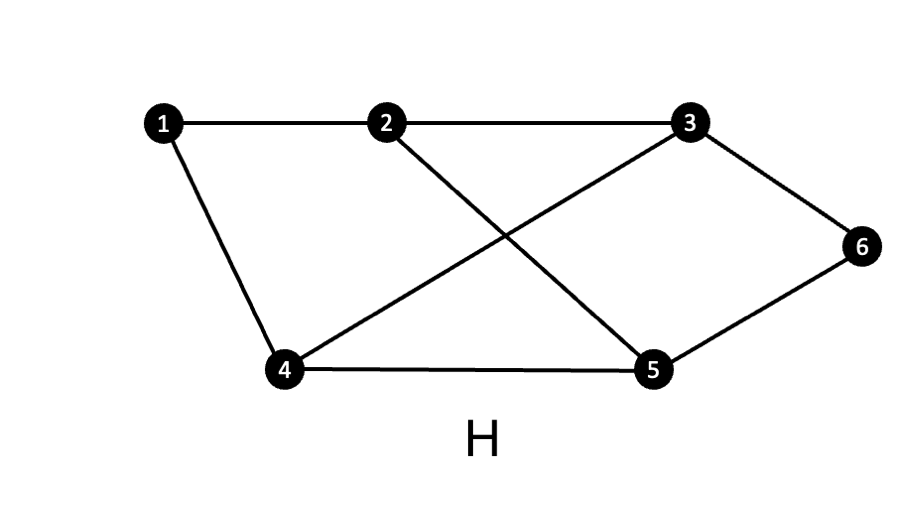
According to (TutorialsPoint, n.d.), a spanning tree is a subset of Graph G, which has all the vertices covered with minimum possible number of edges. Hence, a spanning tree does not have cycles and it cannot be disconnected.

Spanning Tree 1: 6-3, 3-1, 6-5, 5-2, 5-4 Spanning Tree 2: 3-2, 3-1, 2-5, 5-6, 5-4

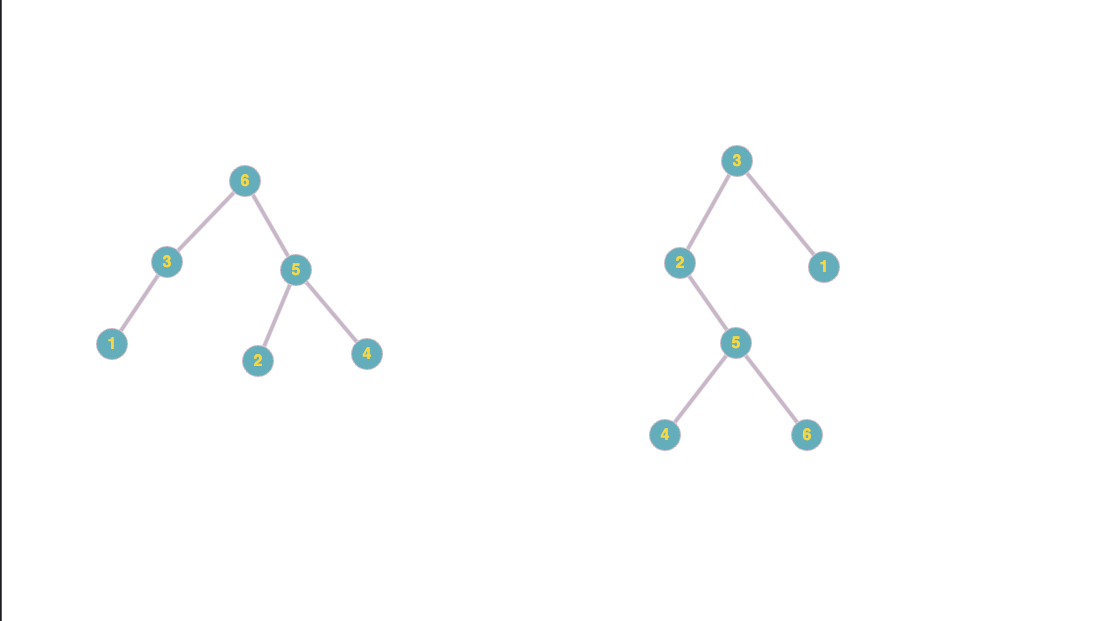
We determine that they are spanning trees because they include all elements in the graph connected with minimum number of edges.

We notice that the number of edges is equal in both trees.

References