5. Dynamic Programming¶

Unit 5 Introduction & Lectures ⁵¶

Patterns of Algorithms:
- Brute Force:
  - It is simple to implement but not but not very efficient when the input size gets large.
  - We also discussed variations of Brute force that make it a bit more efficient including the:
    - Backtracking.
    - Branch and Bound.
- Divide and Conquer:
  - It gains efficiency by breaking a large problem into subsequently smaller problems until those small problems and be easily solved and then combined together to get a solution for the larger problem.
- Greedy Algorithms:
  - It is a method for solving optimization problems.
  - It builds up a solution piece by piece, always choosing the next piece that offers the most immediate benefit.
  - Examples:
    - Dijkstra’s algorithm.
    - Prim’s algorithm.
    - Kruskal’s algorithm.
- Dynamic Programming:
  - It is an optimization technique that is applicable to problems that can be divided into overlapping subproblems.
  - Hence, it is an extension of the divide-and-conquer method.
  - The results of the repeated subproblems are stored and reused rather than recomputed.
  - The sub-problems are ordered from the easiest to solve to the hardest.
This principle of eliminating any redundant or repeated operations is the basis of dynamic programming.
The word dynamic is used because it refers to the fact that the algorithm can determine which work is redundant and then make a decision not to repeat it.
This same concept of conditional evaluation and computation appears elsewhere in computer science. In functional programming we see a similar concept referred to as Lazy evaluation.
Randomized Algorithms:
- It is an algorithm that employs a degree of randomness as part of its logic.
- The algorithm uses a randomly generated number as an input to guide its behavior, in the hope of achieving good performance in the “average case”.
- Of course this means that it is possible that an instance of running the algorithm could have poor running time, however, the goal of a randomized algorithm is to have improved performance in the average case.
In decision theory, there are two types of decision-making strategies:
- Rational decision-making:
  - This means evaluating all possible solutions and comparing advantages and disadvantages to reach the best solution.
  - This is impractical for many problems.
  - E.g., for purchasing a car, there are 10s of makers, 100s of models, and 1000s of part combinations. Choosing a car rationally is impossible.
  - We humans do not make rational decisions; otherwise, we would never make any decisions.
  - Brute force is an example of rational decision-making.
- Bounded rationality:
  - We make decisions that are as rational as possible, but there are options, factors, or considerations that we leave up to chance.
  - Randomized algorithms are a form of bounded rationality.

Pattern of Algorithms ¹¶

We discuss greed algorithms, dynamic programming, randomized algorithms, numerical algorithms, and the concept of a transform.

16.1 Greedy Algorithms¶

Examples: Kruskal’s MST, Prim’s MST, Dijkstra’s shortest paths, Huffman’s coding algorithm.
Heap is greedy; the value of any node is greater than to the values of its children.
Binary Search Tree BST is greedy; the value of any node is greater than all values in its left subtree and less than all values in its right subtree.

16.2 Dynamic Programming¶

Normal fibonacci algorithm is exponential:

int Fibr(int n) {
    if (n <= 1) return 1; // Base case
    return Fibr(n-1) + Fibr(n-2); // Recursive call
}

If you call Fibr(5), it will call Fibr(4) and Fibr(3), and Fibr(4) will call Fibr(3) and Fibr(2), and so on.
This is a redundant computation, as the results of those calls can be stored in a table and reused.
This is fibonacci with memoization:

int Fibrt(int n, int* Values) {
    // Assume Values has at least n slots, and all
    // slots are initialized to 0
    if (n <= 1) return 1; // Base case
    if (Values[n] != 0) return Values[n];
    Values[n] = Fibr(n-1, Values) + Fibr(n-2, Values);
    return Values[n];
}

The name dynamic programming comes originally from the field of dynamic control systems, which got its start before what we think of as computer programming.
The act of storing precomputed values in a table for later reuse is referred to as “programming” in that field.
Examples of problems that can be solved using dynamic programming:
- Knapsack problem.
- All-pairs shortest paths: finding the shortest path between all pairs of vertices in a graph.

16.3 Randomized Algorithms¶

Randomized algorithms are algorithms that make random choices during their execution.
This randomness indicates probability distributions over the set of possible choices.
Skip List (SL):
- It is a probabilistic data structure that is designed to overcome the basic limitation of arrays and linked lists: search and update operations are linear O(n).
- SL also solves the problem of binary search trees (AVL trees, etc) and other trees: they can be easily become unbalanced.
- SL is easier to implement than known balanced tree structures.
- SL is not guaranteed to provide good performance, but it is guaranteed to provide good performance with extremely high probability.
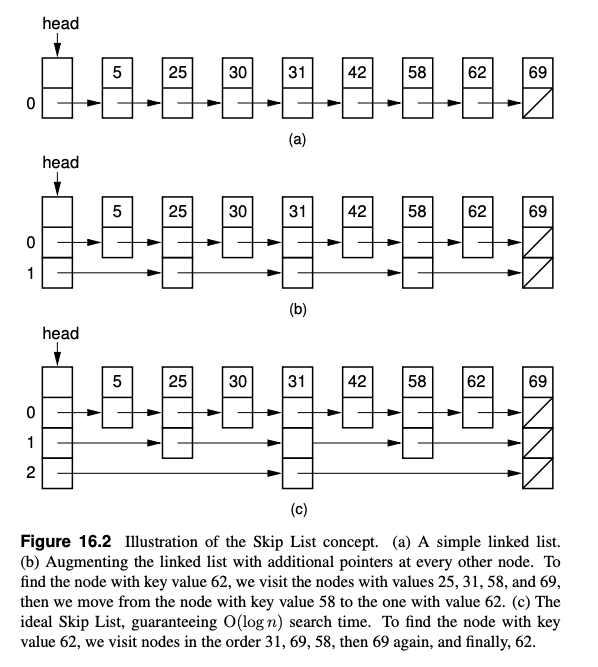
- The idea is to add multiple layers of pointers to the list, so that the search can skip over many elements at a time.
- The top layer is a list of all elements, the next layer is a list of every other element, and so on.
- When you search for an element, you start at the top layer and move down one layer at a time until you find the element or reach the bottom layer.
Example of a find function in a skip list:

bool find(const Key& K, Elem& it) const {
    SkipNode<Key,Elem> *x = head; // Dummy header node
    for (int i=level; i>=0; i--) {
        while ((x->forward[i] != NULL) && (K > x->forward[i]->k)) {
            x = x->forward[i];
        }
    }
    x = x->forward[0]; // Move to actual record, if it exists
    if ((x != NULL) && (K == x->k)) {
        it = x->it;
        return true;
    }
    else return false;
}

Maintaining the forward pointers is the key to the efficiency of the skip list, but it is expensive with the normal adding/deleting operations.
The idea is not to worry about that and choose the forward pointers randomly.

16.4 Numerical Algorithms¶

Examples of problems:
- Raise a number to a power.
- Find common factors for two numbers.
- Tell whether a number is prime.
- Generate a random integer.
- Multiply two numbers.

Dynamic Programming ²¶

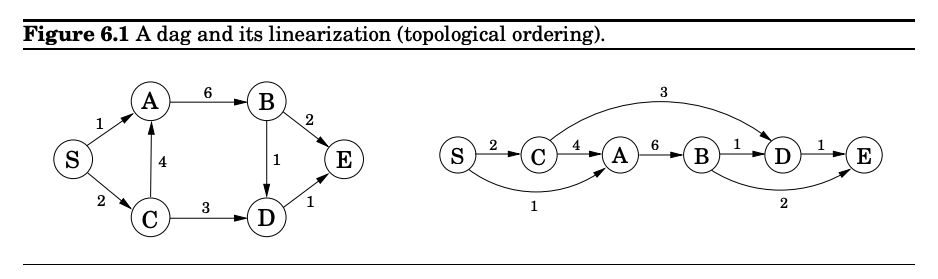
The special distinguishing feature of a dag is that its nodes can be linearized; that is, they can be arranged on a line so that all edges go from left to right.
Some problems that can be solved using dynamic programming:
- Shortest path.
- Longest common subsequence.
- Edit distance.
- Knapsack.
Every dynamic program has an underlying dag structure: think of each node as representing a subproblem, and each edge as a precedence constraint on the order in which the subproblems can be tackled.
Having nodes u1, ..., uk point to v means “subproblem v can only be solved once the answers to u1, ..., uk are known.”

Lec 15: Dynamic Programming ³¶

Lec 12: Skip Lists ⁴¶

References¶

Chapter 16: Patterns of Algorithms, Sections 16.1 - 16.2, in A Practical Introduction to Data Structures and Algorithm Analysis by Clifford A. Shaffer. ↩
Chapter 6 Dynamic Programming in Algorithms by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani available at http://www.cs.berkeley.edu/~vazirani/algorithms/chap6.pdf ↩
Dynamic Programming, By Charles E. Leiserson – MIT https://www.youtube.com/watch?v=V5hZoJ6uK-s&list=PL8B24C31197EC371C&index=15 ↩
Lec 12 | Skip Lists, By Erik Demaine – MIT (2025). Youtube.com. https://www.youtube.com/watch?v=kBwUoWpeH_Q ↩
Unit 5 Lecture 1: Dynamic Programming & Lecture 2: Randomized Algorithms. https://my.uopeople.edu/mod/book/view.php?id=453919&chapterid=554118 ↩

5. Dynamic Programming¶

Unit 5 Introduction & Lectures 5¶

Pattern of Algorithms 1¶

16.1 Greedy Algorithms¶

16.2 Dynamic Programming¶

16.3 Randomized Algorithms¶

16.4 Numerical Algorithms¶

Dynamic Programming 2¶

Lec 15: Dynamic Programming 3¶

Lec 12: Skip Lists 4¶

References¶

Unit 5 Introduction & Lectures ⁵¶

Pattern of Algorithms ¹¶

Dynamic Programming ²¶

Lec 15: Dynamic Programming ³¶

Lec 12: Skip Lists ⁴¶