Skip to content

DA8. Mini-Max Algorithm and Alpha-Beta Pruning

Statement

Explain in your own words, how the Mini-Max algorithm is used in decision-making and game theory. Make sure to explain how this algorithm applies the utility function to get the utility values for the terminal states. Feel free to add any diagram/tree structure to represent all the possible moves that allow a game to move from one state to the next state. Also, discuss how the alpha-beta pruning approach is used for optimization.

Answer

Introduction

Multi-agent systems are systems in which multiple agents interact with each other to achieve their goals. Those agents can be cooperative or competitive, and they can have different levels of knowledge about the environment and each other. Cooperative agents have common goal(s) and they share information and coordinate their actions to achieve mutual benefits. Competitive agents, on the other hand, have conflicting goals and they may try to outsmart or outmaneuver each other to maximize their individual utility, which usually happens at the expense of other agents (Poole & Mackworth, 2017).

In games, agents are usually competitive. In artificial games such as chess, tic-tac-toe or other board games, all agents have perfect knowledge about the game which can be represented as a tree using the extensive form representation. This text will start by defining mini-max algorithm giving a practical example of how it is being used; and then it will explain the alpha-beta pruning approach and how it is used for optimization and conclude with a summary of the main points.

Mini-Max Algorithm

The mini-max algorithm is a decision-making algorithm used in game theory in 2-player zero-sum games. In these games, there are two agents (players) competing against each other, and their will be only one winner, that is, one player’s win means the other’s loss. The purpose of the algorithm is to find the optimal move for a player, assuming that the opponent will also play optimally.

The algorithm works by recursively evaluating the utility of each possible move and selecting the move that maximizes the minimum utility (hence the name “minimax”) for the player (the maximizer) and minimizes the maximum utility for the opponent (the minimizer). The algorithm working can be summarized in a few steps starting from preparing the game tree according to the extensive form representation in the current moment of time and each internal node assigned a player who controls that node.

Next, evaluate the utility values of the terminal states (the leaves of the tree) using a utility function. Next, utility values are propagated upwards according to the minimax principle; that is, if the node is controlled by the maximizer, it selects the child node with the highest utility value, and if it is controlled by the minimizer, it selects the child node with the lowest utility value. This process continues until the root node is reached, at which point the optimal move for the maximizer can be determined as the branch with the highest utility value (GeeksforGeeks, 2024).

The utility function assigns a numerical value to each terminal state, representing the desirability of that state for the maximizer. The utility values can be positive, negative, or zero, depending on whether the maximizer wins, loses, or draws.

Example of Mini-Max Algorithm

To explain the mini-max algorithm, let’s consider a simple example of an XO game (tic-tac-toe), we will start from the following board state:

|     | 1   | 2  | 3  |
|  1  | ❎  | 🅾️ |    |
|  2  | ❎  | 🅾️ | ❎ |
|  3  | 🅾️  |    |    |

Let’s assume that the maximizer is the player who plays with the ❎ symbol and the minimizer is the player who plays with the 🅾️ symbol. There are 3 empty board spots that can be filled (1,3), (3,2), (3,3) and then from each branch we can follow the consequent moves by the opponent according to the following graph:

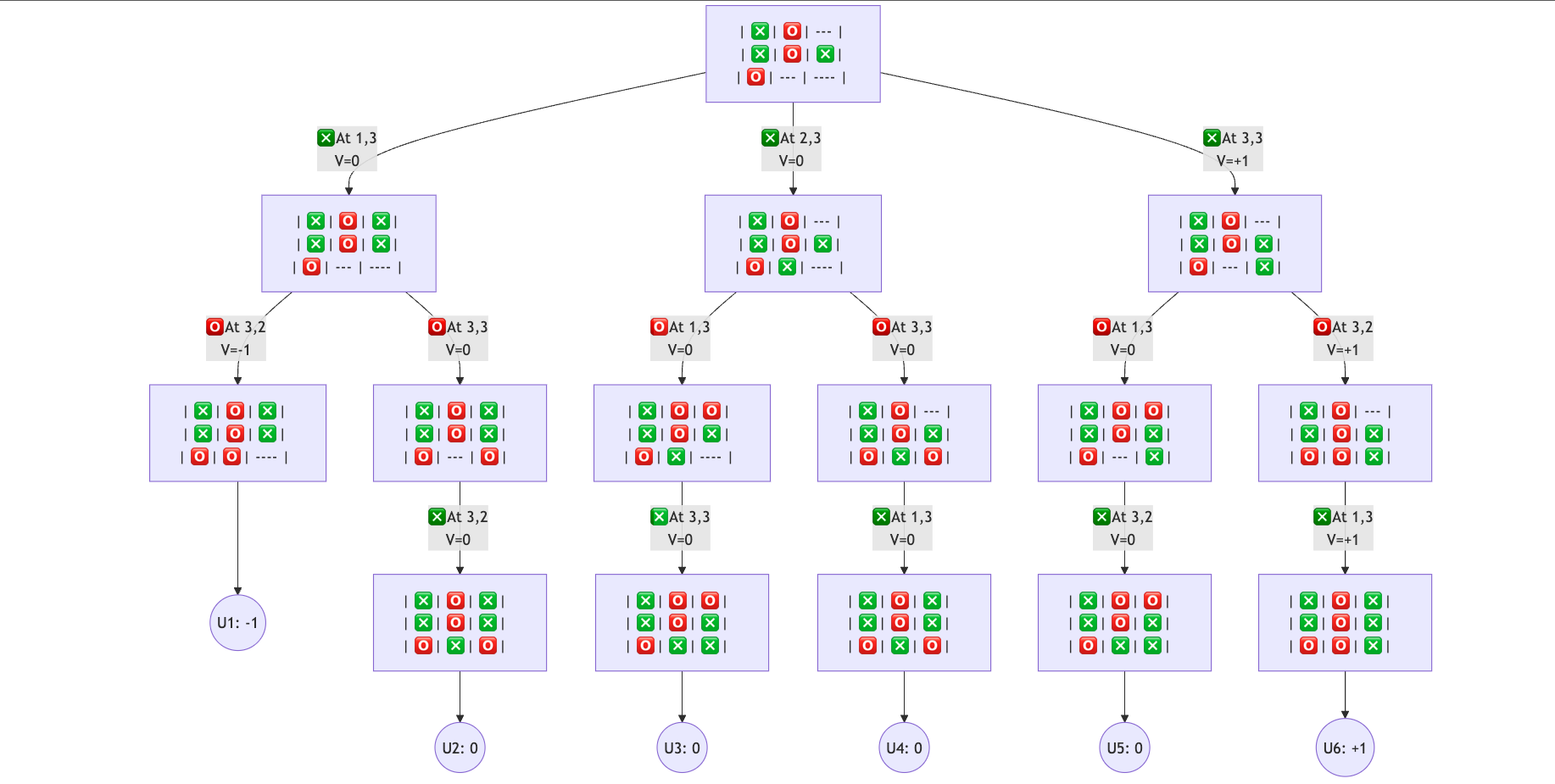
Mini-Max Algorithm

Notice that the following about the graph:

  • Edges contain a statement such as ❎ At 1,3 V=0 which means that the maximizer played ❎ at position (1,3) and the utility value of that state is 0.
  • Each level in the tree, the player alternates between the maximizer ❎ and the minimizer 🅾️.
  • The leaves of the tree are the terminal states, and the utility values are assigned to them based on the outcome of the game.
  • Possible utilities: -1, 0, +1 which represent the minimizer win, draw, and maximizer win respectively.
  • The utility values are propagated upwards according to the minimax principle. until we reach V=0 at (1,3), V=0 at (2,3), and V=+1 at (3,3).
  • The maximizer will choose the move that maximizes its utility, which is V=+1 at (3,3).
  • The player will place ❎ at (3,3) and the game will end with a win for the maximizer.

Alpha-Beta Pruning

Alpha-beta pruning is an optimization technique for the minimax algorithm that reduces the number of nodes that need to be evaluated in the game tree. The algorithm maintains two values, alpha and beta, which represent the minimum score that the maximizer is assured of and the maximum score that the minimizer is assured of, respectively. The algorithm works by pruning branches of the tree that cannot possibly change the final decision, thus reducing the number of nodes that need to be evaluated.

If the minimizer finds a move that is worse than the current alpha value, it can prune that branch of the tree, as it will not be selected by the maximizer. Similarly, if the maximizer finds a move that is better than the current beta value, it can prune that branch of the tree, as it will not be selected by the minimizer (Brennan, 2023).

References