Skip to content

JA4. More Differentiation Exercises

Question 1

1. Explain each of the following questions:

(i) When is the chain rule of the derivative used?

The chain rule states that if a function \(f\) is of the shape \(f(x) = g(h(x))\), then the derivative of \(f\) is given by \(f'(x) = g'(h(x))h'(x)\), in other words it defines how to differentiate composite functions or functions of functions (Khan Academy, n.d).

(ii) What is the underlying algebraic principle behind the chain rule used to find the derivative. Give an example.(Ensure that you provide self-made examples and explanations, do not copy from the available resources)?

The underlying algebraic principle behind the chain rule is that if you do opposite the differentiation process (integration), we must get the original function back, and that’s what the chain rule ensures.

Let’s assume

\[ \begin{aligned} h(x) &= x^2 + 1 \\ g(x) &= ln(x) \\ g'(x) &= \frac{1}{x} \\ h'(x) &= 2x \\ f(x) &= ln(x^2 + 1) \\ \end{aligned} \]

Then, we can differentiate \(f(x) = g(h(x))\) as follows

\[ \begin{aligned} f(x) &= g(h(x)) \\ &= ln(x^2 + 1) \\ f'(x) &= g'(h(x))h'(x) \\ &= \frac{1}{x^2 + 1} \cdot 2x \\ &= \frac{2x}{x^2 + 1} \end{aligned} \]

Question 2

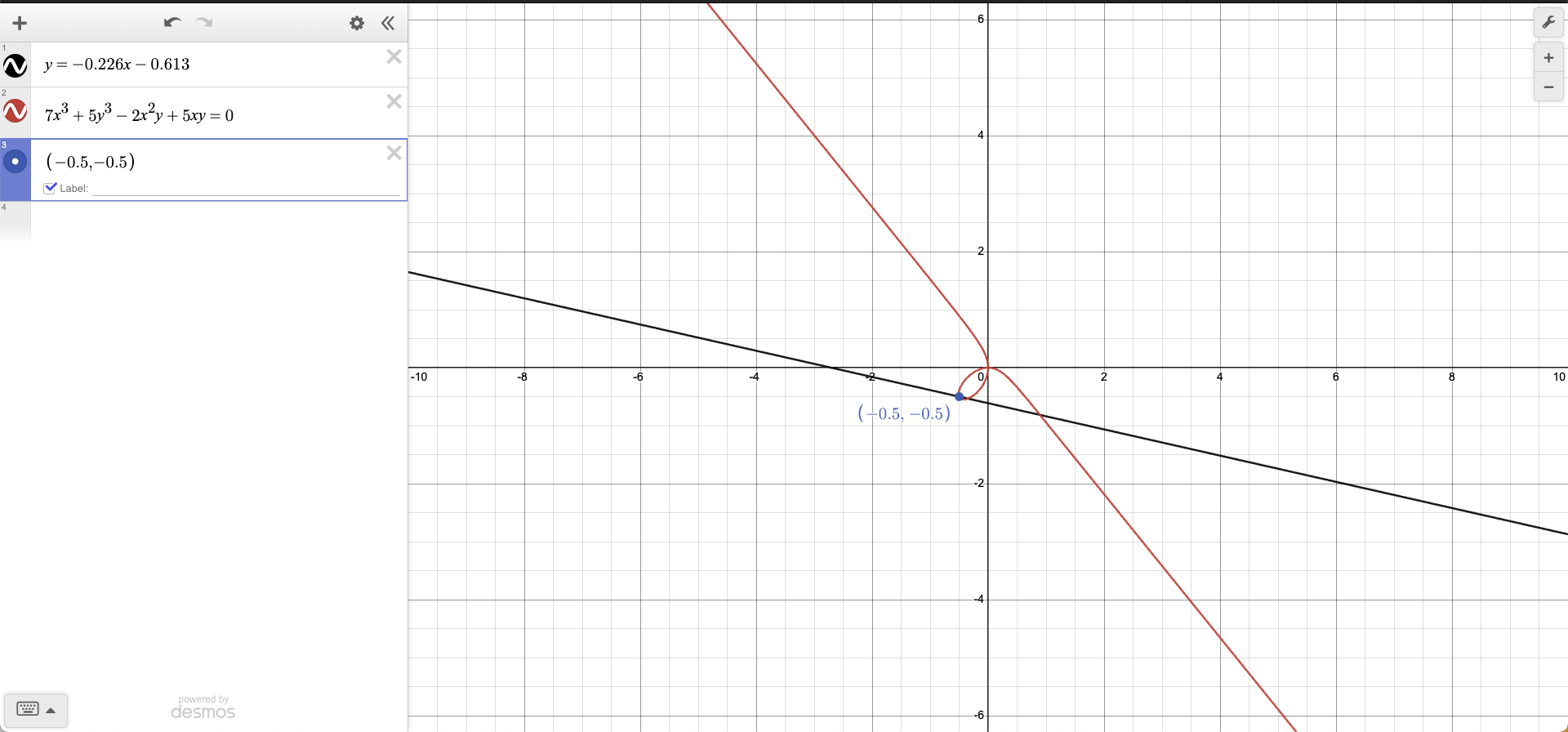
2. Find an approximated equation of a tangent line to the folium curve \(7x^3 +5y^3 - 2x^2y+ 5xy = 0\) at the point (-0.5, -0.5) using implicit differentiation. Please show the step-by-step working of the problem.

Let’s find \(\frac{dy}{dx}\) of the implicit function \(7x^3 +5y^3 - 2x^2y+ 5xy = 0\).

\[ \begin{aligned} 7x^3 +5y^3 - 2x^2y+ 5xy &= 0 \\ \frac{d}{dx}(7x^3 +5y^3 - 2x^2y+ 5xy) &= \frac{d}{dx}(0) \\ \frac{d}{dx}(7x^3) + \frac{d}{dx}(5y^3) - \frac{d}{dx}(2x^2y) + \frac{d}{dx}(5xy) &= 0 \\ 3 \cdot 7x^2 + 3 \cdot 5y^2 \cdot \frac{dy}{dx} - (2 \cdot 2x \cdot y + 2x^2 \cdot \frac{dy}{dx}) + (5y + 5x \cdot \frac{dy}{dx}) &= 0 \\ 21x^2 + 15y^2 \cdot \frac{dy}{dx} - 4xy - 4x^2 \cdot \frac{dy}{dx} + 5y + 5x \cdot \frac{dy}{dx} &= 0 \\ (15y^2 - 4x^2 + 5) \cdot \frac{dy}{dx} + (21x^2- 4xy + 5y) &= 0 \\ (15y^2 - 4x^2 + 5) \cdot \frac{dy}{dx} = -(21x^2- 4xy + 5y) \\ \frac{dy}{dx} = -\frac{21x^2- 4xy + 5y}{15y^2 - 4x^2 + 5} \\ \end{aligned} \]

The slope of the tangent line at the point (-0.5, -0.5) equals the value of \(\frac{dy}{dx}\) at that point, so let’s plug in x = -0.5 and y = -0.5 into the \(\frac{dy}{dx}\) equation above.

\[ \begin{aligned} \frac{dy}{dx} &= -\frac{21x^2- 4xy + 5y}{15y^2 - 4x^2 + 5} \\ &= -\frac{21(-0.5)^2- 4(-0.5)(-0.5) + 5(-0.5)}{15(-0.5)^2 - 4(-0.5)^2 + 5} \\ &= -\frac{21 \cdot 0.25 - 4 \cdot 0.25 - 5 \cdot 0.5}{15 \cdot 0.25 - 4 \cdot 0.25 + 5} \\ &= −0.225806451613 \\ &\approx -0.226 \end{aligned} \]

Now let’s use the point (-0.5, -0.5) and the slope -0.226 to find the equation of the tangent line.

\[ \begin{aligned} y - y_1 &= m(x - x_1) \\ y - (-0.5) &= -0.226(x - (-0.5)) \\ y + 0.5 &= -0.226(x + 0.5) \\ y + 0.5 &= -0.226x - 0.113 \\ y &= -0.226x - 0.613 \end{aligned} \]

Now, I’ll use Desmos to plot the folium curve and the tangent line.

References