WA4. Binary Tree Search Algorithm Assignment¶
Contents¶
Statement¶
For the unit 4 assignment:
- You are to construct and perform traversal on a binary search tree.
- Your algorithm must be written in the Java language and developed using the Jeliot algorithm animation environment.
- Your binary tree will contain a series of integers. Your algorithm must be able to accommodate a variable number of integers and all of these items must be entered by the user of the program by prompting for each integer from standard input.
- You must submit both a description of the assignment and how your algorithm works including an Asymptotic analysis of your algorithm.The scope of your asymptotic analysis should only include the binary search portion of your assignment.
- You must include the code of your algorithm.
- You must include a screen shot or other capture of the output of you binary search tree that indicates the number of iterations that were required to find the search value.
Requirements¶
- Your algorithm must take each integer entered by the user and insert it into a binary search tree. You can use either an**array or linked list implementation to create your binary tree structure**.
- When all of the values have been populated into the tree (you must figure out how to determine when the last value has been entered into your program), your algorithm must:
- prompt the user for a search value.
- perform a search of your binary tree and report the number of iterations that were required to find the value.
Conclusion¶
- Running the attached code will interactively ask the user to select a
Commandthen perform the corresponding action. - Supported commands are:
insert: insert a new value into the tree.search: search for a value in the tree.traverse: traverse the tree, and then print the output in a human-readable format.exit: exit the program.
- Below is a screenshot showing the output of the following sequence of commands:
insert 1insert 5insert 2traverse: prints 1, 2, 5.search 2: printsValue 2 found, iterations consumed: 3search 6printsValue 6 not foundexit
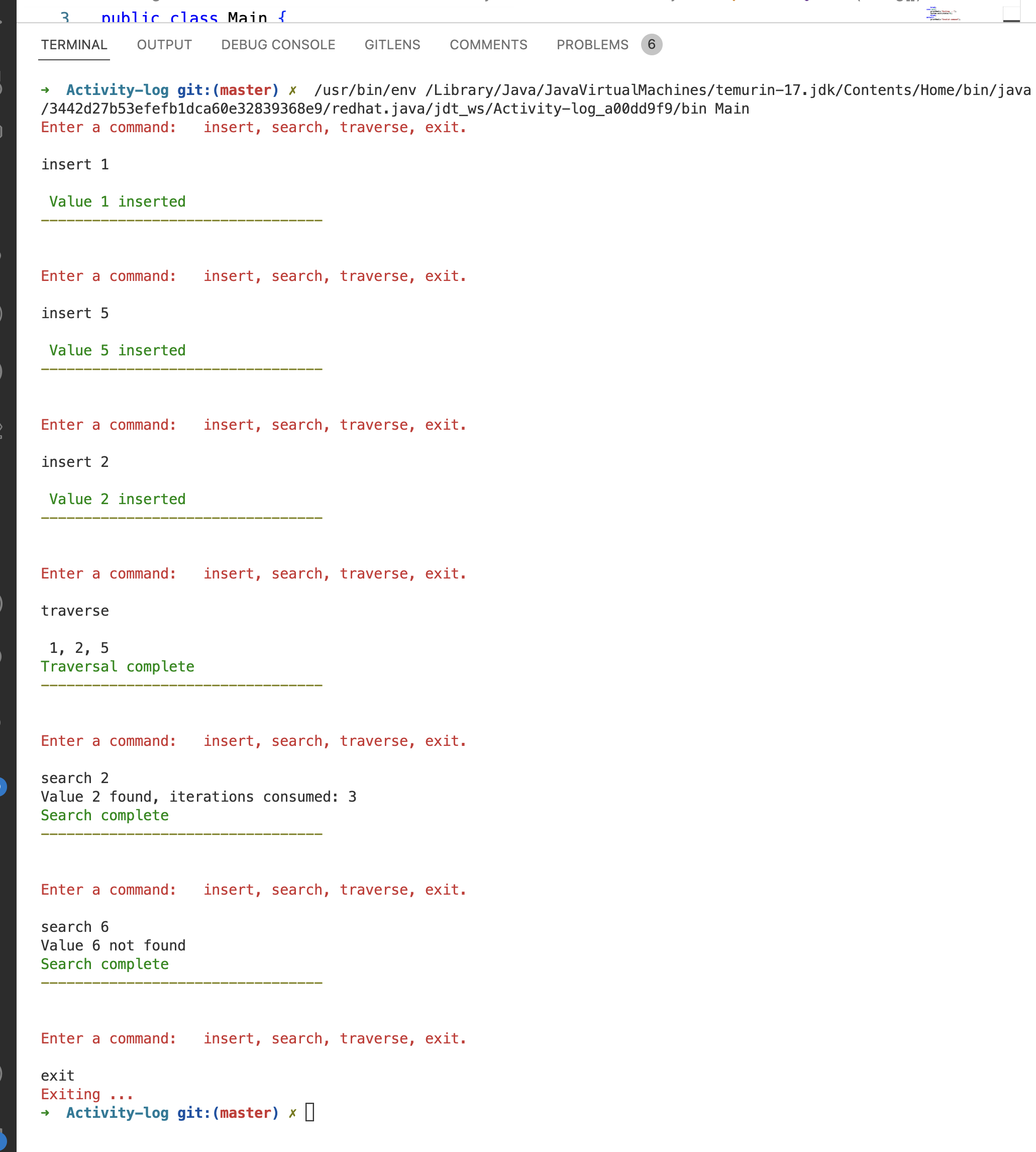
- We notice that according to the sequence of values that we inserted, the tree is not balance, and the search operation consumed 3 iterations to find the value 2.
- The text chose
LinkedListto implement the tree, because it is easier to implement and visualize, however,no self-balancing functionality is implemented. - The text will include the runtime analysis of the program and then explains the code.
Important Notes¶

- The code is written for Java SE Development Kit 17.0.2 as shown in the screenshot above.
- Unfortunately, the JeLiot plugin is not compatible with Java 17, so the code is not visualized using JeLiot.
- Please run this code using Java 17 or higher; although it might work with older versions, but it is not tested and not guaranteed to work.
Runtime Analysis¶
- The text will discuss the runtime analysis for the
MBinarySearchTreeclass that is included in./MBinarySearchTree.javafile. - The table below shows the runtime analysis for each method in the class,
| Method | Runtime Complexity (lower bound) | Runtime Complexity (worst case) | Comment |
|---|---|---|---|
| isEmpty, size, getRoot, setRoot | O(1) | O(1) | Simple constant operations |
| insert | O(log n) | O(n) | If the tree is not balanced, it becomes just a linear linked list (Barnett & Del Tongo, 2008). |
| contains | O(log n) | O(n) | If the tree is not balanced, we keep going on one direction until we traverse all nodes (Barnett & Del Tongo, 2008). |
| getDepth | O(log n) | O(n) | |
| search | 2 * O(log n) = O (log n) | 2 * O(n) = O(n) | This function wraps both contains and getDepth (to count iterations) functions. |
| traverse | O(n) | O(n) | All nodes must be visited. |
Code Walkthrough¶
Main Class¶
- This is the entry point of the program.
- It starts by instantiating a new empty
MBinarySearchTreeobject. - Then it enters an infinite loop that will keep asking the user for a command and then perform the corresponding action.
- The code defines a
Commandenum that contains all supported commands. - When the user enters a command, the code will parse it and then perform the corresponding action.
- The code will keep asking the user for a command until the user enters the
exitcommand. - There are 4 functions that are used to print colored text to the console, they are used to make the output more readable.
import java.util.Scanner;
public class Main {
public static void printYellow(String s) {
System.out.println("\033[0;33m" + s + "\n\033[0m");
}
public static void printGreen(String s) {
System.out.println("\033[0;32m" + s + "\033[0m");
}
public static void printRed(String s) {
System.out.println("\033[0;31m" + s + "\033[0m");
}
enum Command {
insert, search, traverse, exit
}
public static void promptForCommand(MBinarySearchTree tree) {
String allCommandsString = "";
Command[] allCommands = Command.values();
for (int i = 0; i < allCommands.length; i++) {
boolean isLastCommand = i == allCommands.length - 1;
String command = allCommands[i].toString();
String delimiter = isLastCommand ? "." : ", ";
allCommandsString += command + delimiter;
}
printRed("Enter a command: " + allCommandsString + "\n");
Scanner scanner = new Scanner(System.in);
String input = scanner.nextLine().trim();
String[] inputArray = input.split(" ");
String commandString = inputArray[0];
Integer valueEmbeddedWithCommand = null;
if (inputArray.length > 1) {
try {
valueEmbeddedWithCommand = Integer.parseInt(inputArray[1]);
} catch (ArrayIndexOutOfBoundsException e) {
printRed("Invalid command");
printRed("Enter one the following commands: " + allCommandsString + "\n");
printYellow("--------------------------------- \n");
promptForCommand(tree);
scanner.close();
return;
}
}
Command command;
try {
command = Command.valueOf(commandString);
} catch (IllegalArgumentException e) {
printRed("Invalid command");
printRed("Enter one the following commands: " + allCommandsString + "\n");
printYellow("--------------------------------- \n");
promptForCommand(tree);
scanner.close();
return;
}
switch (command) {
case insert:
if (valueEmbeddedWithCommand == null)
System.out.println("Enter a value to insert: ");
int value = valueEmbeddedWithCommand != null ? valueEmbeddedWithCommand
: scanner.nextInt();
tree.insert(value);
printGreen("\n Value " + value + " inserted");
printYellow("--------------------------------- \n");
promptForCommand(tree);
break;
case search:
if (valueEmbeddedWithCommand == null)
System.out.println("Enter a value to search: ");
int v = valueEmbeddedWithCommand != null ? valueEmbeddedWithCommand : scanner.nextInt();
tree.search(v);
printGreen("Search complete");
printYellow("--------------------------------- \n");
promptForCommand(tree);
break;
case traverse:
tree.traverse();
printGreen("Traversal complete");
printYellow("--------------------------------- \n");
promptForCommand(tree);
break;
case exit:
printRed("Exiting ...");
System.exit(0);
break;
default:
printRed("Invalid command");
printRed("Enter one the following commands: " + allCommandsString + "\n");
printYellow("--------------------------------- \n");
promptForCommand(tree);
break;
}
scanner.close();
}
public static void main(String[] args) {
MBinarySearchTree tree = new MBinarySearchTree();
promptForCommand(tree);
}
}
MBinarySearchTree Class¶
- This class is the implementation of the binary search tree that has been discussed in the text.
- The class supports the following functions:
isEmpty: returns true if the tree is empty, false otherwise.size: returns the number of nodes in the tree.getRoot: returns the root node of the tree.setRoot: sets the root node of the tree.insert: inserts a new value into the tree, it finds the correct position for the new value and inserts it there.contains: searched for a value within the tree and return the MNode that holds this value.getDepth: returns the depth of a node within the tree.search: wraps thecontainsandgetDepthfunctions to search for a value within the tree and return the depth of the node that holds this value (aka, number of iterations).traverse: traverses the tree in-order and prints the values of all nodes, it uses a Queue to keep track of the nodes that need to be visited and then dequeue them and print their values in the correct order.
public class MBinarySearchTree {
MNode root;
int size;
public MBinarySearchTree(int root) {
this.root = new MNode(root);
}
public MBinarySearchTree(int root, MNode left, MNode right) {
this.root = new MNode(root, left, right);
}
public MBinarySearchTree() {
this.root = null;
}
public boolean isEmpty() {
return this.root == null && this.size == 0;
}
public int size() {
return this.size;
}
public MNode getRoot() {
return this.root;
}
public void setRoot(MNode root) {
if (!this.isEmpty()) {
throw new IllegalStateException("Cannot set root of non-empty tree");
}
this.root = root;
}
/*
* Allowing for duplicates, duplicates will be inserted to the right of the
* current node
*/
private void insert(int value, MNode root) {
MNode newNode = new MNode(value);
if (root == null) {
this.root = newNode;
this.size++;
return;
}
MNode currentMNode = root;
MNode newNodeParent = null; // we can't not tell where to place new node yet.
boolean insertRight = false;
while (currentMNode != null) {
newNodeParent = currentMNode;
if (value >= currentMNode.getValue()) {
currentMNode = currentMNode.getRight();
insertRight = true;
} else {
currentMNode = currentMNode.getLeft();
insertRight = false;
}
}
if (insertRight) {
newNodeParent.setRight(newNode);
} else {
newNodeParent.setLeft(newNode);
}
this.size++;
}
public void insert(int value) {
this.insert(value, this.root);
}
public void insert(int[] values) {
for (int value : values) {
this.insert(value);
}
}
private MNode contains(int value, MNode root) {
if (root == null) {
return null;
}
MNode currentMNode = root;
MNode leftNode = currentMNode.getLeft();
MNode rightNode = currentMNode.getRight();
int currentMNodeValue = currentMNode.getValue();
boolean searchRight = value >= currentMNodeValue;
if (currentMNodeValue == value) {
return currentMNode;
} else if (searchRight && rightNode == null) {
return null;
} else if (!searchRight && leftNode == null) {
return null;
} else if (searchRight) {
return contains(value, rightNode);
} else {
return contains(value, leftNode);
}
}
public void search(int value) {
MNode found = this.contains(value, this.root);
if (found == null) {
System.out.println("Value " + value + " not found");
} else {
int iterations = this.getDepth(this.root, found) + 1;
System.out.println("Value " + value + " found, iterations consumed: " + iterations);
}
}
private void inOrder(MNode root, MQueue<Integer> values) {
if (root == null) {
return;
}
MNode currentMNode = root;
MNode leftNode = currentMNode.getLeft();
MNode rightNode = currentMNode.getRight();
inOrder(leftNode, values);
values.enqueue(currentMNode.getValue());
inOrder(rightNode, values);
}
public void traverse() {
MQueue<Integer> values = new MQueue<Integer>(this.size());
this.inOrder(this.root, values);
String output = "";
while (!values.isEmpty()) {
output += values.dequeue() + ", ";
}
System.out.println("\n " + output.substring(0, output.length() - 2));
}
private int getDepth(MNode root, MNode node) {
if (root == null) {
return -1;
}
MNode currentMNode = root;
int currentMNodeValue = currentMNode.getValue();
if (currentMNodeValue == node.getValue()) {
return 0;
}
MNode leftNode = currentMNode.getLeft();
MNode rightNode = currentMNode.getRight();
boolean goRight = node.getValue() > currentMNodeValue;
if (goRight) {
return 1 + getDepth(rightNode, node);
} else {
return 1 + getDepth(leftNode, node);
}
}
}
MNode Class¶
- This class represents a node within the binary search tree.
- It encapsulates the functionality of maintaining pointers to the left and right nodes along with the value of the node.
public class MNode {
public int value;
public MNode left;
public MNode right;
public MNode(int value) {
this.value = value;
this.left = null;
this.right = null;
}
public MNode(int value, MNode left, MNode right) {
this.value = value;
this.left = left;
this.right = right;
}
public int getValue() {
return value;
}
public void setValue(int val) {
this.value = val;
}
public MNode getLeft() {
return left;
}
public void setLeft(MNode left) {
this.left = left;
}
public MNode getRight() {
return right;
}
public void setRight(MNode right) {
this.right = right;
}
public boolean isLeaf() {
return this.left == null && this.right == null;
}
}
MQueue Class¶
- This class represents a queue data structure that was discussed in the previous week.
public class MQueue<T> {
private T[] queue;
private int front;
private int rear;
private int size;
@SuppressWarnings("unchecked")
public MQueue(int size) {
this.size = size;
queue = (T[]) new Object[size];
front = -1;
rear = -1;
}
public void enqueue(T item) {
if (rear == size - 1) {
System.out.println("MQueue is full");
} else {
if (front == -1) {
front = 0;
}
rear++;
queue[rear] = item;
}
}
public T dequeue() {
if (front == -1) {
System.out.println("MQueue is empty");
return null;
} else {
T item = queue[front];
if (front == rear) {
front = -1;
rear = -1;
} else {
front++;
}
return item;
}
}
public boolean isEmpty() {
return front == -1;
}
public boolean isFull() {
return rear == size - 1;
}
public int length() {
return rear - front + 1;
}
}
References¶
- Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf. Chapter 5.
- Barnett, G. & Del Tongo, L. (2008). Data Structures and Algorithms: An Annotated Reference with Examples. Chapter 3: Binary Search Tree and Chapter 4: Heaps.