Skip to content

WA5. Knapsack Problem - Dynamic Programming

Statement

A thief robbing a store can carry a maximum weight of W in their knapsack. There are n items and ith item weighs wi and is worth vi dollars. What items should the thief take to maximize the value of what is stolen?

The thief must adhere to the 0-1 binary rule which states that only whole items can be taken. The thief is not allowed to take a fraction of an item (such as ½ of a necklace or ¼ of a diamond ring). The thief must decide to either take or leave each item.

Input:

  • Maximum weight (W) that can be carried by the thief is 20 pounds.
  • There are 16 items in the store that the thief can take (n = 16).
  • Their values and corresponding weights are defined by the following two lists:
    • Item Values: 10, 5, 30, 8, 12, 30, 50, 10, 2, 10, 40, 80, 100, 25, 10, 5.
    • Item Weights: 1, 4, 6, 2, 5, 10, 8, 3, 9, 1, 4, 2, 5, 8, 9, 1.

Instructions:

  • Develop an algorithm using Java and developed in the Cloud9 environment (or your own Java IDE) environment to solve the knapsack problem.
  • Your solution should be based upon dynamic programming principles as opposed to brute force.
  • The optimal solution is one that is less than or equal to 20 pounds of weight and one that has the highest value.

Brute Force Algorithm:

  • The brute force approach would be to look at every possible combination of items that is less than or equal to 20 pounds.  We know that the brute force approach will need to consider every possible combination of items which is 2n items or 65536.

Table of Contents

Introduction

The knapsack problem involves finding the optimal combination of items to include in a knapsack, given a set of items with different weights and values, and a knapsack with a maximum weight capacity. The goal is to maximize the total value of carried items without exceeding the weight capacity of the knapsack (Shaffer, 2011).

The dynamic programming approach to the knapsack problem involves breaking down the problem into smaller subproblems and solving them only once; and then memoize the results to solve larger problems. The key idea is to build a table to store the maximum value that can be achieved with a given weight capacity and a subset of items. The table is filled iteratively, starting with the smallest subproblem and building up to the full problem (Hristakeva & Shrestha, 2005).

This assignment provides a source code in java, an explanation of the source code, and example output. To run the code, you need to compile the source code and then run it. All files should be passed with the attachments.

To run the code, you need to:

  1. Compile the java code using the command javac Wa5.java.
  2. Run the compiled code using the command java Wa5.

Source Code

Below is the source code for the assignment, all in one file, to make easy to run and test. The main class is Wa5 which contains other helper classes and methods to implement the dynamic programming solution to the knapsack problem.

import java.util.ArrayList;
import java.util.List;

class Wa5 {

    public static void main(String[] args) {
        int[] weights = { 1, 4, 6, 2, 5, 10, 8, 3, 9, 1, 4, 2, 5, 8, 9, 1 }; // weights of items available to steal
        int[] Values = { 10, 5, 30, 8, 12, 30, 50, 10, 2, 10, 40, 80, 100, 25, 10, 5 }; // values of items available to steal
        int maxWeight = 20; // maximum weight that can be carried by the thief
        int n = weights.length; // number of items available to steal

        ShopItem[] shopItems = new ShopItem[n];
        for (int i = 0; i < n; i++) {
            shopItems[i] = new ShopItem(weights[i], Values[i]);
        }

        KnapSack k = new KnapSack(shopItems, maxWeight);
        k.solve();
    }

    public static class KnapSack {

        private ShopItem[] items; // items available to steal
        private int maxWeight; // maximum weight that can be carried by the thief
        private int[][] dp; // dynamic programming table

        public KnapSack(ShopItem[] items, int maxWeight) {
            this.items = items;
            this.maxWeight = maxWeight;
            this.dp = new int[items.length + 1][maxWeight + 1]; // initialize the dp table [n * W]
        }

        public void populateTable() {
            for (int i = 1; i <= items.length; i++) { // loop through the items
                for (int j = 1; j <= maxWeight; j++) { // loop through capacities
                    if (items[i - 1].weight <= j) { // if the weight of the item is less than or equal to the current capacity (j)
                        int aboveCell = dp[i - 1][j]; // value of the cell above the current cell
                        int remainingWeight = j - items[i - 1].weight; // remaining weight after including the item in the knapsack
                        int valueOfItem = items[i - 1].value; // value of the item
                        int valueOfItemPlusRemaining = dp[i - 1][remainingWeight] + valueOfItem; // value of the item plus the remaining weight
                        int cellValue = Math.max(aboveCell, valueOfItemPlusRemaining); // put the maximum value in the cell
                        dp[i][j] = cellValue; // set the value of the cell
                    } else {
                        // we can not include the item in the knapsack, so we just copy the value from the cell above
                        dp[i][j] = dp[i - 1][j];
                    }
                }
            }
        }

        public void reportResults() {
            // let's print the dp table
            System.out.println("DP Table:");
            System.out.printf("%10s", "i/j"); // blank space for row header

            // headers for the columns
            for (int j = 0; j <= maxWeight; j++) {
                System.out.printf("%8d", j);
            }
            System.out.println();

            // rows
            for (int i = 0; i <= items.length; i++) {
                if (i == 0) {
                    System.out.printf("%10s", "0");
                } else {
                    System.out.printf("%10s", " " + i);
                }
                for (int j = 0; j <= maxWeight; j++) {
                    System.out.printf("%8d", dp[i][j]);
                }
                System.out.println();
            }

            // We will try to report the items that were taken, and their total value.
            // there are simpler and less expensive ways to do this, e.g. totalValue = dp[n][maxWeight]
            // but we will use the most straightforward way
            List<ShopItem> itemsTaken = new ArrayList<>();
            int totalValue = 0;
            int w = maxWeight;
            for (int i = items.length; i > 0 && w > 0; i--) {
                if (dp[i][w] != dp[i - 1][w]) { // if the value of the cell is not equal to the value of the cell above
                    itemsTaken.add(items[i - 1]);
                    totalValue += items[i - 1].value; // Adjust the totalValue.
                    w -= items[i - 1].weight; // track the remaining weight
                }
            }

            System.out.println("\n\n\n");
            System.out.println("Total value taken by thief: " + totalValue);
            System.out.println("Items taken:");
            for (ShopItem item : itemsTaken) {
                System.out.println("\t - Weight: " + item.weight + ", Value: " + item.value);
            }
        }

        public void solve() {
            populateTable();
            reportResults();
        }
    }

    public static class ShopItem {

        int weight;
        int value;

        public ShopItem(int weight, int value) {
            this.weight = weight;
            this.value = value;
        }
    }
}

Source Code Explanation

  • The main class Wa5 contains a main method that orchestrates the solution to the knapsack problem along with two helper classes: KnapSack and ShopItem.
  • The ShopItem class represents an item available in the store with two attributes: weight and value.
  • The KnapSack class represents the knapsack problem and contains the logic to solve it using dynamic programming principles.
  • The KnapSack class has the following attributes and methods:
    • items: an array of ShopItem objects representing the items available in the store.
    • maxWeight: an integer representing the maximum weight that can be carried by the thief.
    • dp: a two-dimensional array to store the results of subproblems.
    • populateTable(): a method to fill the dynamic programming table with the maximum value that can be achieved with a given weight capacity and a subset of items according to method from (Hristakeva & Shrestha, 2005).
    • reportResults(): a method to print the dynamic programming table and report the items taken by the thief and their total value.
  • The main method initializes the items available in the store, the maximum weight that can be carried by the thief, and creates an instance of the KnapSack class to solve the problem.

Output

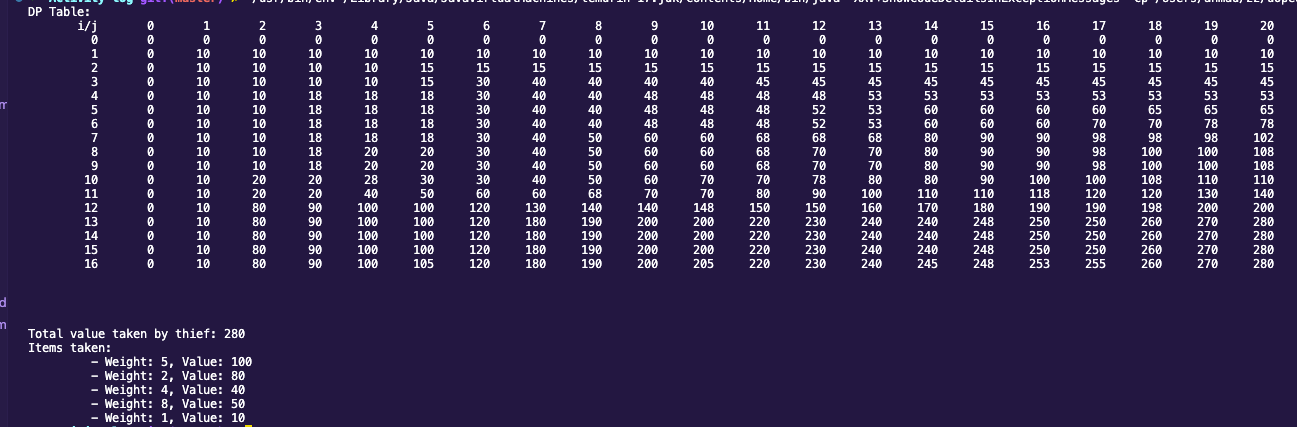
By running the code against the provided input, the following output is generated:

Image 1: Output of the code when run against the provided input.
Image1

And here is the text output:

Total value taken by thief: 280
Items taken:
         - Weight: 5, Value: 100
         - Weight: 2, Value: 80
         - Weight: 4, Value: 40
         - Weight: 8, Value: 50
         - Weight: 1, Value: 10

Below is the table filled by the algorithm according to the method from (Hristakeva & Shrestha, 2005):

Items Capacity 0 1 2 3 4 5 … 13 14 15 16 17 18 19 20
0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0
1 0 10 10 10 10 10 … 10 10 10 10 10 10 10 10
2 0 10 10 10 10 15 … 15 15 15 15 15 15 15 15
3 0 10 10 10 10 15 … 45 45 45 45 45 45 45 45
4 0 10 10 18 18 18 … 53 53 53 53 53 53 53 53
5 0 10 10 18 18 18 … 53 60 60 60 60 65 65 65
6 0 10 10 18 18 18 … 53 60 60 60 70 70 78 78
7 0 10 10 18 18 18 … 68 80 90 90 98 98 98 102
8 0 10 10 18 20 20 … 70 80 90 90 98 100 100 108
9 0 10 10 18 20 20 … 70 80 90 90 98 100 100 108
10 0 10 20 20 28 30 … 80 80 90 100 100 108 110 110
11 0 10 20 20 40 50 … 100 110 110 118 120 120 130 140
12 0 10 80 90 100 100 … 160 170 180 190 190 198 200 200
13 0 10 80 90 100 100 … 240 240 248 250 250 260 270 280
14 0 10 80 90 100 100 … 240 240 248 250 250 260 270 280
15 0 10 80 90 100 100 … 240 240 248 250 250 260 270 280
16 0 10 80 90 100 105 … 240 245 248 253 255 260 270 280

Complexity Analysis

The dynamic programming approach has the advantage of being more efficient than the brute force approach, as it eliminates redundant computations caused by the un-used irrelevant combinations storing and reusing the results of subproblems.

The time complexity of the dynamic programming approach is O(nW), where n is the number of items and W is the weight capacity of the knapsack, making it more practical for larger problem instances. The space complexity is O(nW) to store the two dimensional array that holds the results of the subproblems (Hristakeva & Shrestha, 2005).

This clear from our implementation, as we have two nested loops to fill the dynamic programming table (one loop for the items (n) and one loop for the capacities (W)). The space complexity is also proportional to the number of items and the weight capacity of the knapsack (an array of size n * W). Hence, both time and space complexity are linear and proportional to the number of items and the weight capacity of the knapsack O(nW).

Conclusion

We have provided the source code, source code explanation example output, and asymptotic analysis. Here are our checks for the assignment requirements:

Requirement Achieved ? Comment
Was a java algorithm solution for the knapsack problem provided ? ✅ See the Source code section or the attached java file.
Is the code documented to give the reader ? ✅ Code comments + see code explanation section.
Does the java algorithm execute in the Java IDE environment? ✅ See attached output, and follow instructions to run it yourself.
When executed does the algorithm produce the appropriate output? ✅ Output: value 280. weight 20. stolen items: 5, 2, 4, 8, 1
Does the assignment include an asymptotic analysis ? ✅ See Complexity analysis section. O(nW) for both space and time.

References