DA5. Monopolistic Competition Exercise¶
Statement¶
Suppose that a typical firm in a monopolistically competitive industry faces a demand curve given by:
\(q = 60 − (1/2)p\), where q is quantity sold per week.
The firm’s marginal cost curve is given by: \(MC = 60\).
- How much will the firm produce in the short run?
- What price will it charge?
- In addition to providing the quantitative answers for the question, please also describe the approach you used to arrive at your conclusions.
Answer¶
According to Rittenberg and Tregarthen (2009), the model of monopolistic competition looks exactly like the model of monopoly in the short run. That is, the demand curve is downward-sloping, the marginal revenue curve has double the slope of the demand curve, and the firm will produce according to the marginal decision rule where marginal cost equals marginal revenue.
We will use mathematical calculations and graphs to find the quantity produced and the price charged by the firm; and then summarize the results.
Mathematical Method¶
- The firm will produce where \(MC = MR\).
- Let’s find the marginal revenue curve first, by inverting the demand curve and then duplicating its slope.
And after duplicating the slope: \(MR = 120 - 4q\).
let’s find the quantity where \(MC = MR\):
- The firm will produce 15 units per week.
- Lwt’s find the price by substituting the quantity into the demand curve:
- The firm will charge $90 per unit.
Graph Method¶
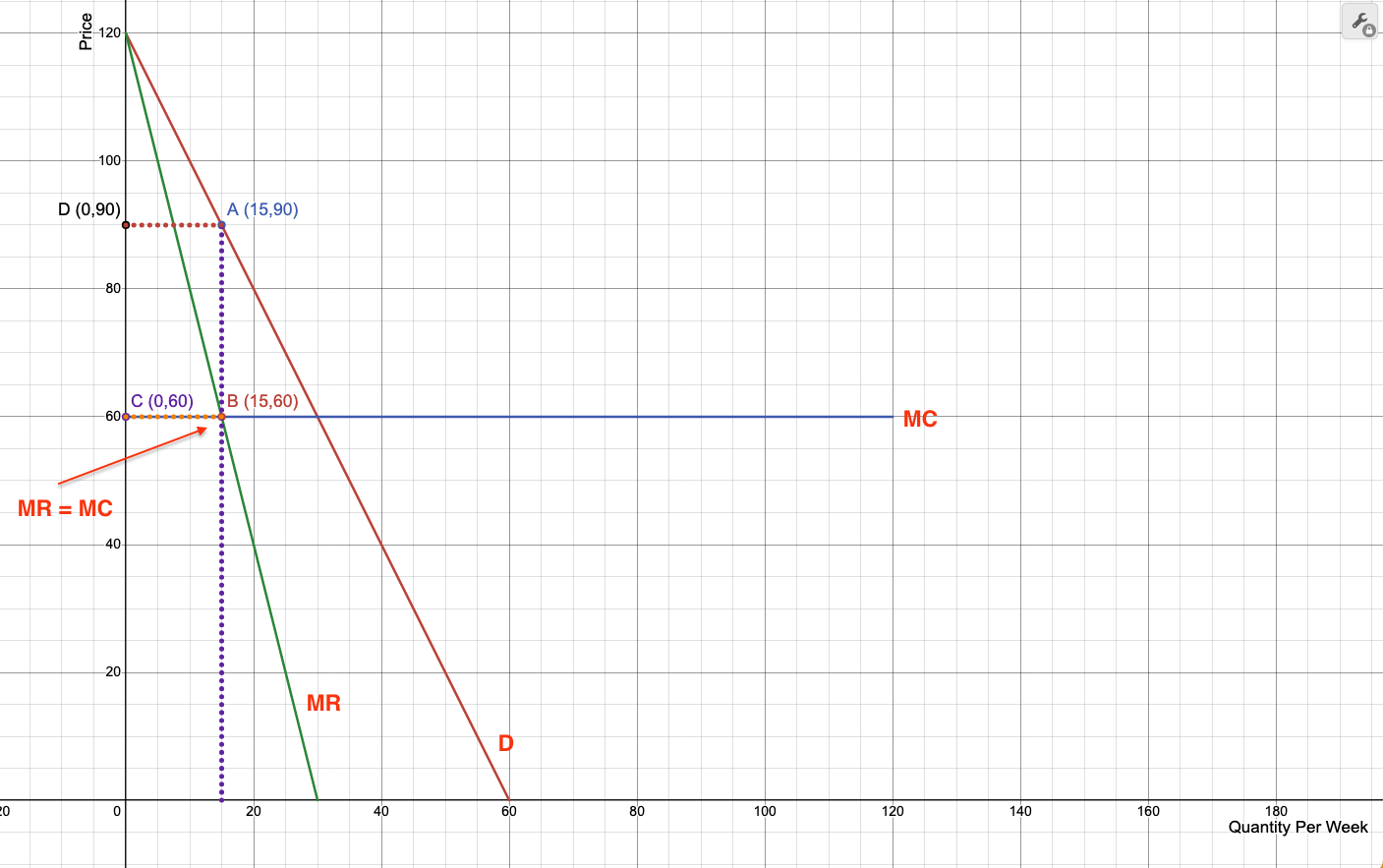
The demand is the red line (D), marginal cost is the blue line (MC), and marginal revenue is the green line (MR). MR intersects MC at point B (15,60). The price is found by intersecting the demand curve with the quantity produced (15), and this happens at point A (15,90).
Summary¶
The firm will produce 15 units per week and charge $90 per unit.
The idea is that at the equilibrium point, the firm will produce where MC=MR, and then charge the price that corresponds to the quantity produced on the demand curve; this gives the firm the highest marginal profit possible which corresponds to the difference between the price and the marginal cost.
There is still a positive marginal profit of 90-60=$30 per unit, which is the highest profit the firm can achieve in the short run. The total profit can be computed using as TP = q * MP = 15 * 30 = 450.
References¶
- Rittenberg, L. & Tregarthen, T. (2009). Principles of Economics. Flat World Knowledge. Chapter 11: The World of Imperfect Competition. <https://my.uopeople.edu/pluginfile.php/1894552/mod_book/chapter/527802/Principles%20Of%20Economics%20Chapter%2011.pdf>