Skip to content

7. Interpolation and Spline Modeling

Introduction 1

  • Linear interpolation: connecting two vertices with a straight line.
  • Anti-aliasing can be used to adjust the position and intensity of some of the pixels within the model to smooth the line.
  • Interpolating a spline is a bit more complex.
  • In the linear model, we are using some variation of the equation of a line to compute the position of pixels that exist between the two vertices.
  • In a spline, we select a series of control points (2 or more), and a curve is fitted within these control points based upon the particular algorithm used.

Bezier Curves and Splines 2

  • PolyLines: a sequence of vertices connected by straight line segments.
  • Smooth curves: a sequence of vertices connected by curves.
  • Splines:
    • A sequence of vertices connected by curves based on a set of control points.
    • A special type of smooth curve in 2D or 3D space.
    • Use cases:
      • 2D illustrations.
      • Fonts.
      • Animation: trajectory of objects.
  • Definitions of Curves:
    • A curve is a continuos 1D set of points in 2D or 3D space.
    • A curve is a mapping from an interval S onto a plane.
  • Two approaches: Interpolation and Approximation:
    • Interpolation goes through all control points, while approximation may skip some.
    • Interpolation is more complex and less stable, while approximation is more convenient.
  • Why interpolation is useful:
    • Good for UI: smooth curves.
    • Good for storage: only store control points.
  • Tessellation:
    • The process of breaking down a curve into a series of straight lines.
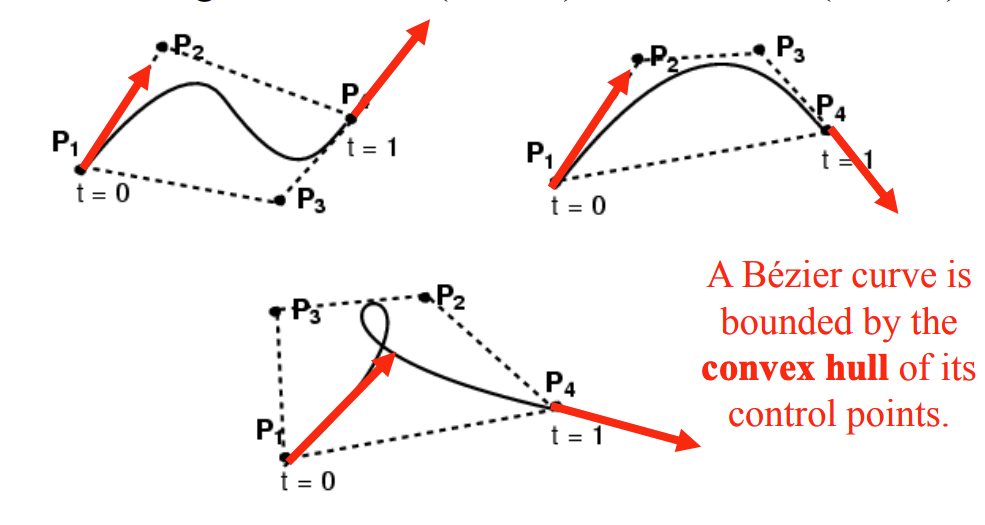
  • Cubic Bézier Curve:
    • It is a curve defined by four control points (P1, P2, P3, P4).
    • The curve starts at P1 and ends at P4.
    • The curve may not pass through P2 and P3.
    • The equation is cubic polynomial.
    • Curve is tangent at P1 to (P1-P2) and at P4 to (P4-P3).
    • Cubic Bezier Curve
    • P(t) is a weighted combination of the 4 control points with weights:
      • \(B1(t) = (1-t)^3\)
      • \(B2(t) = 3t(1-t)^2\)
      • \(B3(t) = 3t^2(1-t)\)
      • \(B4(t) = t^3\)
    • First P is the most influential, as P1 > P2 > P3 > P4 in their influence.
    • The basis polynomials/vectors are Bernstein polynomials (4X1 vectors).
    • \(P(t) = P1B1(t) + P2B2(t) + P3B3(t) + P4B4(t) = \sum_{i=1}^{4} P_iB_i(t)\)
  • Bezier Curves of degree n:
    • \(P(t) = \sum_{i=0}^{n} P_iB_i(t)\)
    • We can find the equation of a Bezier curve of any degree, if we know n, and i according to:
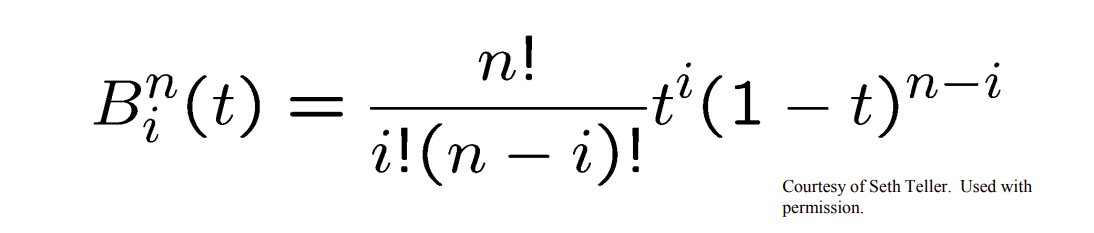
    • Bezier Curves of degree n
    • \(B_i^n(t) = \frac{n!}{i! (n-i)!}t^i(1-t)^{n-1}\)

Curves Properties and Conversion, Surface Representation 2

  • Linear Transformations & Cubics:
    • We transform the control points of a cubic Bezier curve using a linear transformation matrix.
    • Because everything is linear, it is the same as transforming only the control points.
  • Continuity:
  • Parametric surface P(u,v):
    • It is a bicubic polynomial of two variables u & v.
    • Defined by 4x4=16 control points P1,1, P1,2.... P4,4.
    • Basis are product of two Bernstein polynomials: B1(u)B1(v); B1(u)B2(v);… B4(u)B4(v).
    • Interpolates 4 corners, approximates others.
  • It turns out corner cutting (Chaikin’s Algorithm) produces a quadratic BSpline curve.

Interactive Introduction to Splines 3

Bezier Spline Curves

  • Linear Bezier spline:
    • It is a linear interpolation between two points. P0 and P1.
    • \(P(t) = (1-t)P0 + tP1\) for \(0 \leq t \leq 1\).
    • It is a straight line starts at P0 and ends at P1.
  • Quadratic Bezier spline:
    • It is a quadratic interpolation between three points. P0, P1, and P2.
  • Cubic Bezier spline:
    • It is a cubic interpolation between four points. P0, P1, P2, and P3.
    • It is a curve that starts at P0 and ends at P3.

Interpolation and Spline Modeling 4

  • Interpolation:
    • It is a method of constructing new data points within the range of a discrete set of known data points.
    • Example: given a set of a few points that belongs to a curve, we can interpolate the curve to find the points in between.
  • Algorithms of Interpolation:
    • Bernstein, Bezier. and Catmull-Rom.
    • All of them are equations that can be used to interpolate a curve based on some parameters and a set of points.
  • Spline:
    • A spline is a curve that is defined by a set of control points and a set of basis functions that are used to interpolate the curve.
    • It is obtained by DeCasteljau algorithm.

References

‌ ‌

  1. Learning Guide Unit 7: Introduction | Home. (2024). Uopeople.edu. https://my.uopeople.edu/mod/book/view.php?id=444306&chapterid=540625 ↩

  2. Massachusetts Institute of Technology (2020). Coordinates and Transformations. MITOpenCourseware. https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-837-computer-graphics-fall-2012/lecture-notes/. (Original work published 2001). Read Lecture #1: Bezier Curves and Splines. Read Lecture #2: Curves Properties and Conversion, Surface Representation. ↩↩

  3. An Interactive Introduction to Splines. (2021). Ibiblio.org. https://www.ibiblio.org/e-notes/Splines/Intro.htm ↩

  4. Unit 7 Lecture 1: Interpolation and Spline Modeling | Home. (2024). Uopeople.edu. https://my.uopeople.edu/mod/kalvidres/view.php?id=444312 ↩