JA8. Logistic Regression - O-Ring Damage¶

Statement¶

Observational data on O-rings from 23 shuttle missions showing the number of damaged and undamaged O-rings for each space mission is provided here: shuttlemission.csv

For this task, we are interested in modelling the probability of damage to O-ring due to the temperature.

Dependent Variable	Independent Variable
Damaged (damage to the O-ring: 1 for damaged, 0 for undamaged)	Temperature (ambient temperature in degree Fahrenheit)

a. Import the data in JASP and run the logistic regression model on interest (provide a full capture of the output).
b. Write the equation for the logistic regression based on the JASP output.
c. Is the β estimate associated with Temperature statistically significant with a 5% significance level? Interpret.
d. Based on the output of the logistic model, is it justified that a part of the O-rings was damaged because of temperature (Yes/No)? Interpret.
e. Find the model-estimated probability an O-ring being damaged for the following ambient temperatures:

Temperature (°F)	\(\hat{p}\)
51
53
55
57

Answer¶

Regression Analysis Process Using JASP¶

Here is a step-by-step guide on how to perform a logistic regression analysis in JASP (JASP Statistics, 2018):

Convert the data to a CSV file:
- The data is provided as a xlsx file, which is not directly compatible with JASP. We need to convert it to a csv file.
- I opened the file in Excel and saved it as a csv file named shuttlemission.csv.
Load the data into JASP:
- Use File > Open from the top menu.
- Select Computer and then Browse.
- Select the dataset file.
Do the logistic regression analysis:
- From the JASP menu, select Regression and then Logistic Regression.
- Drag the dependent (outcome) variable to the Dependent Variable box.
- Drag the independent (predictor) variable to the Covariates and Factors boxes.
  - For categorical predictors, drag them to the Factors box.
  - For continuous predictors, drag them to the Covariates box.
- Under Statistics > Regression Coefficients, select Odds Ratios to get the odds ratios for the predictors.
- Under Plots, select Display conditional estimates plot to get the predicted probabilities for the predictors.
- Under Statistics:
  - From Performance Diagnostics, select Confusion Matrix to get the confusion matrix.
  - From Performance metrics:
    - Select Sensitivity which describes the proportion of true positives.
    - Select Specificity which describes the proportion of true negatives.

Results of the Analysis¶

We have loaded the data into JASP and performed the logistic regression analysis. The results are as follows:

Image 1: Logistic Regression Output

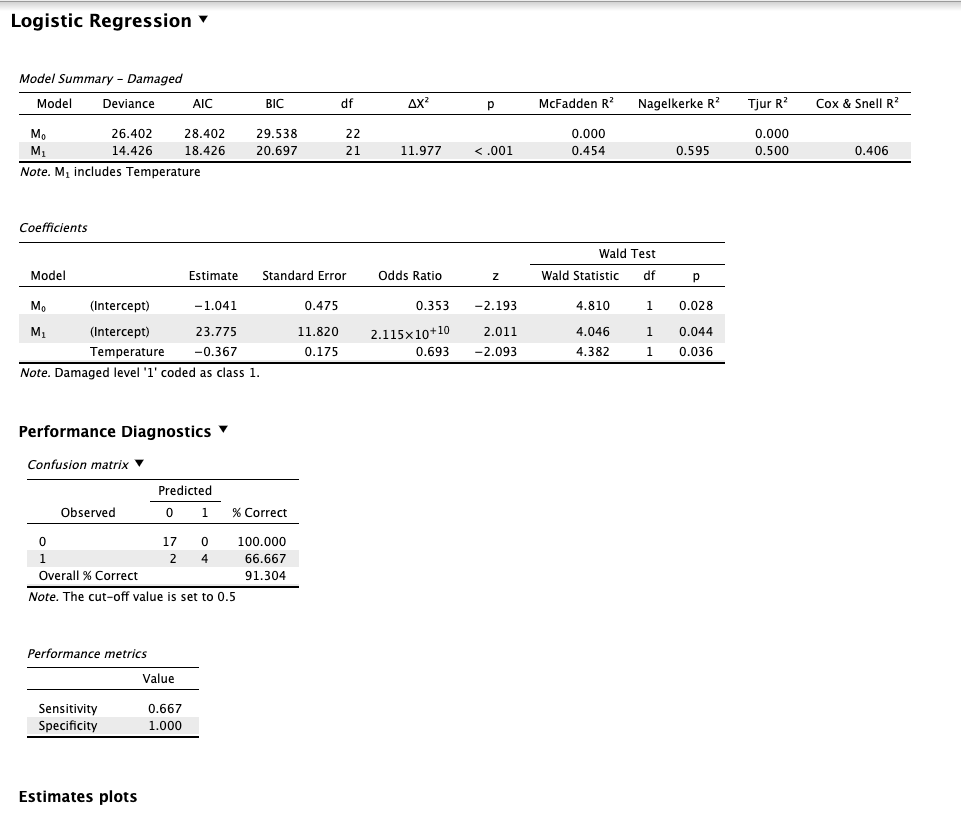Image 2: Logistic Regression Output (2)

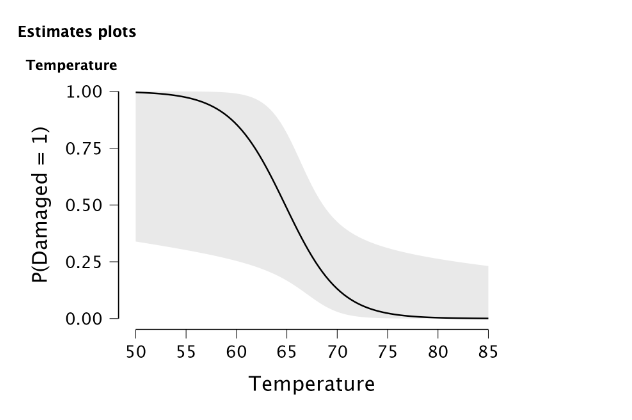A. Import the data in JASP and run the logistic regression model on interest (provide a full capture of the output)¶

The logistic regression model was run in JASP with the dependent variable Damaged and the independent variable Temperature. The output of the logistic regression analysis is shown in the images (Image 1 and Image 2) above.

B. Write the equation for the logistic regression based on the JASP output¶

Looking at the coefficients table in the output, shown in the Image 3 below:

Image 3: Coefficients Table

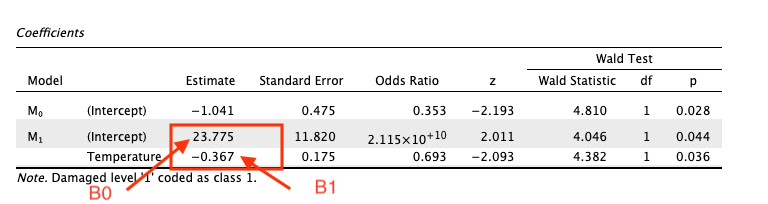The general form of the regression equation is:

\[ \begin{align*} \text{logit}(p) = \beta_0 + \beta_1 \times \text{Temperature} \\ = 23.775 - 0.367 \times \text{Temperature} \end{align*} \]

Where:

\(\beta_0 = 23.775\) which is the intercept estimate of the model (M1).
\(\beta_1 = -0.367\) which is the coefficient estimate of the Temperature variable.

C. Is the β estimate associated with Temperature statistically significant with a 5% significance level? Interpret¶

Looking at the coefficients table in the output, shown in the Image 4 below:

Image 4: Coefficients Table

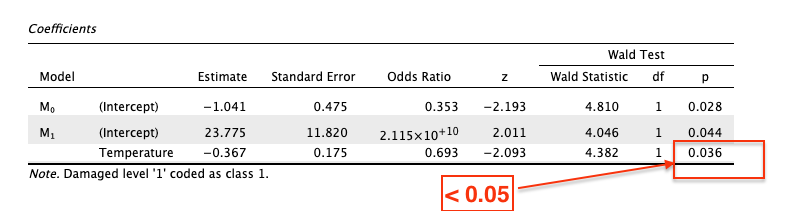The p-value associated with the Temperature variable is 0.036. Since this p-value is less than the significance level of 0.05, we can conclude that the coefficient estimate \(\beta_1\) associated with Temperature is statistically significant at the 5% significance level.

D. Based on the output of the logistic model, is it justified that a part of the O-rings was damaged because of temperature (Yes/No)? Interpret¶

Based on the previous question, we can conclude that there is a statistically significant negatively correlated relationship between the Temperature and the probability of an O-ring being damaged. But as the coefficient is negative, it implies that as the Temperature increases, the probability of O-ring being damaged decreases (response variable is 1). Therefore, it is not justified to say that a part of the O-rings was damaged because of temperature, but rather the opposite.

E. Find the model-estimated probability an O-ring being damaged for the following ambient temperatures¶

\[ \begin{align*} logit(p) &= 23.775 - 0.367 \times \text{t} \\ log(\frac{\hat{p}}{1 - \hat{p}}) &= 23.775 - 0.367 \times \text{t} \\ \frac{\hat{p}}{1 - \hat{p}} &= e^{23.775 - 0.367 \times \text{t}} \\ \hat{p} &= (e^{23.775 - 0.367 \times \text{t}}) \times (1 - \hat{p}) \\ \hat{p} &= (e^{23.775 - 0.367 \times \text{t}}) - \hat{p} (e^{23.775 - 0.367 \times \text{t}}) \\ \hat{p} + \hat{p} (e^{23.775 - 0.367 \times \text{t}}) &= (e^{23.775 - 0.367 \times \text{t}}) \\ \hat{p} (1 + e^{23.775 - 0.367 \times \text{t}}) &= (e^{23.775 - 0.367 \times \text{t}}) \\ \hat{p} &= \frac{e^{23.775 - 0.367 \times \text{t}}}{1 + e^{23.775 - 0.367 \times \text{t}}} \end{align*} \]

And we can use the final equation to calculate the estimated probability of an O-ring being damaged for the given temperatures:

Temperature (°F)	\(\hat{p}\)
51	0.994
53	0.987
55	0.973
57	0.945

Notice that as the temperature increases, the probability of an O-ring being damaged decreases which confirms our answer to question D.

References¶

JASP Statistics. (2018, February 11). How to perform a logistic regression analysis in JASP [Video]. YouTube. https://youtu.be/bUgpJeeReBY