JA6. Partial Ordering and Mathematical Induction¶
Task 1¶
Explain what a partial ordering relation is by taking an example of one of the three relations: subset (\(\subseteq\)) , divides (\(|\)), and less than or equal to ( \(\leq\) ) on a set containing at least three elements of your choice. Draw a Hasse diagram of the relation using MS Word, a hand-drawn image, or the graph online tool. Explain the Hasse diagram
- Let’s take the set \(S = \{1,2,3,4\}\) and the relation \(R = \{(a,b) \in S | a \text{ divides } b\}\).
- The Relation will include: \(\{(1,1),(1,2),(1,3),(1,4),(2,2),(2,4),(3,3),(4,4)\}\).
- Partial ordering requires the relation R on set S to be, reflexive, antisymmetric, and transitive (Neso Academy, 2022).
Let’s discuss each one of these properties:
- Reflexive:
- For each element
ain the setS, the pair(a,a)is in the relation. - We notice that for every element in R, the pair
(a,a)is in the relation; that is, the pairs(1,1),(2,2),(3,3),(4,4)are in the relation. - Thus, the relation is reflexive.
- For each element
- Antisymmetric:
- For each pair
(a,b)in the relation, the pair(b,a)is not in the relation unlessa=b. - Let’s exclude the pairs where
a=bfrom the relation, we’ll get the following pairs: \(\{(1,2),(1,3),(1,4),(1,5),(2,4)\}\). - Foe each one of these pairs, the pair
(b,a)should not be in the relation; that is, the following pairs(2,1),(3,1),(4,1),(5,1),(4,2)should not be in the relation and we can confirm that. - Thus, the relation is antisymmetric.
- For each pair
- Transitive:
- If the pair
(a,b)and the pair(b,c)are in the relation, then the pair(a,c)is also in the relation. - Let’s take the following pairs from the relation: \(\{(1,2),(2,4)\}\), we notice that the pair
(1,4)is in the relation. - We can continue the reasoning for all the pairs in the relation and we’ll find that the relation is transitive.
- If the pair
By the discussion above, we have proven that the relation R is reflexive, antisymmetric, and transitive; thus, it is an partial ordering relation.
Note: we can prove using general example, but the way used above is sufficient for the given task.
- The diagram:
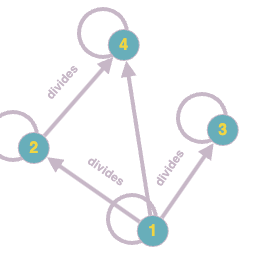
Notice the edges are directed from the divisor to the dividend, and the states the word “divides” on the edge. For elements that divides itself, we draw a circle around the number.
Task 2¶
(i) What is Transitive closure of relations. Where is it used? Explain with an example.
According to (Doerr & Levasseur, 2022), the transitive closure of a relation \(R\) on a set \(S\) is the smallest transitive relation \(R^+\) on \(S\) that contains \(R\) as a subset.
Let’s take an example: Let S={1,2,3,4} and R={(a,b) ∈ S | a<b }, thus, the relation R will contain the following paris:
We can use the definition of the transitive closure to find the transitive closure of the relation R:
We notice that R is not transitive, however, R+ is transitive.
(ii) Consider the relation R defined on the set of integers as R = {(x,y): x,y \(\in\) ℤ, (x-y) is a multiple of 11}. Show that R is an equivalence relation.
For a relation to be an equivalence relation, it should be reflexive, symmetric, and transitive.
- Reflexive:
- For each element
ain the setS, the pair(a,a)is in the relation. - For any integer
a,(a-a)is a multiple of 11, asa-a=0, and0*11=0; thus 0 is a multiple of 11, and the pair(a,a)is in the relation. - Thus, the relation is reflexive.
- For each element
- Symmetric:
- For each pair
(a,b)in the relation, the pair(b,a)is also in the relation. - If
(a,b)is in the relation, then(a-b)is a multiple of 11. - Then,
(b-a)is also a multiple of 11, as(b-a) = -(a-b). - Thus, the relation is symmetric.
- For each pair
-
Transitive:
- If the pair
(a,b)and the pair(b,c)are in the relation, then the pair(a,c)is also in the relation. - If
(a,b)is in the relation, then(a-b)is a multiple of 11, and if(b,c)is in the relation, then(b-c)is a multiple of 11. - In the case where
a=b=c, then(a-c)is a multiple of 11, as(a-c) = 0, and0*11=0. - If
a≠b≠c, then(a-c)is a multiple of 11, as(a-c) = (a-b) + (b-c), and the sum of two multiples of 11 is a multiple of 11. - Thus, the relation is transitive.
- If the pair
-
(a) Find the equivalence class of 0 for the relation R
- (b) Calculate the number of equivalence classes for the relation R.
The possible remainders of the division of an integer by 11 are: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10. Thus, there are 11 equivalence classes for the relation R.
Task 3¶
Prove 5n > 4n for n≥ 1 using Mathematical induction.
Let’s prove the statement for \(n=1\) (base case): \(5(1) > 4(1) ⟹ 5 > 4\), thus the statement is true for \(n=1\).
Let’s assume that the statement is true for \(n=k: k>1\) (inductive hypothesis)
And prove that it is true for \(n=k+1: k>1\) (inductive step):
Thus the statement is true for \(n=k+1\), and then it is true for all \(n≥1\).
Task 4¶
Let A be a set of five integers of your choice. Establish a relation R = ‘≥’ (greater than or equal to) on A. For this relation (≥):
Let \(A = \{1,2,3,4,5\}\) and \(R = \{(a,b) \in A | a \geq b\}\)
The Relation R will include the following pairs:
- (i) Draw the diagrammatical representation R on A
- (ii) Find an adjacency matrix R on A
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 |
| 3 | 1 | 1 | 1 | 0 | 0 |
| 4 | 1 | 1 | 1 | 1 | 0 |
| 5 | 1 | 1 | 1 | 1 | 1 |
- (iii) Draw the Hasse diagram R on A
References¶
- Doerr, A., & Levasseur, K. (2022). Applied discrete structures (3rd ed.). licensed under CC BY-NC-SA. https://discretemath.org/ads/chapter_7.html.

