DA1. Understanding Confidence Intervals¶
Statement¶
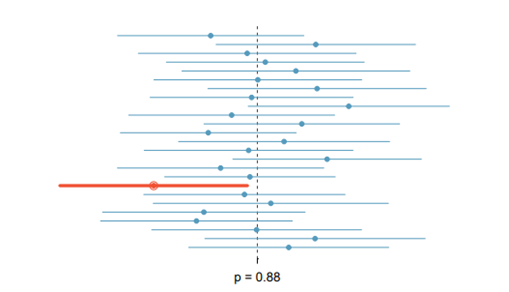
- The graph shows the simulation of 25 intervals from 25 samples proportions with a 95% confidence level. One interval missed the population parameter (p=0.88)
- a) What is the formula for the confidence interval for a sample proportion?
- b) What parameters of the formula above can you modify to ensure that the confidence interval captures the population parameter?
- List the conditions necessary for the CLT to hold. Make sure to list alternative conditions for when we know the population distribution is normal vs. when we do not know what the population distribution is; and then when the sample size is barely over 30 vs. when it’s very large.
- Explain in your own words, the difference between standard error and margin of error.
Answer¶
Question 1 - A¶
According to Diez, Barr, and Çetinkaya-Rundel (2019, p.181), the formula for the confidence interval for a sample proportion is:
Where:
- \(\text{point estimate}\) is the sample proportion, and usually denoted as \(\hat{p}\).
- \(z^*\) is the critical value for the confidence level. It usually corresponds to the z-score for the desired confidence level, and equals 1.96 for a 95% confidence level.
- \(\text{standard error}\) is the standard error due to the randomness in the sampling process, and is calculated as \(\sqrt{\frac{p(1-p)}{n}}\).
- \(n\) is the sample size.
Thus the final formula for the confidence interval for a sample proportion is:
Question 1 - B¶
To ensure that the confidence interval captures the population parameter, assuming that we can not change the confidence level; that leaves us with the sample size \(n\) as the only parameter we can modify.
The larger the sample size, the smaller the standard error, and as the sample size approaches population size, the sample proportion approaches the population proportion.
If we can raise the confidence level, then then the confidence interval will be wider, and it will capture more of the possible values of the population parameter. Though, 95% confidence level is widely accepted in statistics.
Question 2¶
According to Diez, Barr, and Çetinkaya-Rundel (2019, p.175), the conditions necessary for the Central Limit Theorem (CLT) to hold are:
- The observations are independent.
- The success-failure condition:
- \(np > 10\).
- \(n(1-p) > 10\).
The independence condition depends on the sampling process, and a simple random sample almost ensures that observations do not influence each other; thus, this condition is satisfied in most cases.
The success-failure condition ensures that the sample proportion is a good estimate of the population proportion and it usually depends on the sample size.
If the success-failure condition is met, then the sampling distribution of the parameter estimate will follow a normal distribution, and then we can use the plug-in principle to plug in the sample point estimate in place of the population parameter.
If the success-failure condition is not met, then the sampling distribution may follow a different distribution, where it is hard to infer information about other samples or the population, in other words, the sample only represents itself.
For a sample size less than 30, say 10, let’s evaluate the success-failure condition using \(p=0.88\):
- \(np = 10 \times 0.88 = 8.8 < 10\).
- \(n(1-p) = 10 \times{(1-0.88)} = 10 \times{0.12} = 1.2 < 10\).
Thus, the success-failure condition is not met, and the CLT does not hold.
Let’s evaluate the success-failure condition for a sample size of 30:
- \(np = 30 \times 0.88 = 26.4 > 10\).
- \(n(1-p) = 30 \times{(1-0.88)} = 30 \times{0.12} = 3.6 < 10\).
One of two conditions is met, which is not enough to ensure that the CLT holds; but we are close to meeting the conditions and \(n=84\) is the first sample size that meets both conditions.
Question 3¶
Standard error is the standard deviation of the sampling distribution, and it limits the range of values that the population parameter is likely to take based on the sample point estimate. This error is due to the randomness in the sampling process.
However, multiplying the standard error with the \(z^*\) gives us the margin of error, and it measures by how much the point estimate of the sample varies from the true population parameter.
References¶
- Diez, D. M., Barr, C. D., & Çetinkaya-Rundel, M. (2019). Openintro statistics - Fourth edition. Open Textbook Library. https://www.biostat.jhsph.edu/~iruczins/teaching/books/2019.openintro.statistics.pdf