WA4. Constraint Satisfaction Problem (CSP) Algorithm¶
Statement¶
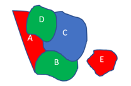
| Image 1: Map of a country with 5 districts | Image 2: Graph representation of Fig 1 map |
|---|---|
 |
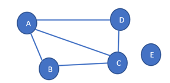 |
Consider the famous map coloring problem. Your goal is to find the minimum number of colors and the color name for the entire map such that two adjacent regions of the map are not colored with the same color. For example, in Fig 1, we need a minimum of 3 colors (red, green, blue).
For this programming assignment, you need to write a program in Java or Python using the Constraint Satisfaction Problem (CSP) algorithm. Here are the detailed requirements.
- Your program must be complete, compile able, and produce output.
- Your program must be generic enough to solve problems with other country maps.
- Your program should be able to handle a minimum of 2 and a maximum of 20 vertices/districts. 2 =< V >= 20, where V is total number of vertices.
- The total number of colors you can use is 7. Red, Green, Blue, Yellow, Violet, Gray, Orange. Remember, your goal is to choose the minimum number of colors. For example, given in Fig 1, you only need 3 colors to satisfy the goal (no adjacent regions has the same color)
- Your program will read the graph from a text file (example: graph.txt)
- Follow the order of the color mentioned in number 4. For example, if you need 4th color, pick Yellow, if you need 5th color, then pick Violet and so on. This would be easier for you when you are assessing your peer’s assignment by comparing it with your output.
- You must follow the CSP backtracking algorithm.
- If your program can’t solve the problem using 7 colors, it should output “Not Possible with 7 colors.”
Sample Input (graph.txt) (Based on Fig 1):
5
A B C D
B A C
C A B D
D A C
E
- The first line represents the total number of vertices/nodes/districts. In this case, the total number is 5.
- After that, there will be the same number of lines representing the vertex name and their adjacent vertices. Each vertex and it’s adjacent must be separated by space. For example, A B C D means vertex A has 3 adjacent vertices which are B, C, and D. The last line represents the vertex E with no adjacent.
Sample Output:
A red
B green
C blue
D green
E red
- Your output should mention each vertex name in a separate line and the appropriate color name separated by one space.
- If a given map is not possible to color with the given 7 colors, simple output the following line:
Not possible with 7 colors
You will be graded on the following:
- Does the program compile?
- Does the program correctly read the input file?
- Does the data structure correctly represent the map/graph?
- Is the Constraint Satisfaction Problem (CSP) backtracking algorithm correctly implemented?
- Does the program produce the correct output?
- Do you think given a scenario where 7 colors are not enough to solve the problem, the program will give the corresponding output?