Skip to content

8. Logistic Regression

Multiple and Logistic Regression 1

  • 4 conditions for logistic regression:
    • (1)- Residuals are nearly normal.
    • (2)- Variability of residuals is nearly constant.
    • (3)- Residuals are independent.
    • (4)- Each variable is linearly related to the outcome.
  • Diagnostic plots are used to check these conditions.
(1)- Check for outliers (normality) Histogram of residuals 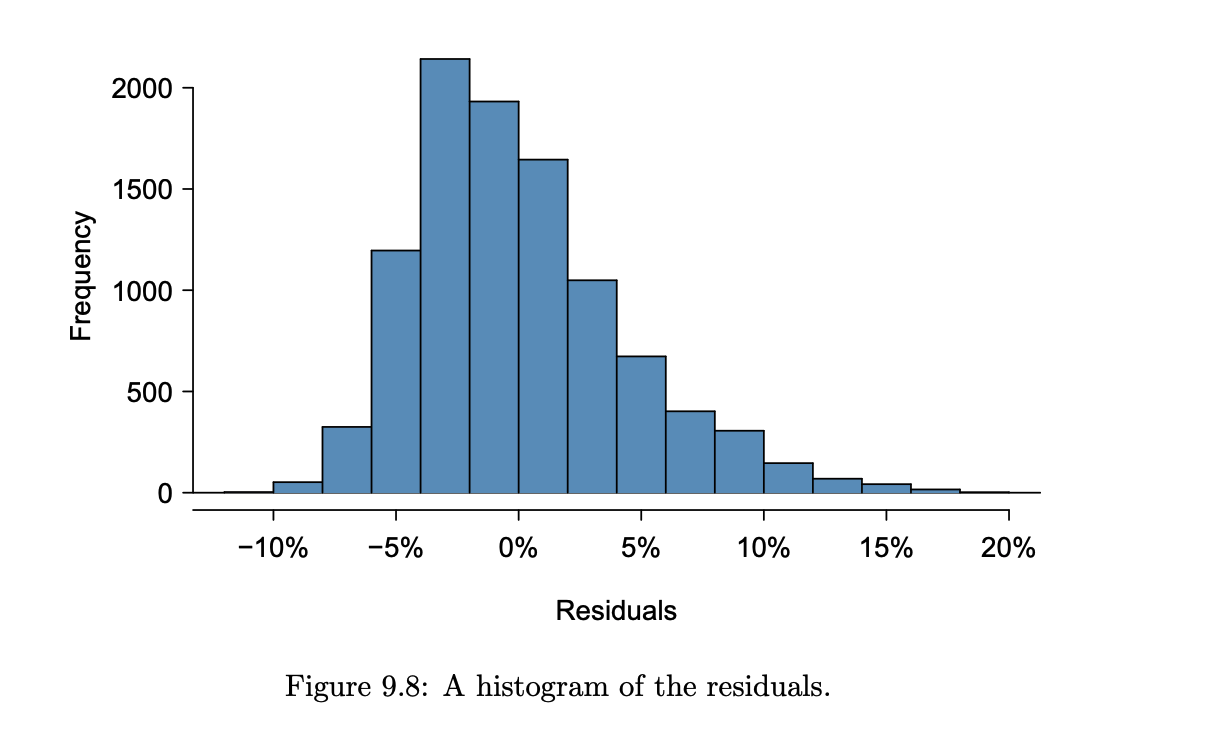histogram
(2)- Check variance of residuals is constant Absolute values of the residuals against fitted (predicted) values 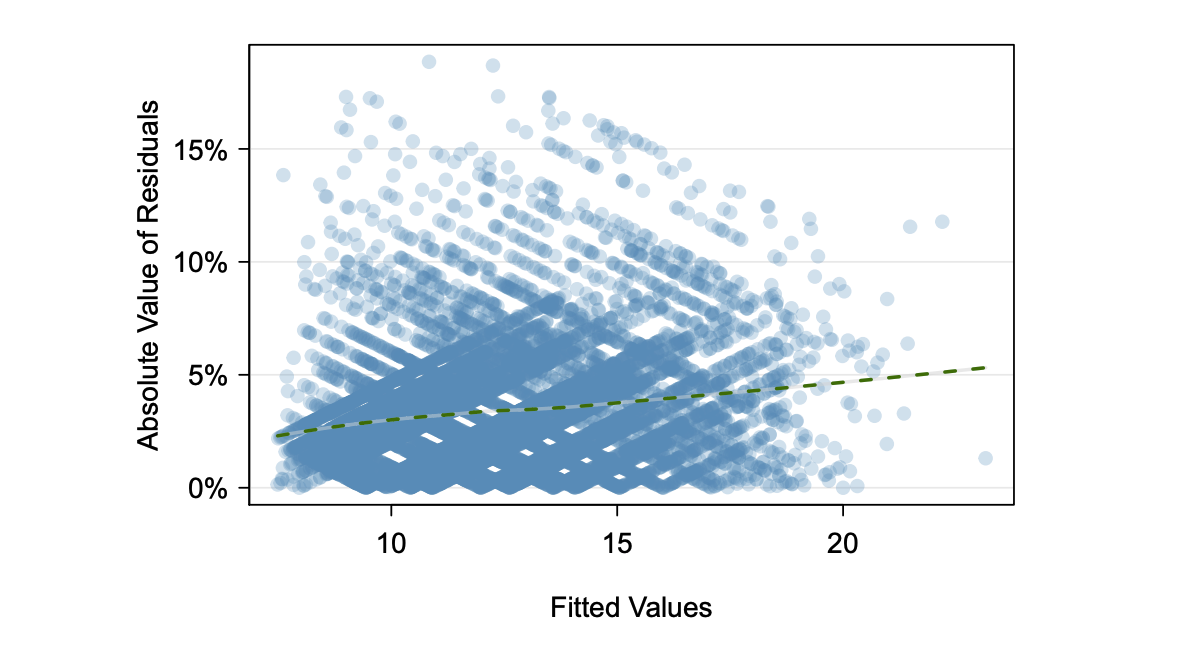residuals/fitted values
(3)- Check No patterns in residuals. Residuals in order of their data collection or Time series
(4)- Check linearity in relation to outcome Residuals against each predictor variable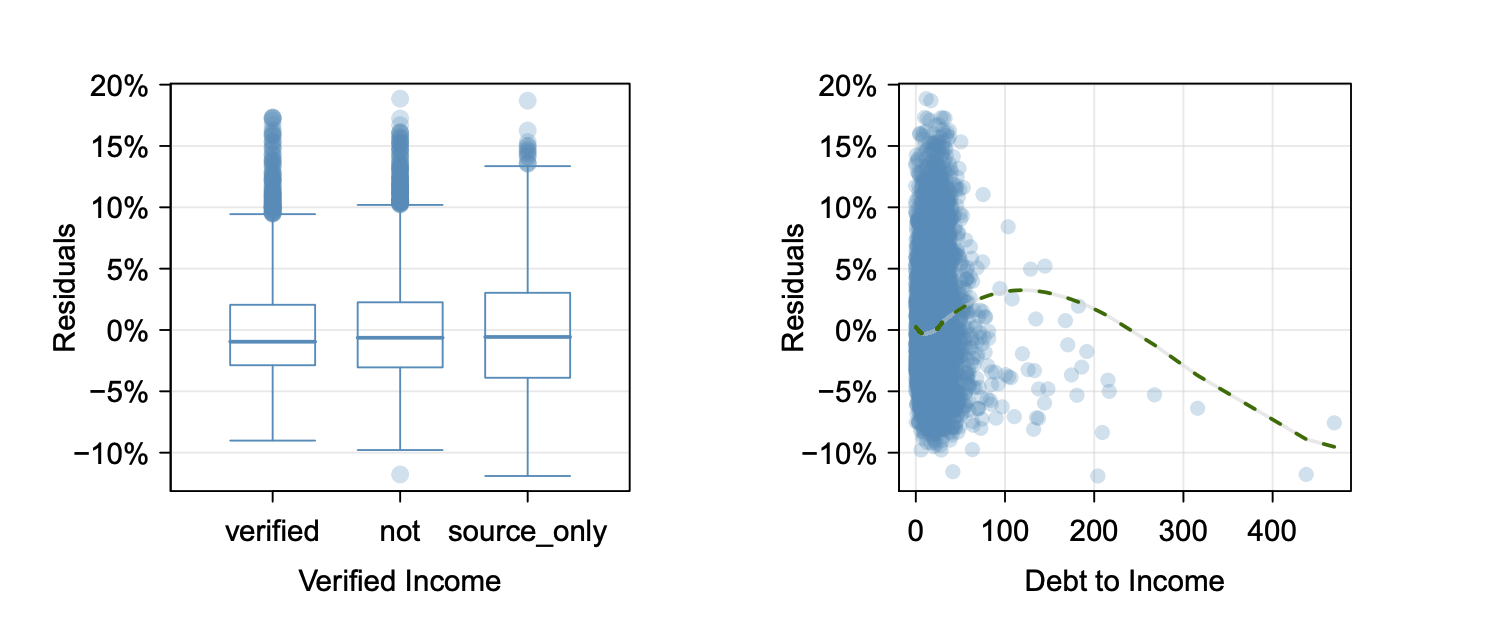

Logistic Regression in JASP 2

  • The null hypothesis tested is that there is no relationship between the outcome and the predictor variable(s).
  • sigmoidal logistic regression curve is fitted with a minimum of 0 and a maximum of 1.
  • The confusion matrix is a table showing actual vs predicted outcomes and can be used to determine the accuracy of the model. From this sensitivity and specificity can be derived.
  • Sensitivity is the percentage of cases that had the observed outcome was correctly predicted by the model (i.e., true positives).
  • Specificity is the percentage of observations that were also correctly predicted as not having the observed outcome (i.e., true negatives).

Checking model conditions using graphs 3

  • Assumptions of logistic regression:
    • Residuals of the model are nearly normally distributed.
    • variability of the residuals is nearly constant across all values of the predictor variable.
    • Residuals are independent of each other.
    • Each variable is linearly related to the outcome.

Basic ideas of logistic regression 4

  • It is used when the outcome variable is binary.
  • It is a type of generalized linear model (GLM) where regular multiple regression does not work.
  • The result takes two possible values, 0 or 1; with \(p_i\) being the probability of the outcome being 1; Hence:
    • The probability of the outcome being 1 is \(p_i\).
    • The probability of the outcome being 0 is \(1 - p_i\).
\[ \begin{align*} transformation(p_i) &= \beta_0 + \beta_1x_{1,i} + \beta_2x_{2,i} + \ldots + \beta_kx_{k,i} \\ logit(p_i) &= log_e(\frac{p_i}{1-p_i}) \end{align*} \]
  • Two key conditions for fitting a logistic regression model:
    • The model relating the parameter \(p_i\) to the predictors \(x_{1,i}, x_{2,i}, \ldots, x_{k,i}\) must closely resemble the true relationship between the predictors and the parameter.
    • The outcome for each case must be independent of the outcome for all other cases.
  • Evaluate the independence assumption by examining the residuals for patterns:
    • \(e_i = Y_i - \hat{p}_i\)

How to perform a logistic regression analysis in JASP 5

  • From the JASP menu, select Regression and then Logistic Regression.
  • Drag the dependent (outcome) variable to the Dependent Variable box.
  • Drag the independent (predictor) variable to the Covariates and Factors boxes.
    • For categorical predictors, drag them to the Factors box.
    • For continuous predictors, drag them to the Covariates box.
  • Under Statistics > Regression Coefficients, select Odds Ratios to get the odds ratios for the predictors.
  • Under Plots, select Display conditional estimates plot to get the predicted probabilities for the predictors.
  • Under Statistics:
    • From Performance Diagnostics, select Confusion Matrix to get the confusion matrix.
    • From Performance metrics:
      • Select Sensitivity which describes the proportion of true positives.
      • Select Specificity which describes the proportion of true negatives.

References

  1. Diez, D. M., Barr, C. D., & Çetinkaya-Rundel, M. (2019). Openintro statistics - Fourth edition. Open Textbook Library. https://www.biostat.jhsph.edu/~iruczins/teaching/books/2019.openintro.statistics.pdf Read Chapter 9 - Multiple and logistic regression Section 9.3 - Checking model conditions using graphs from page 358 to 364 Section 9.5 – Introduction to logistic regression from page 371 to 383 Solve the following practice exercises as homework from the attached: Practice Exercises Unit 8.pdf ↩

  2. Goss-Sampson, M. A. (2022). Statistical analysis in JASP: A guide for students (5th ed., JASP v0.16.1 2022). https://jasp-stats.org/wp-content/uploads/2022/04/Statistical-Analysis-in-JASP-A-Students-Guide-v16.pdf Read Logistic Regression from page 86 to 90. ↩

  3. OpenIntroOrg. (2013a, November 24). Checking multiple regression diagnostics using graphs [Video]. YouTube. https://youtu.be/3KSUeYMKt5A ↩

  4. OpenIntroOrg. (2013b, November 30). Basic ideas of logistic regression [Video]. YouTube. https://youtu.be/uYC2eLVSpI8 ↩

  5. JASP Statistics. (2018, February 11). How to perform a logistic regression analysis in JASP [Video]. YouTube. https://youtu.be/bUgpJeeReBY ↩