Skip to content

DA7. Graph Theory 1

Purpose of this assignment

This assignment will help you develop your understanding of graph theory. The graph theory concepts are essential in many fields, including computer science, mathematics, and engineering, and can help you become a more effective problem solver in your personal and professional life. We encourage you to engage in meaningful discussions with your peers and instructors to deepen your understanding of these concepts.

Assignment Brief

  • In this assignment, we will explore the fundamental concepts of Graph Theory and their applications.
  • Many problems in life may appear different but have the same underlying structure, allowing the same solution to be applied.

Task 1

Explain the concept of isomorphism in discrete mathematics.

Isomorphic graphs are multiple forms of the same graph, that is, all isomorphic graphs have the same number of vertices, edges, and same connections between vertices. The only difference is hiw the graph is drawn (JavaPoint, n.d.).

Another definition states that two graphs \(G1(V1, E1)\) and \(G2(V2, E2)\) are isomorphic if there is bijection \(f: V1 \rightarrow V2\) such that \((u, v) \in E1\) if and only if \((f(u), f(v)) \in E2\) (Morris, 2023).

Thus isomorphism preserves edges and non-edges, that is, the relation on the graph is isomorphic if its an equivalence relation (Morris, 2023) that satisfies the following: Reflexive,Symmetric, and Transitive.

Task 2

Answer the following questions about the two graphs below:

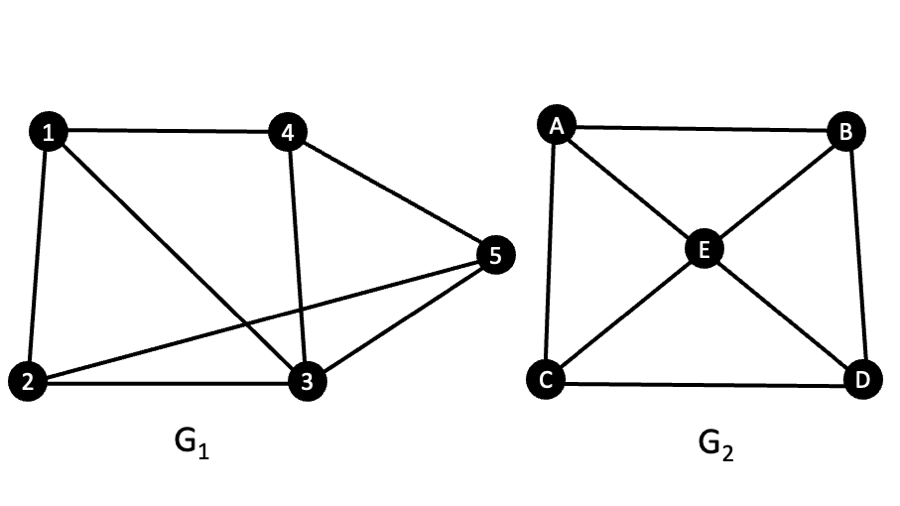
graph

a. Explain in detail how you check isomorphism for the two graphs.

Well, there are various methods to check for isomorphism, I’ll list a couple of them:

First method is to treat each graph as a relation set on that graph, that is every edge relates to every element that its edge connects to. Then, we check if the relation is an equivalence relation. If it is, then the graphs are isomorphic.

Second method is to check if the graphs have the same number of vertices and edges. If they do, then we can check if the graphs have the same degree sequence. If they do, then the graphs are isomorphic.

b. Discuss the conditions of isomorphism for the two graphs in detail.

  • Both graphs have the same number of vertices (5) and edges (8)

  • Let’s check each Vertex of each graph and see its number of edges:

    Graph Vertex Degree Equivalent Vertex From Other Graph
    G1 1 3 A
    G1 2 3 C
    G1 3 4 E
    G1 4 3 B
    G1 5 3 D
    Graph Vertex Degree Equivalent Vertex From Other Graph
    G2 A 3 1
    G2 C 3 2
    G2 D 3 5
    G2 B 3 4
    G2 E 4 3

  • Let’s build the degree sequences for both graphs:

    Graph Degree Sequence
    G1 4, 3, 3, 3, 3
    G2 4, 3, 3, 3, 3

  • The Equivalent Vertex From Other Graph is not necessary, but you can follow it to see how the vertices are connected in both graphs; and it may be needed if you want to follow the first method mentioned in the previous answer.

c. Are these two graphs G1 and G2 isomorphic?

In the previous question we proved that the graphs are isomorphic because they have the same number of vertices, edges, and degree sequence.

References