Skip to content

DA3. Graph Traversals

Statement

Describe and compare both the depth-first and breadth-first search as a graph traversal. As part of your discussion, describe under what conditions or which problem each is best utilized to solve. Finally, your discussion must incorporate a description of how such traversals are implemented as greedy algorithms.

Include one or two examples to explain your thought process to show what is occurring and how the methodology works. Use APA citations and references for any sources used.

Answer

Introduction

Graph is a data structure that consists of nodes and edges that connect those nodes, and it covers some common data structures like trees. Graphs are useful to represent many real-world problems, such as social networks, maps, and networks. Graph traversal is the process of visiting all the nodes in a graph in a specific order (Poole & Mackworth, 2017).

There are two common methods to traverse a graph: depth-first search (DFS) and breadth-first search (BFS), which are both examples of greedy algorithms; but they differ by the way they select the pool of nodes (frontier) to visit next. The text will discuss DFS and BFS separately, compare them using bus traveling example, and conclude with a summary of both methods.

Depth-First Search (DFS)

Depth-first search (DFS) is a graph traversal algorithm that explores a branch (or a single path) as far as possible before backtracking to the adjacent paths. It uses a stack to build its frontier and then pops the last added node until the stack is empty. In other words, DFS will recursively visit all nodes unvisited neighbors before moving to the next node (Shaffer, 2011).

DFS can be implemented as a greedy algorithm by recursively selecting the left most child of a node until it reaches a leaf; where it backtracks one parent at a time visiting the next right child, until it goes back to the root node. DFS is more useful if we think solutions are very deep (far away) from the root (or the starting node).

Breadth-First Search (BFS)

Breadth-first search (BFS) is a graph traversal algorithm that explores all the nodes at the current depth (level) before moving to the next depth. It uses a queue to build its frontier and then dequeues the first added node until the queue is empty.In other words, BFS will visit all the nodes connected to the current node before moving to the next node (Shaffer, 2011).

BFS can be implemented as a greedy algorithm by selecting all nodes connected to the current node before moving to the next node. BFS is more useful if we think solutions are shallow or if we need to explore possible paths horizontally.

Comparison of DFS and BFS

In an imagery example of traveling between train station T1 and T2 using buses. There are three bus routes leaves from T1 which are B1, B2, and B3, but none of them goes directly to T2; instead, they connect to B4, B5, and B6 respectively. Imagine that we want to travel from T1 to T2 using all routes; that is, we need to ride all buses at least once.

In the DFS traversal, we would start from B1->B4->T2, then backtrack to B2->B5->T2, and finally B3->B6->T2. In the BFS traversal, we would start from B1->B2->B3, then B4->B5->B6, and finally T2. The images below show the traversal of the bus routes using DFS and BFS.

Image 1: DFS Traversal
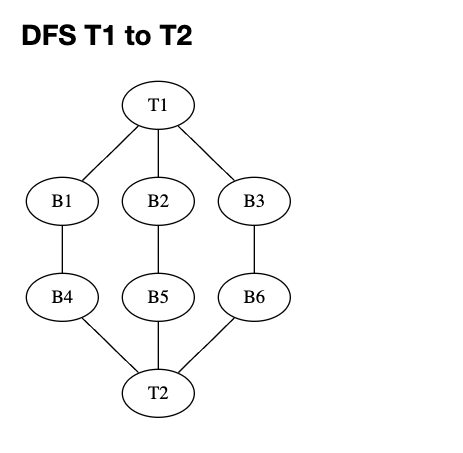DFS Traversal
Image 2: BFS Traversal
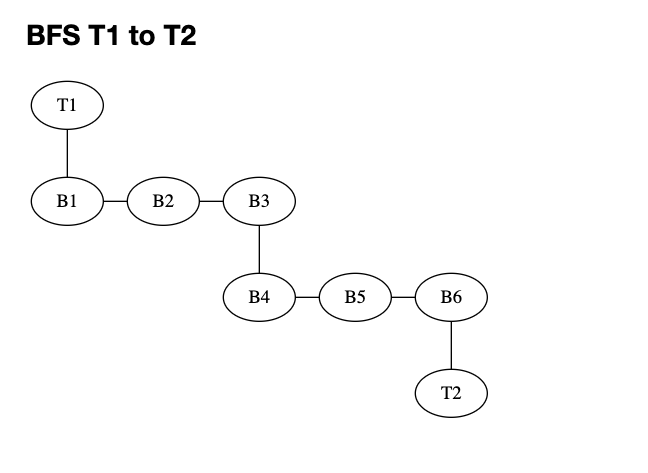BFS Traversal

Conclusion

To conclude, notice the difference in the generated paths between the two methods, where DFS seems to go up and down, while BFS goes horizontally level by level. Both methods are greedy algorithms that make the best choice at each step without worrying about the future or the overall cost with DFS more useful if we think the solutions are very deep from the root, while BFS is more useful if we think solutions are shallow.

References