DA1. The Maximum value of a function

Statement

In many areas of science, engineering, and mathematics, it is useful to know the maximum value a function can obtain, even if we don’t know its exact value at a given instant. For example, if we have a function describing the strength of a roof beam, we would want to know the maximum weight the beam can support without breaking. If we have a function that describes the speed of a train, we would want to know its maximum speed before it jumps off the rails. Safe design often depends on knowing maximum values. This project describes a simple example of a function with a maximum value that depends on two-equation coefficients. We will see that maximum values can depend on several factors other than the independent variable x.

1. Consider the graph of the function y = sin x + cos x. Describe its overall shape. Is it periodic? How do you know?
2. Using a graphing calculator or other graphing device, estimate the x- and y-values of the maximum point for the graph (the first such point where x > 0). It may be helpful to express the x-value as a multiple of π.
3. Now consider other graphs of the form y = A sin x + B cos x for various values of A and B. Sketch the graph when A = 2 and B = 1, and, find the x - and y-values for the maximum point. (Remember to express the x-value as a multiple of π, if possible.) Has it moved?
4. Repeat and sketch the graph for A = 1, B = 2. Is there any relationship to what you found in part (2)?
5. Explain what you have discovered from completing this activity using details and examples.

Solution

Question 1

The $sin$ and $cos$ functions are periodic, as we know that it represents the state of trigonometric circle. The period of the function is $2\pi$, that is, ${360}^{\circ }$.

After $2\pi$, the function repeats itself from 0 ($2\pi$) till $4\pi$ (${720}^{\circ }$) where a full cycle is completed, and a new cycle starts till infinity.

Question 2

• The graph below shows the periodic nature of the function $sin(x)+cos(x)$ where the max point is $(\frac{3\pi }{4},sin(\frac{\pi }{4})+cos(\frac{\pi }{4}))$ and the min point is $(\frac{7\pi }{4},sin(\frac{-3\pi }{4})+cos(\frac{-3\pi }{4}))$ in the first cycle.

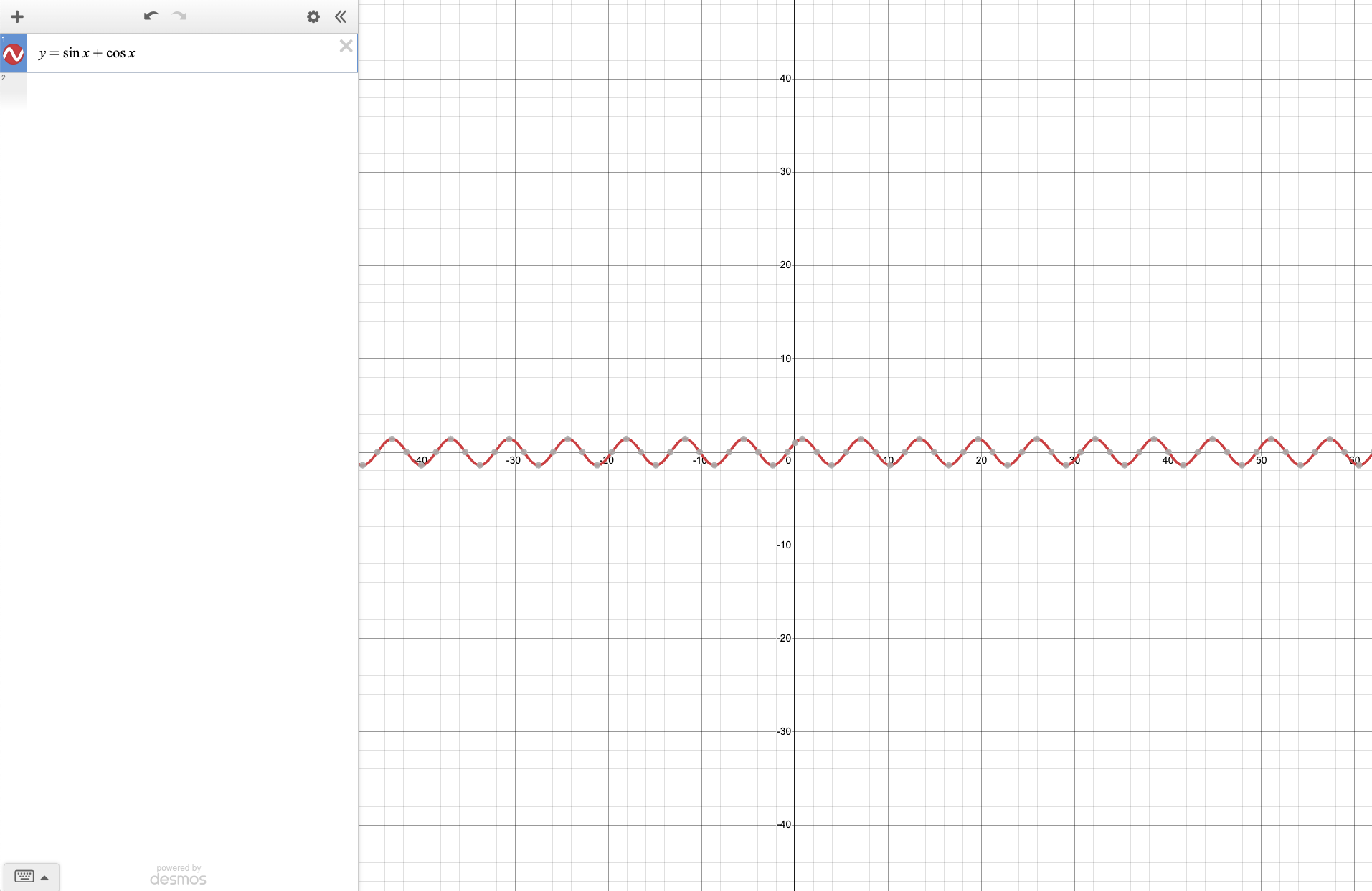
Question 3 And 4

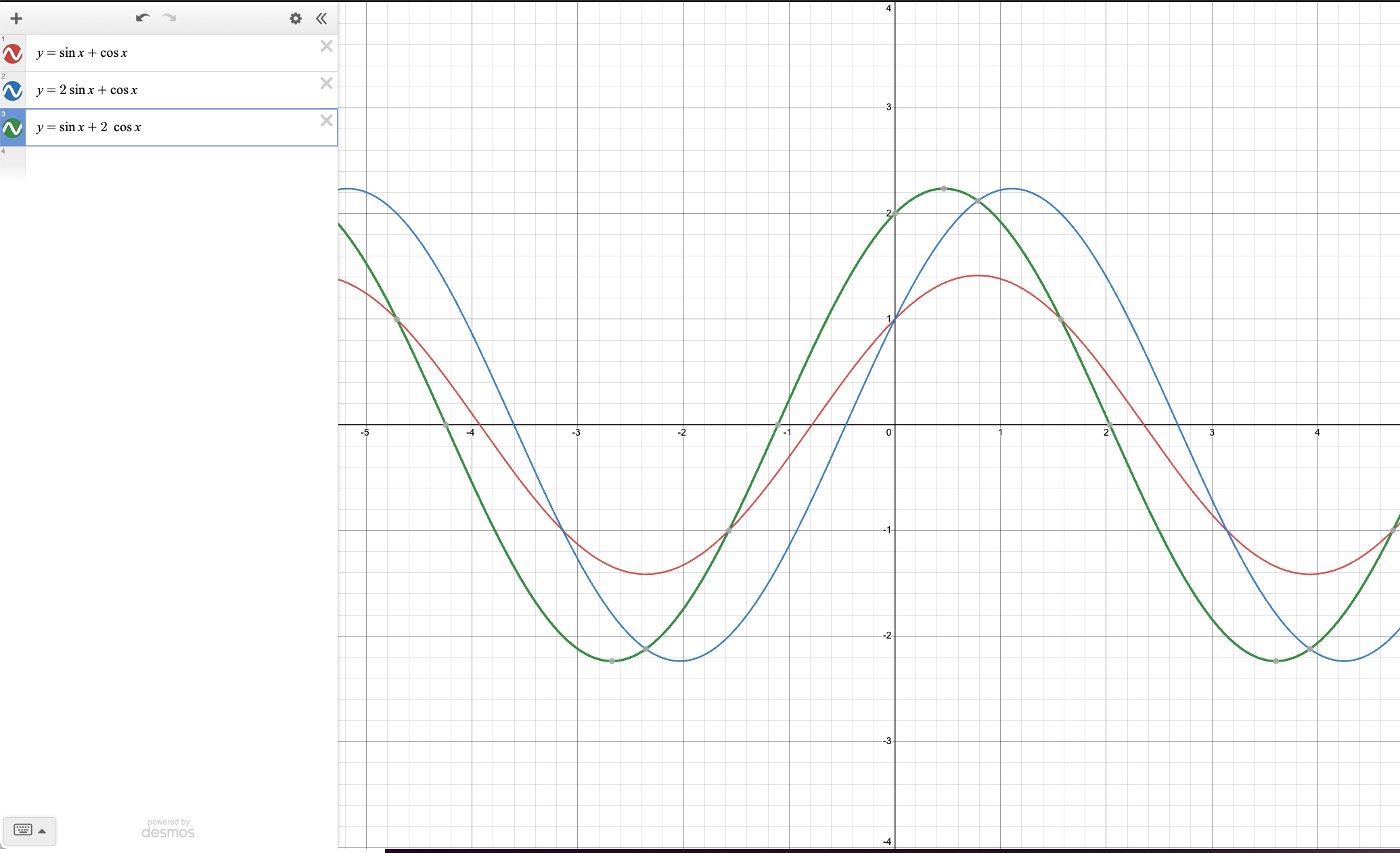
The graph below shows three functions,

• $sin(x)+cos(x)$ represented by the red line.
• $2sin(x)+cos(x)$ represented by the blue line.
• $sin(x)+2cos(x)$ represented by the green line.

We notice the following:

• Max and min points are shifted vertically by the factor of $A$ and $B$ (their values are amplified by the factor of both $A$ and $B$).
• The $x$ value of the max and min points are also shifted accordingly, if we increase A (sin), the $x$ of both min and max will shift right, if we increase B (cos), the $x$ of both min and max will shift left.

Question 5

The standard periodic function of $Asin(x)+Bcos(x)$ where $A$ and $B$ are constants equals 1. Any change in the value of $A$ and $B$ will change the amplitude of the function, and the max and min points will be shifted vertically by the factor of $A$ and $B$. Also the $x$ value of the max and min points are also shifted accordingly (left or right).