DA1. Operations on Sets¶
Statement¶
- Create three sets A, B having 4 elements in each, and U, a Universal set of any possible number of elements of your interest.
- Then explain the answers to the following questions to your peers:
- \(A ∪ B\)
- \(A ∩ B\)
- \((A ∩ B) ∪ U\)
- The power set of A.
- \(A'\).
- \(∅ ∩ B\).
- \(A × B\).
- \(A - B\).
- \((A - B) ∪ (B - A)\).
- Prove any one De Morgan identity for A and B.
Solution¶
We will use the following sets:
- \(A = \{1, 2, 3, 4\}\)
- \(B = \{3, 5, 6\}\)
- \(U = \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}\)
Answer 1¶
- \(A ∪ B = \{1, 2, 3, 4, 5, 6\}\)
- Reads as “A union B”, which is the set of all elements that are in A or B or both (either A or B).
Answer 2¶
- \(A ∩ B = \{3\}\)
- Reads as “A intersect B”, which is the set of all elements that are in both A and B (both A and B).
Answer 3¶
\[
\begin{aligned}
(A ∩ B) ∪ U &= \{3\} ∪ U \\
&= U \\
&= \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}
\end{aligned}
\]
- Reads as “(A intersect B) union U”, which is the set of all elements that are in both A and B or in U.
Answer 4¶
\[
\begin{aligned}
\mathcal{p}(A) = \{ \\
&\,\, \emptyset, \\
&\,\, \{1\}, \{2\}, \{3\}, \{4\}, \\
&\,\, \{1, 2\}, \{1, 3\}, \{1, 4\}, \{2, 3\}, \{2, 4\}, \{3, 4\}, \\
&\,\, \{1, 2, 3\}, \{1, 2, 4\}, \{1, 3, 4\}, \{2, 3, 4\}, \\
&\,\, \{1, 2, 3, 4\} \\
\}
\end{aligned}
\]
- The power set of A is the set of all possible subsets of A.
- The empty set is a subset of every set, so it is included in \(\mathcal{p}(A)\).
- The subsets that have the same elements but are in different order do not count as different subsets, so \(\{1, 2\}\) and \(\{2, 1\}\) are the same subset.
Answer 5¶
- \(A' = \{5, 6, 7, 8, 9, 10\}\)
- Reads as “the complement of A”, and can be represented as \(\bar{A}\) or \(A^c\), and includes all elements that are not in A, but do exist in the universal set U.
- In other words, \(A' = U - A = \{5, 6, 7, 8, 9, 10\}\).
Answer 6¶
- \(∅ ∩ B = ∅\)
- Reads as “the empty set intersect B”, which is the set of all elements that are in both the empty set and B.
- This statement always returns the empty set, no matter what B is.
Answer 7¶
\[
\begin{aligned}
A × B &= \{ \\
&\,\, (1, 3), (1, 5), (1, 6), \\
&\,\, (2, 3), (2, 5), (2, 6), \\
&\,\, (3, 3), (3, 5), (3, 6), \\
&\,\, (4, 3), (4, 5), (4, 6) \\
\}
\end{aligned}
\]
- Reads as “A times B” which results in the cartesian product of A and B, which in turn means all possible ordered pairs of elements from A and B.
Answer 8¶
- \(A - B = \{1, 2, 4\}\)
- Reads as “A minus B”, which is the set of all elements that are in A but not in B.
Answer 9¶
\[
\begin{aligned}
(A - B) ∪ (B - A) &= \{1, 2, 4\} ∪ \{5, 6\} \\
&= \{1, 2, 4, 5, 6\}
\end{aligned}
\]
- Reads as “(A minus B) union (B minus A)”, which is the set of all elements that are in A but not in B or in B but not in A.
Answer 10¶
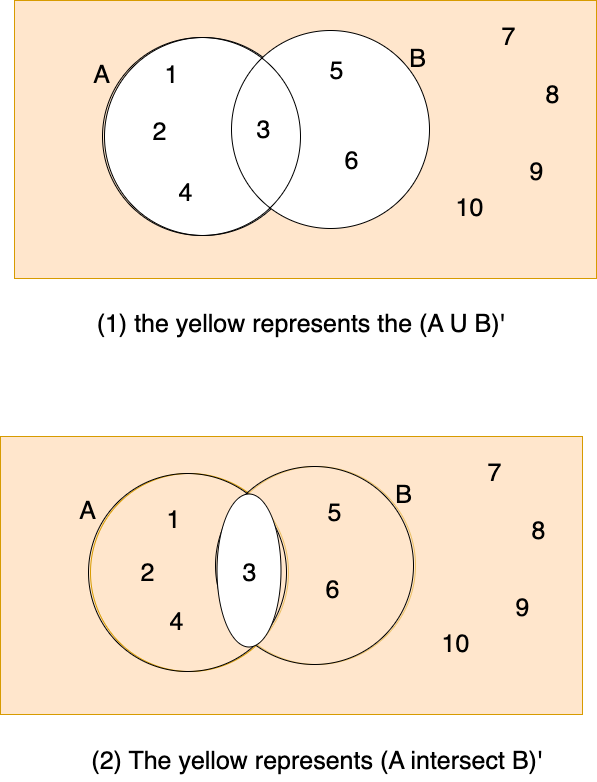
- De Morgan’s Law Includes two dualities:
- \((A ∪ B)' = A' ∩ B'\)
- \((A ∩ B)' = A' ∪ B'\)
- I will use the Venn diagram below to prove the identity.
- (1). We can compare the colored area representing \((A ∪ B)'\) with the colored area representing \(A' ∩ B'\), and find that they are the same.
- (2). We can also compare the colored area representing \((A ∩ B)'\) with the colored area representing \(A' ∪ B'\), and find that they are the same.
References¶
- Doerr, A., & Levasseur, K. (2022). Applied discrete structures (3rd ed.). licensed under CC BY-NC-SA. Chapter 4: More on Sets.
- Levin, O. (2021). Discrete mathematics: An open introduction (3rd ed.). licensed under CC 4.0. Chapter 0: Introduction.