WA7. Newton’s Method, Antiderivative, and L’Hopital’s Rule Exercises
Question 1
1. Calculate the indicated limit. \(\displaystyle \lim_{x \to 3} \frac{x^2+4x-21}{x^2-7x+12}\) . If a limit does not exist then answer \(+ \infty , – \infty\) , or DNE (whichever is correct). Make sure to check that L’Hopital’s rule applies before using it. Also, whenever you apply L’Hopitals rule, indicate that you are using it .
let’s find the limit as x approaches 3:
\[
\begin{aligned}
\lim_{x \to 3} \frac{x^2+4x-21}{x^2-7x+12} &= \frac{3^2 + 12 - 21}{3^2 - 21 + 12} \\
&= \frac{9 + 12 - 21}{9 - 21 + 12} \\
&= \frac{0}{0} \\
\end{aligned}
\]
So the limit is 0/0, which is indeterminate . We can use L’Hopital’s rule to find the limit in such cases. Let’s find the derivative of the numerator and denominator and find the limit of derivatives:
\[
\begin{aligned}
\lim_{x \to 3} \frac{x^2+4x-21}{x^2-7x+12} &= \lim_{x \to 3}\frac{(x^2+4x-21)'}{(x^2-7x+12)'} \\
&= \lim_{x \to 3} \frac{2x+4}{2x-7} \\
&= \frac{2(3)+4}{2(3)-7} \\
&= \frac{10}{-1} \\
&= -10
\end{aligned}
\]
According to L’Hopital’s rule, the limit of the original function is equal to the limit of the derivative of the numerator divided by the derivative of the denominator. So the limit of the original function is -10 .
Question 2
2. Calculate the indicated limit. \(\displaystyle \lim_{x \to 0} \frac{tan3x}{ln(1+x)}\) . If a limit does not exist then answer \(+ \infty , – \infty , or DNE\) (whichever is correct). Make sure to check that L’Hopital’s rule applies before using it. Also, whenever you apply L’Hopitals rule, indicate that you are using it .
let’s find the limit as x approaches 0:
\[
\begin{aligned}
\lim_{x \to 0} \frac{tan3x}{ln(1+x)} &= \frac{tan(3(0))}{ln(1+0)} \\
&= \frac{tan(0)}{ln(1)} \\
&= \frac{0}{0} \\
\end{aligned}
\]
So the limit is 0/0, which is indeterminate . We can use L’Hopital’s rule:
\[
\begin{aligned}
\lim_{x \to 0} \frac{tan3x}{ln(1+x)} &= \lim_{x \to 0}\frac{(tan3x)'}{(ln(1+x))'} \\
&= \lim_{x \to 0} \frac{3sec^2(3x)}{\frac{1}{1+x}} \\
&= \frac{3sec^2(3(0))}{\frac{1}{1+0}} \\
&= \frac{3sec^2(0)}{\frac{1}{1}} \\
&= \frac{3(1)}{1} \\
&= 3
\end{aligned}
\]
So the limit of the original function is 3 .
Question 3
3. Calculate the indicated limit. \(\displaystyle \lim_{x \to 0} \frac{sinx-x}{x^2}\) . If a limit does not exist then answer \(+ \infty , – \infty , or DNE\) (whichever is correct). Make sure to check that L’Hopital’s rule applies before using it. Also, whenever you apply L’Hopitals rule, indicate that you are using it .
let’s find the limit as x approaches 0:
\[
\begin{aligned}
\lim_{x \to 0} \frac{sinx-x}{x^2} &= \frac{sin(0)-0}{0^2} \\
&= \frac{0}{0} \\
\end{aligned}
\]
So the limit is 0/0, which is indeterminate . We can use L’Hopital’s rule:
\[
\begin{aligned}
\lim_{x \to 0} \frac{sinx-x}{x^2} &= \lim_{x \to 0}\frac{(sinx-x)'}{(x^2)'} \\
&= \lim_{x \to 0} \frac{cosx-1}{2x} \\
&= \frac{cos(0)-1}{2(0)} \\
&= \frac{1-1}{0} \\
&= \frac{0}{0} \\
\end{aligned}
\]
We see that the limit is still indeterminate. According to (Dawkins, 2022), we can use L’Hopital’s rule again on the derivative of the original function, that is \(\frac{cosx-1}{2x}\) :
\[
\begin{aligned}
\lim_{x \to 0} \frac{cosx-1}{2x} &= \lim_{x \to 0}\frac{(cosx-1)'}{(2x)'} \\
&= \lim_{x \to 0} \frac{-sinx}{2} \\
&= \frac{-sin(0)}{2} \\
&= \frac{0}{2} \\
&= 0 \\
\end{aligned}
\]
So the limit of the original function is 0 .
Question 4
4. Calculate the indicated limit. \(\displaystyle \lim_{x \to } \frac{sin(6x)}{sin(3x)}\) . If a limit does not exist then answer \(+ \infty , – \infty , or DNE\) (whichever is correct). Make sure to check that L’Hopital’s rule applies before using it. Also, whenever you apply L’Hopitals rule, indicate that you are using it .
let’s find the limit as x approaches 0:
\[
\begin{aligned}
\lim_{x \to 0} \frac{sin(6x)}{sin(3x)} &= \frac{sin(6(0))}{sin(3(0))} \\
&= \frac{sin(0)}{sin(0)} \\
&= \frac{0}{0} \\
\end{aligned}
\]
So the limit is 0/0, which is indeterminate . We can use L’Hopital’s rule:
\[
\begin{aligned}
\lim_{x \to 0} \frac{sin(6x)}{sin(3x)} &= \lim_{x \to 0}\frac{(sin(6x))'}{(sin(3x))'} \\
&= \lim_{x \to 0} \frac{6cos(6x)}{3cos(3x)} \\
&= \frac{6cos(6(0))}{3cos(3(0))} \\
&= \frac{6cos(0)}{3cos(0)} \\
&= \frac{6(1)}{3(1)} \\
&= \frac{6}{3} \\
&= 2 \\
\end{aligned}
\]
So the limit of the original function is 2 .
Question 5
5. Which of the following are indeterminate forms? \(\frac{0}{0} , \frac{0}{ \infty } , \frac{ \infty }{0} , \frac{ \infty}{\infty}\) .
Indeterminate forms are forms that cannot be evaluated to a single value directly. They are:
\(\frac{0}{0}\) \(\frac{ \infty}{\infty}\)
The following are not indeterminate forms:
\(\frac{0}{ \infty }\) as it is evaluates to 0\(\frac{ \infty }{0}\) as it evaluates to \(\infty\)
Question 6
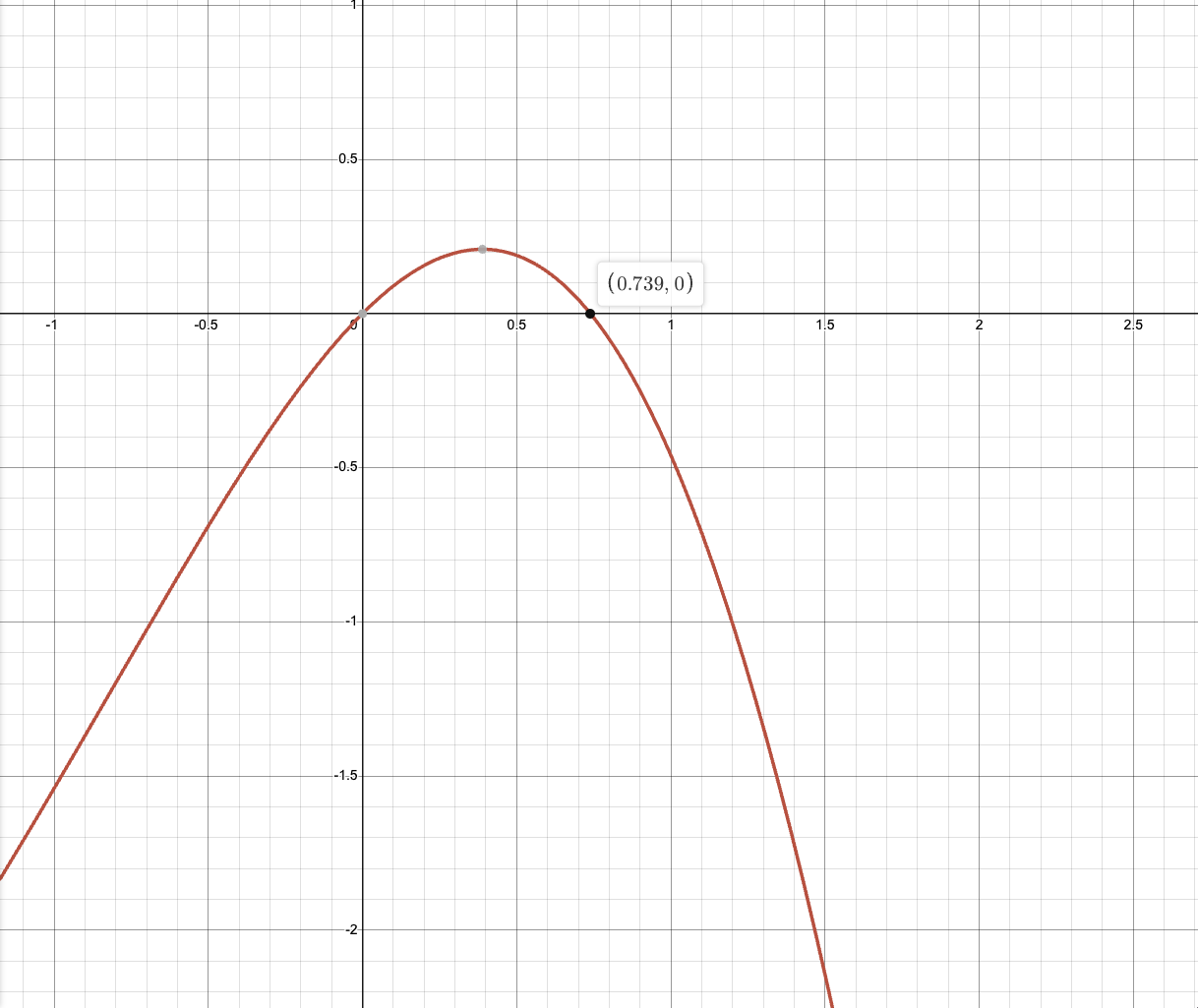
6. Use Newton’s Method to determine \(x_1\) and \(x_2\) for the function \(f(x)=x cos (x)-x^2\) and the value of \(x_0=1\) .
Newton’s method is used to find the roots of a function. The formula is:
\[
x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}
\]
let’s derive the function \(f(x)=x cos (x)-x^2\) :
\[
\begin{aligned}
f(x) &= x cos (x)-x^2 \\
f'(x) &= cos(x) + x(-sin(x)) - 2x \\
&= cos(x) - xsin(x) - 2x \\
\end{aligned}
\]
First iteration: we will start from \(x_0=1\) :
\[
\begin{aligned}
x_1 &= x_0 - \frac{f(x_0)}{f'(x_0)} \\
&= 1 - \frac{f(1)}{f'(1)} \\
&= 1 - \frac{(1)cos(1)-(1)^2}{cos(1) - (1)sin(1) - 2(1)} \\
&= 1 - \frac{cos(1)-1}{cos(1) - sin(1) - 2} \\
&= 1 - \frac{0.5403-1}{0.5403 - 0.8415 - 2} \\
&= 1 - \frac{-0.4597}{-1.3002} \\
&= 1 - 0.3537 \\
&= 0.6463 \\
\end{aligned}
\]
Second iteration: we will start from \(x_1=0.6463\) :
\[
\begin{aligned}
x_2 &= x_1 - \frac{f(x_1)}{f'(x_1)} \\
&= 0.6463 - \frac{f(0.6463)}{f'(0.6463)} \\
&= 0.6463 - \frac{(0.6463)cos(0.6463)-(0.6463)^2}{cos(0.6463) - (0.6463)sin(0.6463) - 2(0.6463)} \\
&= 0.6463 - \frac{0.6463cos(0.6463)-0.4177}{cos(0.6463) - sin(0.6463) - 1.2926} \\
&= 0.6463 - \frac{0.6463(0.7968)-0.4177}{0.7968 - 0.6031 - 1.2926} \\
&= 0.6463 - \frac{0.5142-0.4177}{0.7968 - 0.6031 - 1.2926} \\
&= 0.6463 - \frac{0.0965}{-1.099} \\
&= 0.6463 + 0.0878 \\
&= 0.7341 \\
\end{aligned}
\]
So \(x_1=0.6463\) and \(x_2=0.7341\) .
Question 7
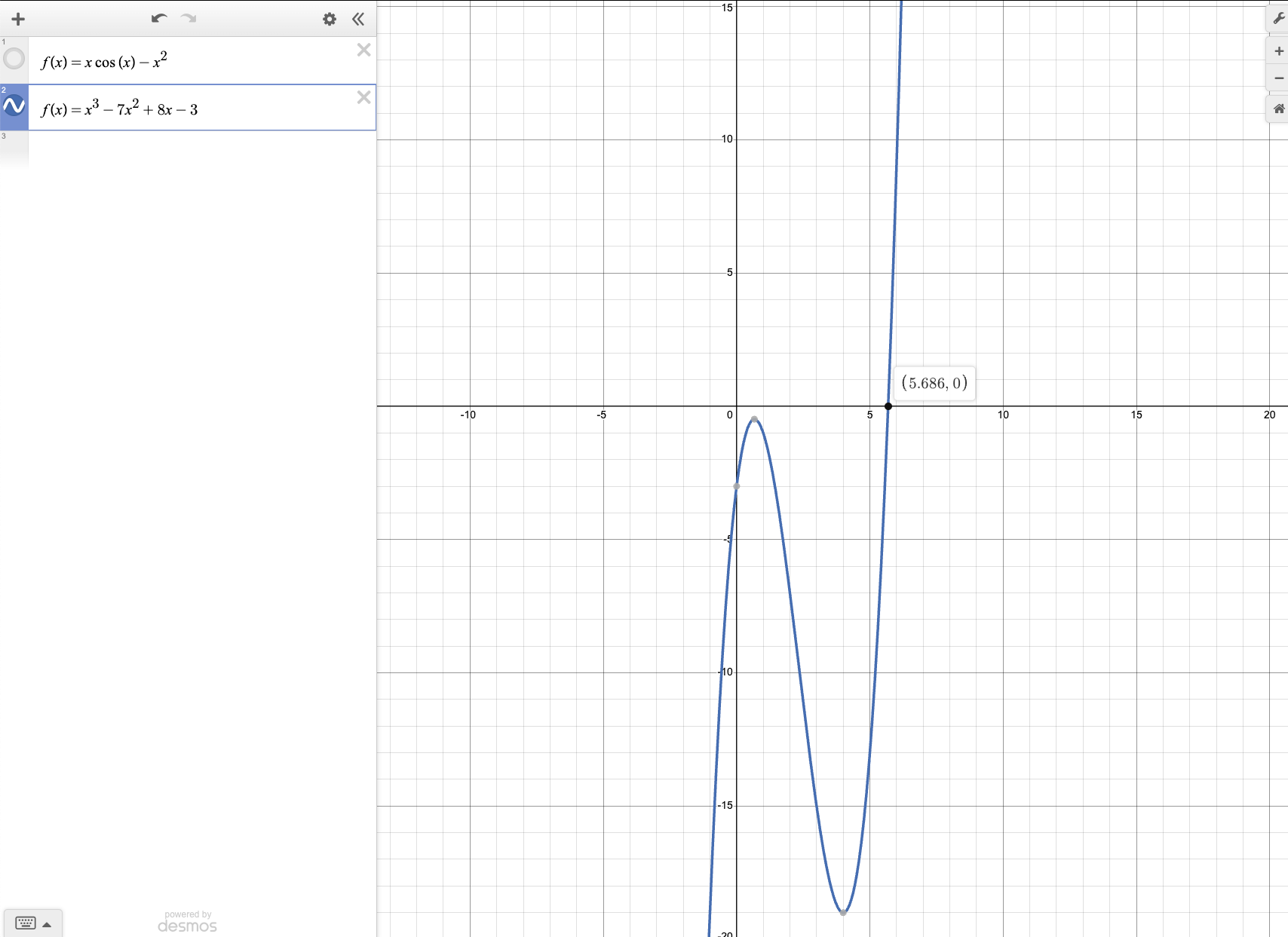
7. Use Newton’s Method to determine \(x_1\) and \(x_2\) for the function \(f(x)=x^3-7x^2+8x-3\) and the value of \(x_0=5\) .
Let’s derive the function \(f(x)=x^3-7x^2+8x-3\) :
\[
\begin{aligned}
f(x) &= x^3-7x^2+8x-3 \\
f'(x) &= 3x^2 - 14x + 8 \\
\end{aligned}
\]
First iteration: we will start from \(x_0=5\) :
\[
\begin{aligned}
x_1 &= x_0 - \frac{f(x_0)}{f'(x_0)} \\
&= 5 - \frac{f(5)}{f'(5)} \\
&= 5 - \frac{(5)^3-7(5)^2+8(5)-3}{3(5)^2 - 14(5) + 8} \\
&= 5 - \frac{125-175+40-3}{75 - 70 + 8} \\
&= 5 - \frac{-13}{13} \\
&= 5 + 1 \\
&= 6 \\
\end{aligned}
\]
Second iteration: we will start from \(x_1=6\) :
\[
\begin{aligned}
x_2 &= x_1 - \frac{f(x_1)}{f'(x_1)} \\
&= 6 - \frac{f(6)}{f'(6)} \\
&= 6 - \frac{(6)^3-7(6)^2+8(6)-3}{3(6)^2 - 14(6) + 8} \\
&= 6 - \frac{216-252+48-3}{108 - 84 + 8} \\
&= 6 - \frac{9}{32} \\
&= 6 - 0.2813 \\
&= 5.7187 \\
\end{aligned}
\]
So \(x_1=6\) and \(x_2=5.7187\) .
Question 8
8. Find the antiderivative of the following functions :
a) \(f(x)=3\) .
\[
\begin{aligned}
\int (3) dx &= 3x + C \\
\end{aligned}
\]
b) \(f(x)=2x\) .
\[
\begin{aligned}
\int (2x) dx &= x^2 + C \\
\end{aligned}
\]
c) \(f(x)=5x^4\) .
\[
\begin{aligned}
\int (5x^4) dx &= \frac{5x^5}{5} + C \\
&= x^5 + C \\
\end{aligned}
\]
Question 9
9. Find the antiderivative of the following functions :
a) \(f(x)=sinx\) .
\[
\begin{aligned}
\int (sinx) dx &= -cosx + C \\
\end{aligned}
\]
b) \(f(x)=sec^2x\) .
\[
\begin{aligned}
\int (sec^2x) dx &= tanx + C \\
\end{aligned}
\]
c) \(f(x)= \sqrt[3]{x}\) .
\[
\begin{aligned}
\int ( \sqrt[3]{x}) dx &= \frac{x^{\frac{1}{3}+1}}{\frac{1}{3}+1} + C \\
&= \frac{x^{\frac{4}{3}}}{\frac{4}{3}} + C \\
&= \frac{3}{4} x^{\frac{4}{3}} + C \\
&= \frac{3}{4} \sqrt[3]{x^4} + C \\
\end{aligned}
\]
Question 10
10. Find the antiderivative of the following functions :
a) \(f(x)=12-x\) .
\[
\begin{aligned}
\int (12-x) dx &= 12x - \frac{x^2}{2} + C \\
\end{aligned}
\]
b) \(f(x)=8x^3-9x^2+4\) .
\[
\begin{aligned}
\int (8x^3-9x^2+4) dx &= 8 \frac{x^4}{4} - 9 \frac{x^3}{3} + 4x + C \\
&= 2x^4 - 3x^3 + 4x + C \\
\end{aligned}
\]
c) \(f(x)= \frac{1}{(3x)^2}\) .
\[
\begin{aligned}
\int ( \frac{1}{(3x)^2}) dx &= \frac{1}{3^2} \int ( \frac{1}{x^2}) dx \\
&= \frac{1}{9} \int (x^{-2}) dx \\
&= \frac{1}{9} \frac{x^{-2+1}}{-2+1} + C \\
&= \frac{1}{9} \frac{x^{-1}}{-1} + C \\
&= -\frac{1}{9} \frac{1}{x} + C \\
&= -\frac{1}{9x} + C \\
\end{aligned}
\]
References
November 12, 2023
November 12, 2023