Skip to content

JA2. Learning Journal 2

Statement

There are two parts A and B to this assignment, and you must submit both parts with steps and proper explanations. Answer the following questions based on the knowledge gained by you on the different applications of divide and conquer algorithm.

Part A:

  • Sort the following list using the optimal divide-and-conquer algorithm: 36, 25, 44, 2, 8, 88, 11.
  • Which application of the divide and conquer algorithm you will use for this purpose? Explain it.
  • List and explain all the intermediary steps of the algorithm to sort the above list.
  • Explain the space and time complexities of the algorithm used by you for sorting the list.
  • Note: Optimal algorithms often use minimal memory or have low space complexity, especially in situations where memory resources are limited.
  • Include the following items in your explanation:
    • Propose the most appropriate algorithm.
    • Submit a step-by-step solution and explain in your own words.
    • Share the sorted list at the end.
    • Discuss the space and time complexities of the algorithm.

Part B:

  • You are an employee of a warehouse and have been provided with 7 identical cartons and a measuring instrument.
  • 6 of the 7 cartons are equal in weight and 1 of the 7 given cartons has less material and thus weighs less.
  • Your task is to find the less weighing carton in exactly two measurements.
  • Submit a step-by-step solution for the above problem applying the technique of divide-and-conquer.
  • Hints:
    • The input is not a sorted.
    • Consider that the cartons are labelled as C1, C2, C3, C4, C5, C6, C7.
    • You may start by dividing the 7 Cartons into three groups.

Answer

Introduction

Divide and conquer is a strategy for solving problems that involves dividing the problem into smaller sub-problems, solving the sub-problems recursively, and then combining the sub-solutions to create a solution to the main problem. Each of this steps affects the running time of a divide-and-conquer algorithm, and the combining step is particularly important, as an expensive combine may negate the benefits of the divide-and-conquer strategy (Leiserson, 2005).

This text will use the merge sort algorithm to sort the list in part A of the prompt. For part B, the text will use a divide-and-conquer strategy that divides the problem into 3 groups of size 3.

Part A: Sorting the list

MergeSort is a divide and conquer algorithm that divides the input list into two halves, recursively sorts the two halves, and then merges the sorted halves. The algorithm has a time complexity of T(n) = 2T(n/2) + O(n) or O(n log n) and a space complexity of O(n) (Leiserson, 2005) with a simple pseudocode as follows:

def mergeSort(arr):
    if (n >1):
        return merge(mergeSort(arr[:n//2]), mergeSort(arr[n//2:]))
    else:
        return arr

Notice how the merge routine plays a significant role in the algorithm. It simply compares the first element of the two merged lists (guaranteed to be sorted), and inserts the smaller element into the new list.

Below is a graph that represent all the intermediary steps of the algorithm to sort the list 36, 25, 44, 2, 8, 88, 11, done using the mermaid library:

Image 1: MergeSort Graph showing intermediate steps
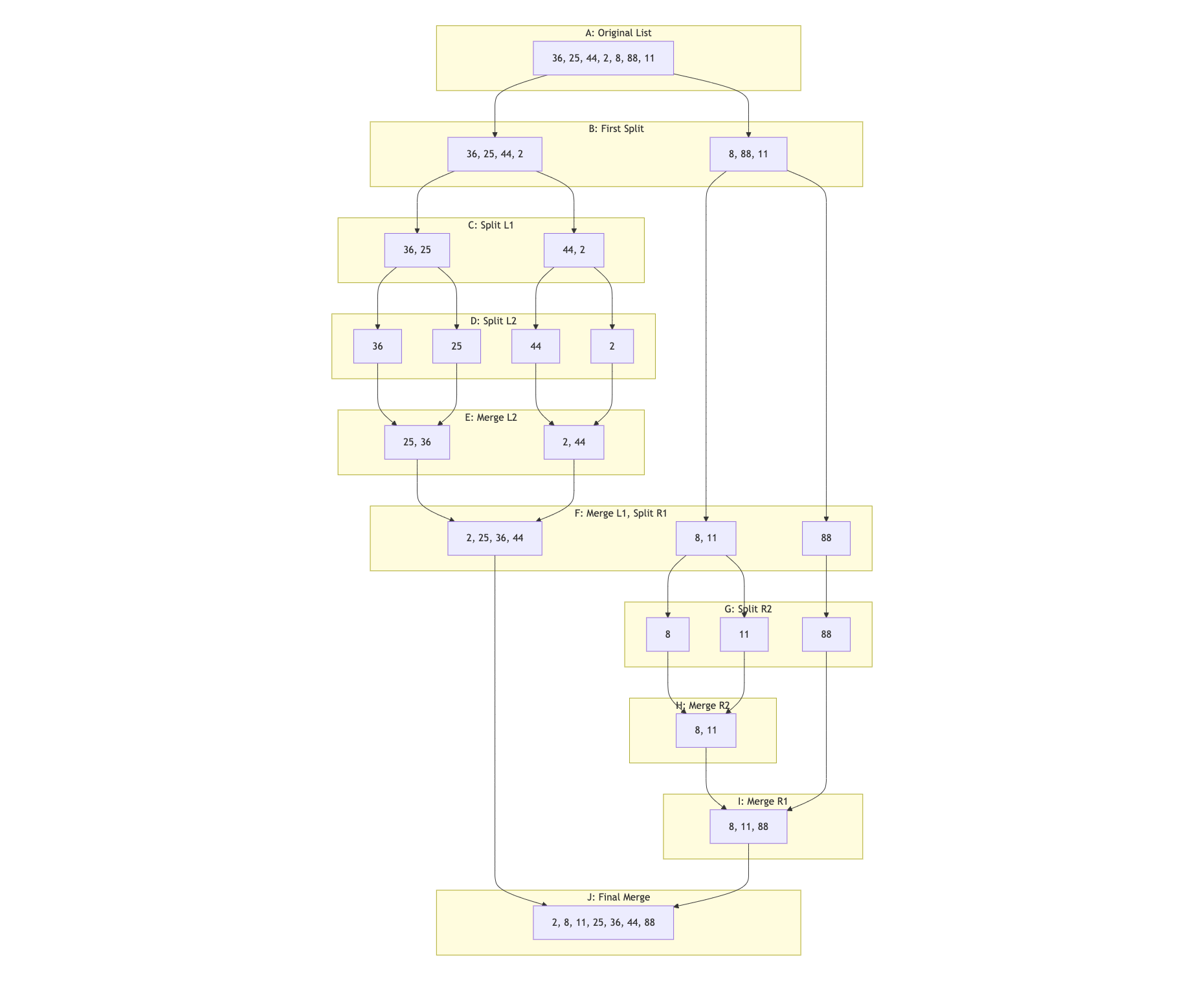MergeSort Graph

The sorted list is [2, 8, 11, 25, 36, 44, 88], and the steps in the graph above are divided into levels (yellow boxes) labeled with letters A to J, and here is a brief explanation of each level:

  • A: Original List: the original list [36, 25, 44, 2, 8, 88, 11] is inputted.
  • B: First Split: the list is split into two halves [36, 25, 44, 2] and [8, 88, 11].
  • The processor process each half separately, finishing the left half first (split, sort, merge) in steps B to F, and then going to the right half in steps F to J.
  • C: Split L1: the left half is split into [36, 25] and [44, 2].
  • D: Split L2: the left half is split into single elements [36], [25], [44], and [2].
  • E: Merge L2: the single elements are merged into [25, 36] and [2, 44]; notice how each of the newly formed lists is sorted.
  • F: Merge L1, Split R1: the left half is merged into [2, 25, 36, 44], and the right half is split into [8, 11] and [88] (connected to step B).
  • G: Split R2: the right half is split into single elements [8], [11], and [88].
  • H: Merge R2: the single elements are merged into [8, 11].
  • I: Merge R1: the right half is merged into [8, 11, 88].
  • J: Final Merge: the two sorted halves are now merged into the final sorted list [2, 8, 11, 25, 36, 44, 88].

To discuss the time and space complexities of the MergeSort for an array of size n; we would assume that swapping elements in the array happens in-place; that is there is no need for additional memory to store copies of the results in intermediate steps; hence, the array does not need extra space except for its original array of O(n).

The time complexity of the algorithm is O(n log n) following the master theorem for T(n) = 2T(n/2) + O(n); where a = 2, b = 2, and f(n) = O(n), and log_b(a) = log_2(2) = 1. The time complexity is O(n^d \log n) = O(n log n) (Vazirani et al., n.d.).

Part B: Finding the less weighing carton

This problem is similar to Santa’s dirty socks problem mentioned in the reading. It can be solved using divide and conquer according to this strategy:

  • Divide 1: divide the cartons into three groups of 3, C1, C2, C3, C4, C5, C6, and C7 (there is only one carton in this group).
  • Measurement 1: weigh the first two groups, C1, C2, C3 and C4, C5, C6.
  • If these groups are equal, then the box that is left alone is the lighter box C7.
  • If the groups are not equal, then we need to focus on the lighter group as it contains the lighter carton; let’s assume that it is C1, C2, C3.
  • Divide 2: divide this group into three groups of 1, C1, C2, and C3.
  • Measurement 2: weigh C1 and C2.
  • If these two are equal, then C3 is the lighter carton.
  • If they are not equal, then the lighter carton is the one that is the one we are interested in.

Below is a graph that represents the steps in the algorithm to find the less weighing carton, done using the mermaid library:

Image 2: Weighing Cartons Graph
Weighing Cartons Graph

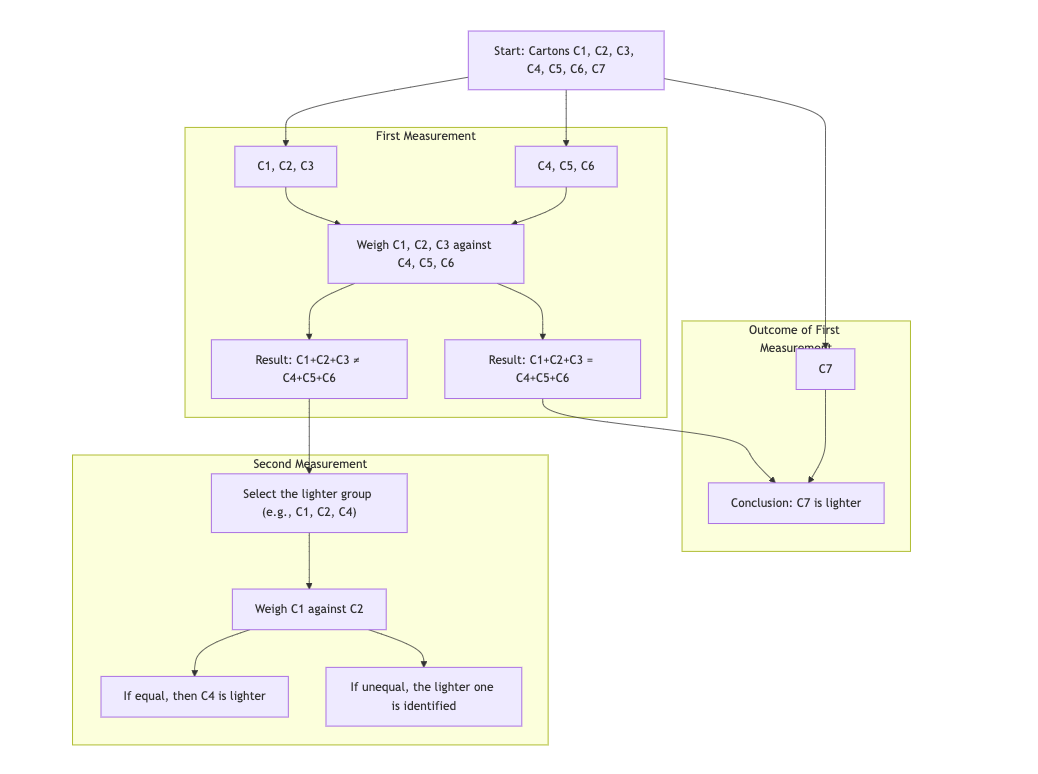Conclusion

To conclude, divide and conquer is a powerful strategy for solving problems that involves 3 steps: divide, solve recursively, and combine. In the sorting problem of part A, we keep simplifying the problem until it reaches 1 comparison between two elements (in the merge step), or no comparison at all (in the base case). In the weighing cartons problem of part B, we keep discarding heavier boxes in bulk as we divide the problem eliminating the need of one to one comparison for each box.

References