DA3. DFS and BFS¶
Statement¶
In this unit, you have learned about Depth-first search (DFS), Breadth-first search (BFS) Consider the following directed graph and perform DFS and BFS where S is the starting node and G is the goal node.
- For both search strategies, you must show the search tree diagram and the final path to reach the goal node (G).
- Then, describe in your own words, which search strategy is a better choice for this given graph problem. Your comparison should mention about time and space/memory complexity.
- Finally, in the field of AI, where the optimal solution is highly expected, what are the factors you should consider before choosing the right search algorithm?
Answer¶
Introduction¶
Graph is a data structure that consists of nodes and edges that connect those nodes, and it covers some common data structures like trees. Graphs are useful to represent many real-world problems, such as social networks, maps, and networks. Graph traversal is the process of visiting all the nodes in a graph in a specific order (Poole & Mackworth, 2017).
There are two common methods to traverse a graph: depth-first search (DFS) and breadth-first search (BFS), which are both examples of greedy algorithms; but they differ by the way they select the pool of nodes (frontier) to visit next. The text will discuss a path chosen by DFS and BFS separately, compare them using the given graph, and conclude with discussing the search problem within the field of AI.
DFS Method¶
DFS explores a branch (or a single path) as far as possible before backtracking to the adjacent paths. It recursively selecting the left most child of a node until it reaches a leaf. The table below shows the process of using DFS to find the path from S to G.
| Step | Current Node | Frontier | Next Node | Path So Far |
|---|---|---|---|---|
| 1 | S | C, A | C | S |
| 2 | C | D, B, A | D | S -> C |
| 3 | D | F | F | S -> C -> D |
| 4 | F | G | G | S -> C -> D -> F |
| 5 | G | S -> C -> D -> F -> G |
BFS Method¶
BFS explores all the nodes at the current depth (level) before moving to the next depth. It selects all nodes connected to the current node before moving to the next node. The table below shows the process of using BFS to find the path from S to G.
| Step | Current Node | Frontier | Next Node | Path So Far |
|---|---|---|---|---|
| 1 | S | C, A | C | S |
| 2 | C | D, B, A | B | S -> C |
| 3 | B | F, E | E | S -> C -> B |
| 4 | E | G | G | S -> C -> B -> E |
| 5 | G | S -> C -> B -> E -> G |
Comparison¶
The image below shows both DFS and BFS search trees for the given graph, the red arrows indicate the path to reach the goal node (G).
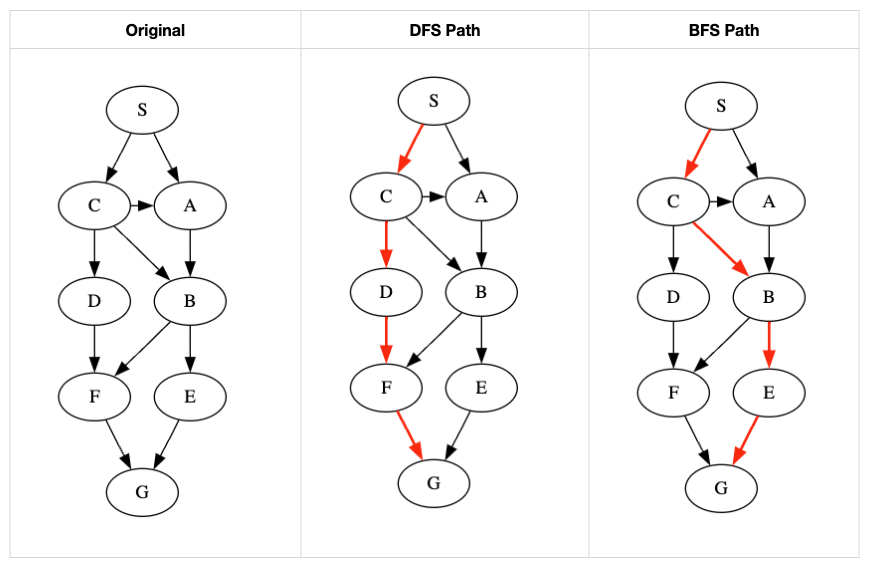
It is important to note that the graph in the prompt is simple and can be traversed using different paths with no ability to show snd advantage of a method over the other, especially as no heuristic is used and all the edges have the same weight or weight.
However, in general, DFS is more memory-efficient than BFS because it uses a stack to store the nodes, while BFS uses a queue. On the other hand, BFS is more time-efficient than DFS because it explores all the nodes at the current depth before moving to the next depth, which makes it more likely to find the shortest path in a graph with weighted edges (Shaffer, 2011).
In general, BFS is complete as it it guaranteed to find a solution if one exists, while DFS is not complete as it may get stuck in an infinite loop if the graph has cycles. A* search is a combination of both methods, where it explores the current level using BFS, and then it selects one path to deeply explore using DFS; and I think it is the best choice for the given graph. The table below summarizes the comparison between DFS, BFS, and A* search (Poole & Mackworth, 2017):
| Strategy | Frontier Selection | Complete | Exit Cycles | Space |
|---|---|---|---|---|
| Depth First | Stack (LIFO) | No | No | Linear |
| Breadth First | Queue (FIFO) | Yes | No | Exponential |
| A* Search | Global Total Min f(p) |
Yes | No | Exponential |
Choosing the Right Search Algorithm¶
Most AI problems can be modeled into a search problem on a graph where the nodes represent the states and the edges represent the actions available to the agent at that state. The choice of the search algorithm depends on the problem’s constraints and requirements, with optimizations such as using heuristics to guide the search, bidirectional search, and parallel search upon splitting the search space into multiple subspaces (islands).
Usually, such problems defines the goal state and leaves finding the path up to the agent; hence, using all available information including prior knowledge to build an informed search strategy is crucial. The choice of the search algorithm is unique to each problem, and the agent should consider the problem’s constraints, the available resources, and the expected solution quality.
References¶
- Poole, D. L., & Mackworth, A. K. (2017). Artificial Intelligence: Foundations of computational agents. Cambridge University Press. https://artint.info/2e/html/ArtInt2e.html
- Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf.