DA7. Bézier Splines¶
Statement¶
Conduct research on the internet and find examples of programs that have implemented Bézier splines, analyze their technique, and report it as part of your discussion assignment. In the Discussion Forum, discuss how a Bézier spline could implement in 3D space using WebGL and the Three.js API.
Answer¶
Introduction¶
Drawing curves on computer is a complex task as the computer requires a function that covers every point on the curve and tell it what to do. Bézier curves are a way to draw curves on computer. They’re named after Pierre Bézier, a French engineer who used them to design car bodies in the 1960s. A spline is a special type of curve that may use interpolation or approximation along with specific type of polynomial functions to define the curve (House, 2014). In this text, we may use the world spline and curve interchangeably.
Bézier Curves (splines)¶
Bézier curves are defined by a set of control points. They are useful for creating smooth curves in procedural geometry. The curve is usually passes through the first and last control points, but not through the intermediate control points. Instead, intermediate points influence the shape of the curve, and the actual points that make up the curve are calculated using a mathematical formula (Massachusetts Institute of Technology, 2020). Cubic Bézier curves are the most common Bézier curves (Holmer, 2021).
In 3D space, Bézier curves uses parametric functions to define the curve, which in turn are a combination of Bernstein polynomials. In other words, the curve is cubic polynomial in nature (Kamermans, 2024). It has at least four control points (P1, P2, P3, P4), and the curve is tangent at P1 to (P1-P2) and at P4 to (P4-P3). The image below shows a cubic Bézier curve (Massachusetts Institute of Technology, 2020):
| Image 1: Cubic Bézier Curve |
|---|
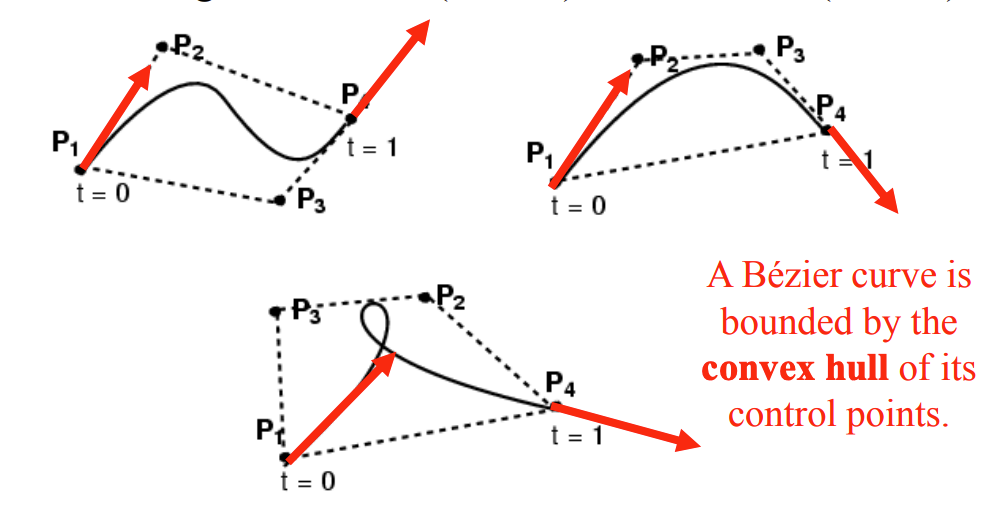 |
Bézier Curves in 3D (WebGL)¶
Bezier spline curves (2001) from Ibiblio.org. provides a good abstraction for Bezier class in JavaScript. Which can be simply called as:
new Bezier(
"c4", // id for 1st canvas
"c42", // id for 2nd canvas
0.4, // scale
[0.5, 0.1, 0.9, 0.9], // control points (X)
[0.1, 0.9, 0.9, 0.1] // control points (Y)
);
In the above example 4 control points are used (0.5, 0.1), (0.1, 0.9), (0.9, 0.
9), (0.9, 0.1) to draw a Bézier curve. The result is shown in the image 2 below:
| Image 2: Bézier Curve in 3D (WebGL) |
|---|
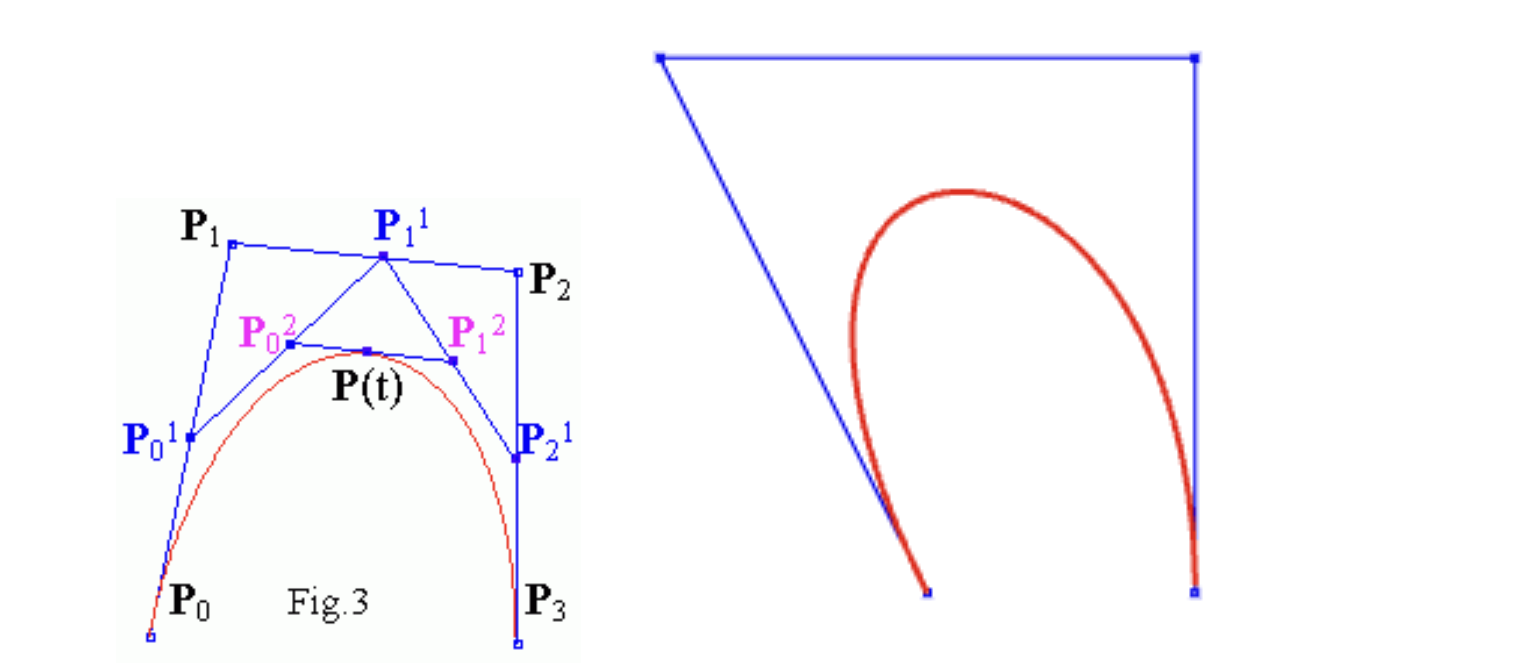 |
The Bezier class uses the drawSpline function to draw the curve. The drawSpline function uses the ctx (canvas context) to draw the curve. The full file is attached in the comments.
function drawSpline() {
var step = 1 / w,
t = step;
var Pxi = new Float64Array(n),
Pyi = new Float64Array(n);
var scPx = new Float64Array(n),
scPy = new Float64Array(n);
var X, Y;
ctx.clearRect(0, 0, w, h);
ctx.lineWidth = d;
ctx.strokeStyle = "#0000f0";
for (var i = 0; i < n; i++) {
X = scPx[i] = Px[i] * w;
Y = scPy[i] = Py[i] * h;
ctx.strokeRect(X - d, h1 - Y - d, d2, d2);
}
if (n > 2) {
ctx.beginPath();
ctx.moveTo(scPx[0], h1 - scPy[0]);
for (var i = 1; i < n; i++) ctx.lineTo(scPx[i], h1 - scPy[i]);
ctx.stroke();
}
ctx.lineWidth = d2;
ctx.strokeStyle = "#f00000";
ctx.beginPath();
ctx.moveTo(scPx[0], h1 - scPy[0]);
for (var k = 1; k < w; k++) {
Pxi.set(scPx);
Pyi.set(scPy);
for (var j = n - 1; j > 0; j--)
for (var i = 0; i < j; i++) {
Pxi[i] = (1 - t) * Pxi[i] + t * Pxi[i + 1];
Pyi[i] = (1 - t) * Pyi[i] + t * Pyi[i + 1];
}
ctx.lineTo(Pxi[0], h1 - Pyi[0]);
t += step;
}
ctx.stroke();
}
Bézier Curves in 3D (Three.js)¶
Using Three.js, we can create a Bézier curve in 3D space with a few lines of code according to Three.js docs (2024):
// prettier-ignore
const curve = new THREE.CubicBezierCurve3(
new THREE.Vector3( -10, 0, 0 ),
new THREE.Vector3( -5, 15, 0 ),
new THREE.Vector3( 20, 15, 0 ),
new THREE.Vector3( 10, 0, 0 )
);
const points = curve.getPoints(50);
const geometry = new THREE.BufferGeometry().setFromPoints(points);
const material = new THREE.LineBasicMaterial({ color: 0xff0000 });
const curveObject = new THREE.Line(geometry, material);
scene.add(splineObject);
The code above uses THREE.CubicBezierCurve3 to create a cubic Bézier curve in 3D space. The curve is defined by four control points, and the getPoints method is used to get 50 points of the interpolated curve which in turn are used to create a line representing the curve. The output is shown in the image 3 below:
| Image 3: Bézier Curve in 3D (Three.js) |
|---|
 |
Conclusion¶
Bézier curves are a powerful tool for creating smooth curves in computer graphics. They are defined by a set of control points and a mathematical formula that calculates the actual points that make up the curve. In 3D space, Bézier curves can be implemented using WebGL and the Three.js API to create smooth curves in procedural geometry.
References¶
- Bezier spline curves. (2001). Ibiblio.org. https://www.ibiblio.org/e-notes/Splines/bezier.html
- Holmer, F. (2021, August 19). The Beauty of Bézier Curves. YouTube. https://www.youtube.com/watch?v=aVwxzDHniEw
- House, H. D. (2014). CH.14 Spline Curves. Texas A&M University. https://people.computing.clemson.edu/~dhouse/courses/405/notes/splines.pdf
- Kamermans, M. P. (2024, June 19). A Primer on Bézier Curves. Github.io. https://pomax.github.io/bezierinfo/
- Massachusetts Institute of Technology (2020). Coordinates and Transformations. MITOpenCourseware. https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-837-computer-graphics-fall-2012/lecture-notes/.
- Three.js docs. (2024). Threejs.org. https://threejs.org/docs/#api/en/extras/curves/CubicBezierCurve3