Skip to content

JA6. Linear Regression in JASP

Statement

It is natural to think there will be a relationship between the number of calories and the amount of carbohydrates (in grams). In this journal, we will conduct a study using the nutrition data for several Starbucks food items. Click here for the dataset (spreadsheet) or Dataset (pdf)

Import the data to JASP, run the command and take a screenshot of your output. Based on that, answer the following questions.

  1. What is the correlation coefficient (Pearson’s r) between the variable’s calories and carb?
  2. Interpret the strength of the relationship between the calories and the amount of carbohydrates (in grams) contained in the food menu at Starbucks.
  3. Using JASP descriptive statistics, find the mean and standard deviation for the variable calories and carb
  4. In a food label at Starbucks, the number of calories is indicated but the amount of carbohydrates (in grams) is missing. Write the equation of the regression line for prediction of the amount of carbohydrates (the response or dependent variables) given the number of calories (explanatory variable or covariate):
    • First calculate the slope ( b_ 1 ).
    • Calculate the intercept ( b_ 0 ).
    • Write the regression equation.
  5. Using JASP linear regression, validate the regression equation found in c.
  6. Calculate R2 of the regression line for predicting the amount of carbohydrates from the number of calories and interpret it in the context of the application.

Answer

Regression Analysis Process Using JASP

Here is a step by step guide to the analysis performed in JASP, following the guide by Research By Design (2020):

  • Load the data into JASP:
    • Use File > Open from the top menu.
    • Select Computer and then Browse.
    • Select the dataset file.
  • Plot the data to check for conditions:
    • Use Regression > Classical > Correlation from the top menu.
    • Load the x variable (predictor, explanatory) first and then the y variable (response).
    • Select Display Pairwise under Additional Options.
    • Under Plots, select Scatterplot; which allows as to check linearity, outliers, and influential points.
    • Under Plots, select Densities for variables to check for normality.
    • You can use the Assumption Checks to check for the assumptions of linear regression.
  • Do the Regression analysis:
    • Use Regression > Classical > Linear Regression from the top menu.
    • Dependent variable is the y variable.
    • Covariate is the x variable.
    • Set the Method to Enter.
    • Under Statistics:
      • Select Regression Coefficient > Confidence intervals.
      • Select Regression Coefficient > Descriptives.
      • Select Residuals > Statistics to check for outliers and influential points (Std. Residuals should be between -3 and 3).
      • Select Residuals > Durbin-Watson to check for independence of observations (Durbin-Watson statistic should be between 1 - 3).
    • Under Plots:
      • Select Residuals plots > Residuals vs Histogram to check for normality.
      • Select Q-Q plot standardized residuals to check for normality.
      • Select Residuals vs predicted to check for homoscedasticity.

Results of the Analysis

We have loaded the data into JASP and performed both the correlation and linear regression analysis. The results are as follows:

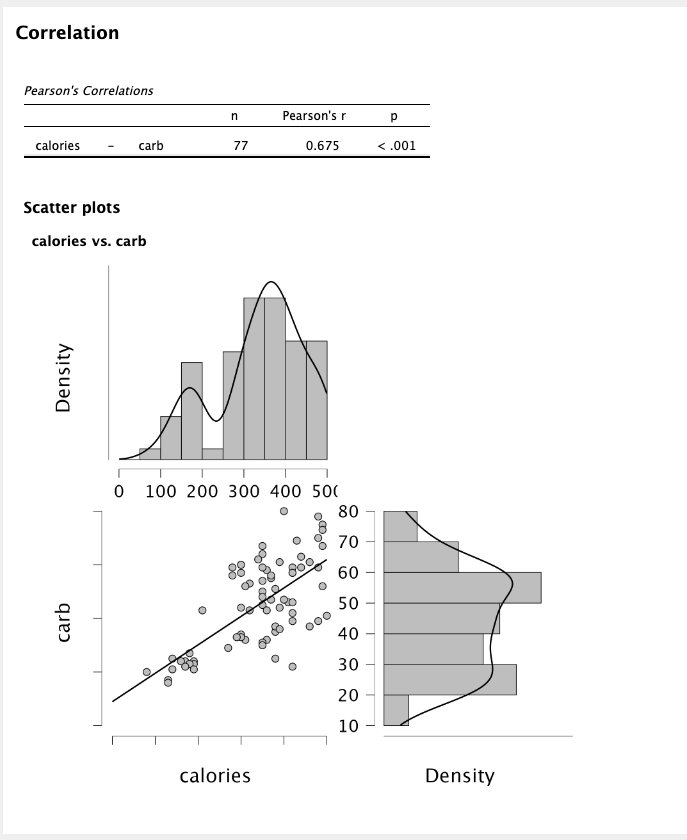Correlation
Figure 1: Correlation between calories and carbs.
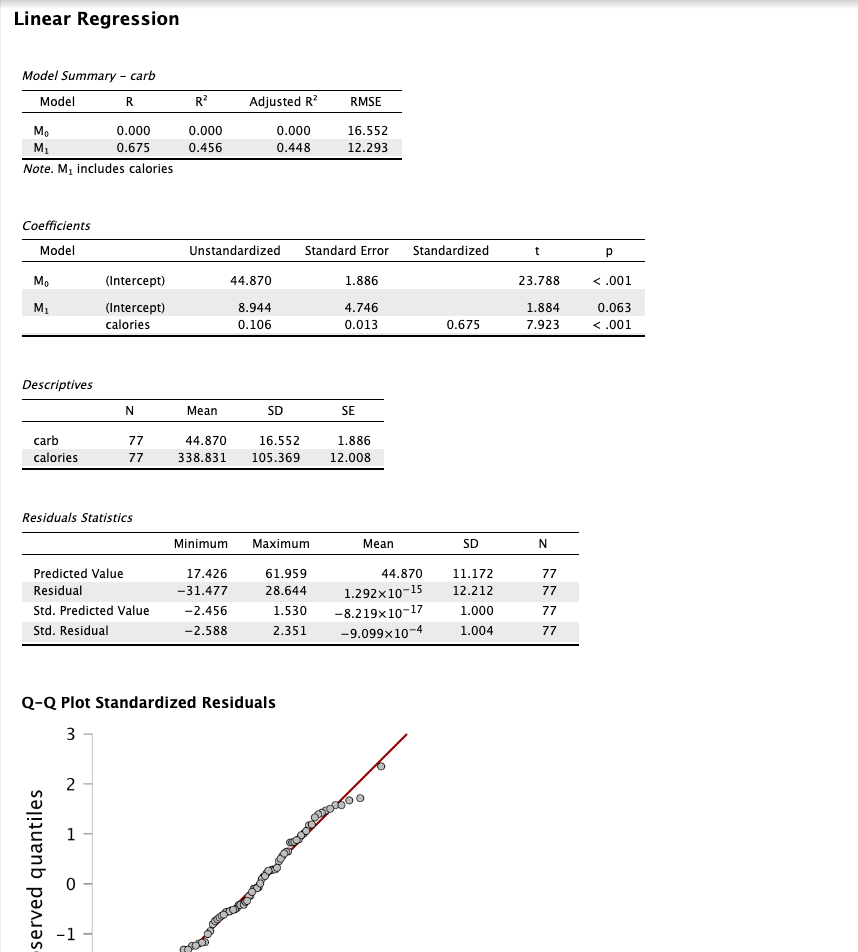Linear Regression
Figure 2: Linear regression between calories and carbs (1).
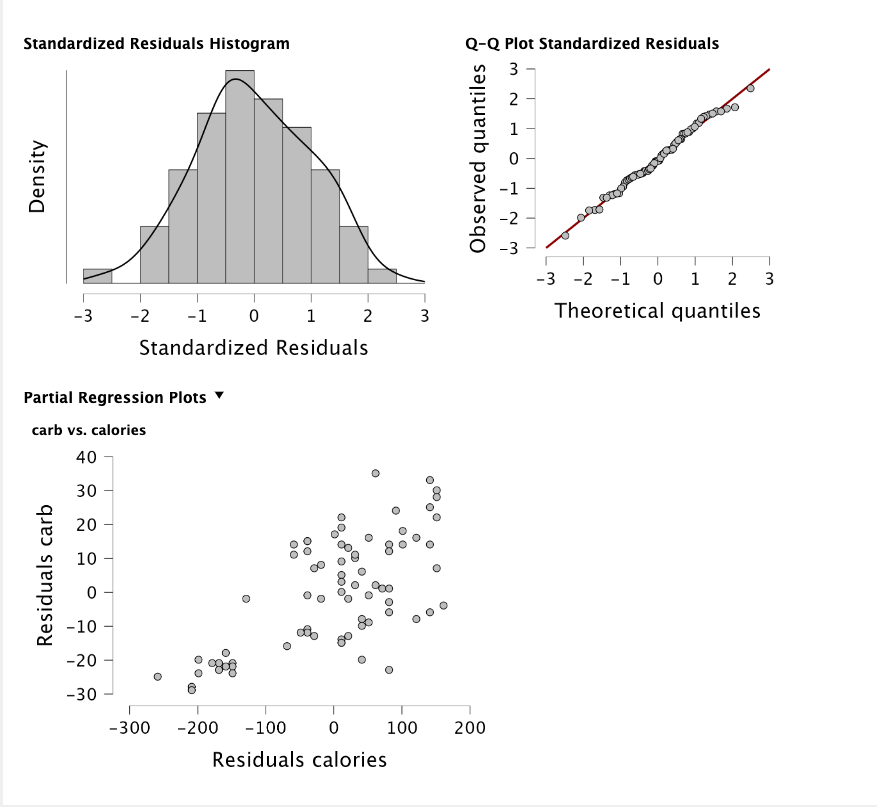Linear Regression
Figure 3: Linear regression between calories and carbs (2).

1. What is the correlation coefficient (Pearson’s r) between the variable’s calories and carb?

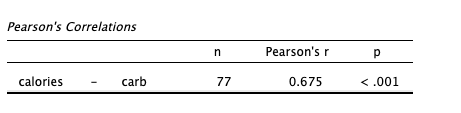Pearson Correlation
Figure 4: Pearson correlation between calories and carbs.

The correlation coefficient (Pearson’s r) between the variables calories and carbs is 0.675.

2. Interpret the strength of the relationship between the calories and the amount of carbohydrates (in grams) contained in the food menu at Starbucks

The value of the correlation coefficient (Pearson’s r) is 0.675; which is between 0.4 and 0.8. This value indicates a moderate positive relationship between the number of calories and the amount of carbohydrates, that is, as the grams of carbohydrates increase, the number of calories moderately increases.

3. Using JASP descriptive statistics, find the mean and standard deviation for the variable calories and carb

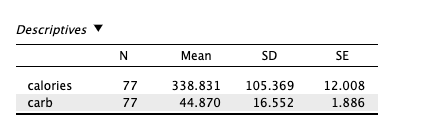Descriptive Statistics
Figure 5: Descriptive statistics.
  • For calories, the mean is 338.831 and the standard deviation is 105.369.
  • For carbs, the mean is 44.870 and the standard deviation is 16.552.

4. Write the equation of the regression line for prediction of the amount of carbohydrates given the number of calories

We calculate the slope (b1), using information from the previous steps:

\[ \begin{aligned} b_1 &= r ⋅ \frac{s_y}{s_x} \\ &= r \cdot \frac{s_{carbs}}{s_{calories}} \\ &= 0.675 * \frac{16.552}{105.369} \\ &= 0.106 \end{aligned} \]

Next, we calculate the intercept (b0):

\[ \begin{aligned} b_0 &= \bar{y} - b_1 \cdot \bar{x} \\ &= \bar{carbs} - b_1 \cdot \bar{calories} \\ &= 44.870 - (0.106 \cdot 338.831) \\ &= 8.953 \end{aligned} \]

The regression equation is:

\[ \text{Carbs} = 0.106 \cdot \text{Calories} + 8.953 \text{ ____(1)}\\ \]

5. Using JASP linear regression, validate the regression equation found in c

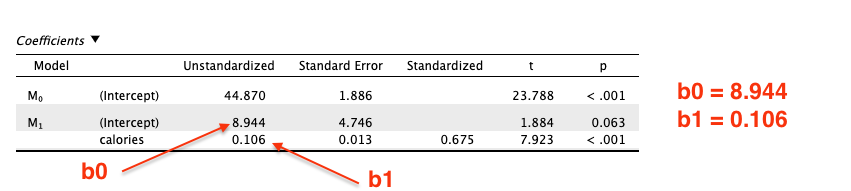Regression Equation
Figure 6: Regression equation coefficients.
  • The slope is b1 = 0.106.
  • The intercept is b0 = 8.944.
  • The regression equation is y = 0.106x + 8.944.

The final equation from the JASP output is:

\[ \text{Carbs} = 0.106 \cdot \text{Calories} + 8.944 \text{ ____(2)}\\ \]

By comparing with the equation (1) that we computed manually in the previous step, we can see that the values are the same (with a small rounding difference in the intercept).

By similarity of the equations, JASP validates the regression equation found in c.

6. Calculate R2 of the regression line for predicting the amount of carbohydrates from the number of calories and interpret it in the context of the application

R2
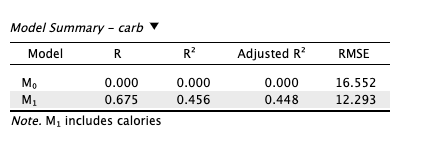Figure 7: R2 value.

R^2 = (0.675)^2 = 0.455625 (also shown in Figure 7).

The R^2 value is 0.455625. This means that 45.56% of the variation in the amount of calories can be explained by the number of carbs. This indicates that the model is a moderate fit for the data, and the number of calories can moderately predict the amount of carbohydrates in the food menu at Starbucks, while there are other factors that contribute to 55% of the variation in the amount of carbohydrates.

References