Written Assignment 1

Question 1

1. What linear function, y=f(x) has f(0) = 8 and f(7) = 14 ?

$$\begin{gathered} y=mx+b\text{ --------(1)} \\ 14=m(7)+b\text{ --------(2)} \\ 8=m(0)+b\text{ --------(3)} \\ \text{From (2) and (3), we find m} \\ m=\frac{14-8}{7-0}=\frac{6}{7} \\ \text{substitute m into (2)} \\ 14=\frac{6}{7}(7)+b \\ 14=6+b \\ b=8 \\ \text{substitute m and b into (1) which is the final solution} \\ y=\frac{6}{7}x+8 \end{gathered}$$

---

Question 2

2. If $f(t)=2t-t^2+3$ , what is $\frac{f(t+h)-f(t)}{h}$ ?

Let’s find f(t+h)

$$\begin{gathered} f(t+h)=2(t+h)-(t+h{)}^2+3 \\ f(t+h)=2t+2h-(t^2+2th+h^2)+3 \\ f(t+h)=2t+2h-t^2-2th-h^2+3 \end{gathered}$$

And then substitute f(t+h) and f(t) into the equation

$$\begin{array}{rl}\frac{f(t+h)-f(t)}{h}& =\frac{2t+2h-t^2-2th-h^2+3-(2t-t^2+3)}{h}\\ & =\frac{2t+2h-t^2-2th-h^2+3-2t+t^2-3}{h}\\ & =\frac{2h-2th-h^2}{h}\\ & =\frac{h(2-2t-h)}{h}\\ & =2-2t-h\end{array}$$

---

Question 3

3. Find all solutions to the equation $-4cosx=-si{n}^{2}x+1$. Write your answer in radians in terms of $\pi$

we know that $si{n}^{2}x=1-co{s}^{2}x$, so we can use it in the equation

$$\begin{array}{rl}-4cosx& =-si{n}^{2}x+1\\ -4cosx& =-(1-co{s}^{2}x)+1\\ -4cosx& =-1+co{s}^{2}x+1\\ -4cosx& =co{s}^{2}x\\ co{s}^{2}x+4cosx& =0\\ cosx(cosx+4)& =0\end{array}$$

The equation is true when $cosx=0$ or $cosx=-4$

• $x=-4$ is refused as it is not in the domain of $cosx$ which is $[-1,1]$.
• $x=0$ is accepted.

So for $cos(x)=0$ we have $x=\frac{\pi }{2}+\pi n$ where $n$ is an integer.

---

Question 4

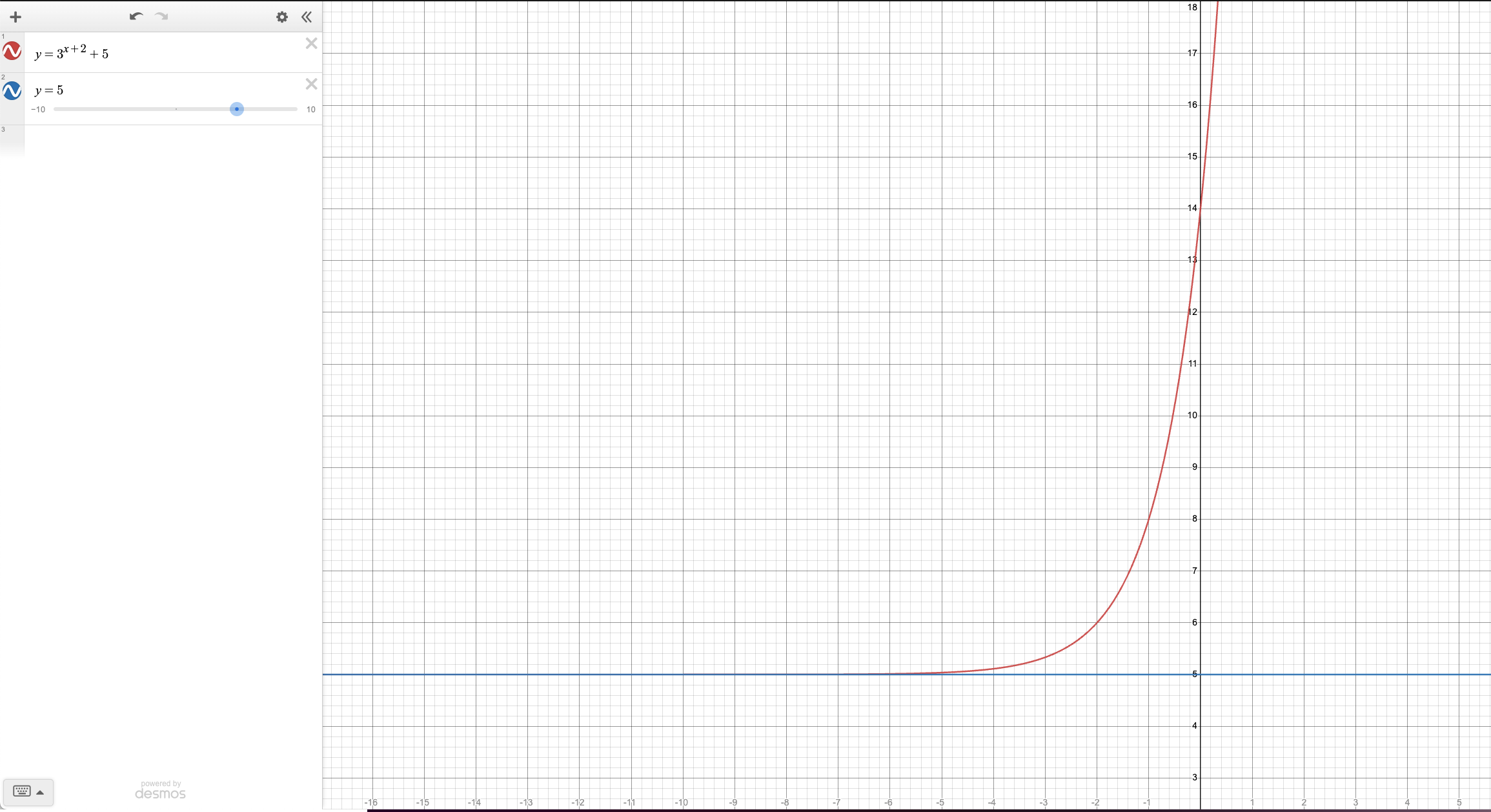
4. Sketch the graph of $y=3^{x+2}+5$. Find the domain, range, and horizontal asymptote. Include the horizontal asymptote in your graph.

• The domain is $(-\mathrm{\infty },\mathrm{\infty })$ as there is no restriction on the value of $x$.
• The range is $(5,\mathrm{\infty })$. as the term $3^{x+2}$ is always positive and $5$ is added to it.
• The line $y=5$ is the horizontal asymptote (colored blue in the graph below) as $x$ approaches $-\mathrm{\infty }$ the value of $y$ approaches $5$.

---

Question 5

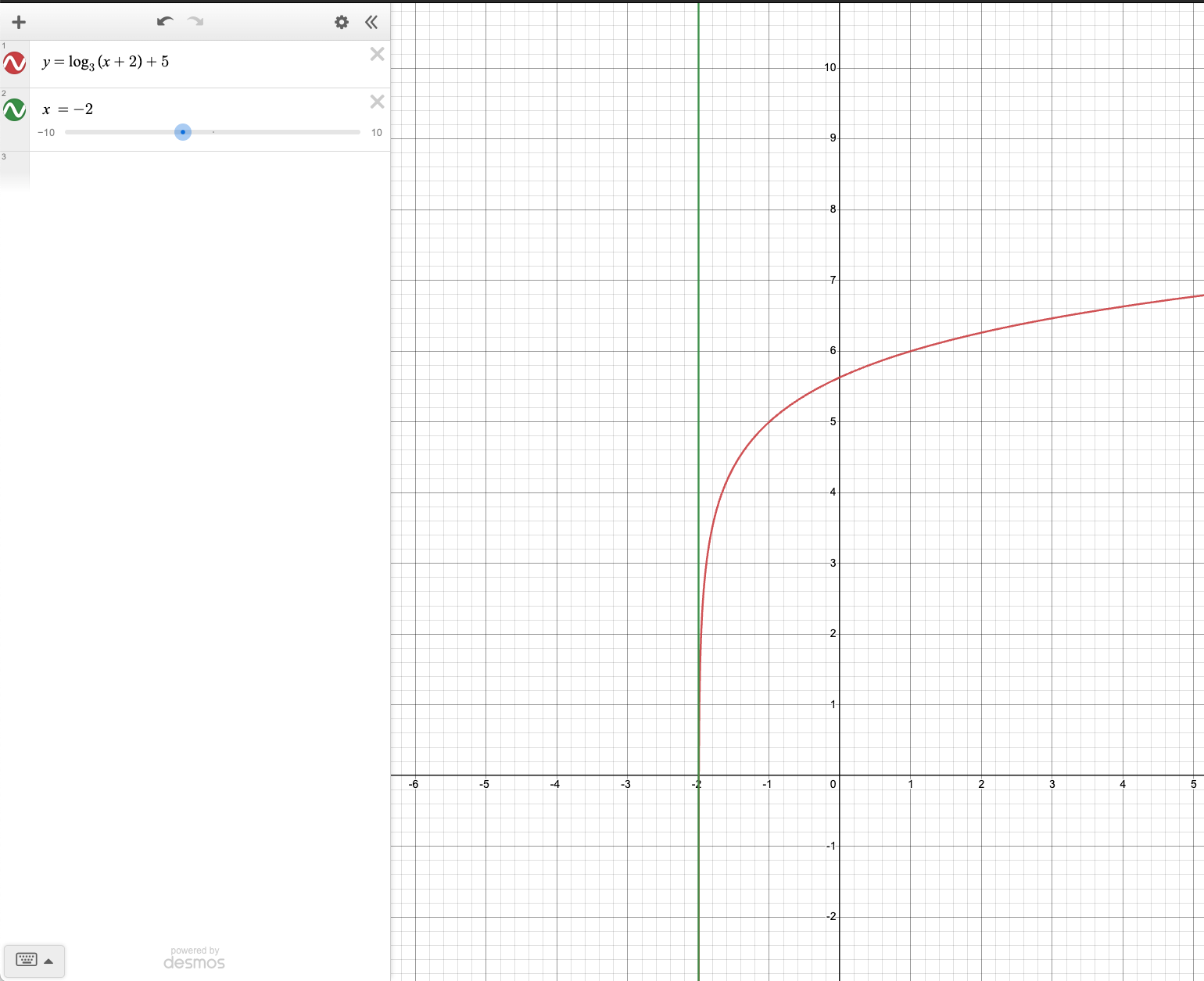
5. Sketch the graph of $y=log\mathrm{\_}3(x+2)+5$. Find the domain, range, and vertical asymptote. Include the vertical asymptote in your graph.

• The domain is $(-2,\mathrm{\infty })$ as $x+2$ must be positive (as it is the argument of the logarithm function).
• The range is $(-\mathrm{\infty },\mathrm{\infty })$ as the logarithm function can take any value.
• The line $x=-2$ is the vertical asymptote (colored green in the graph below) as $x$ approaches $-2$ the value of $y$ approaches $-\mathrm{\infty }$.

---

Question 6

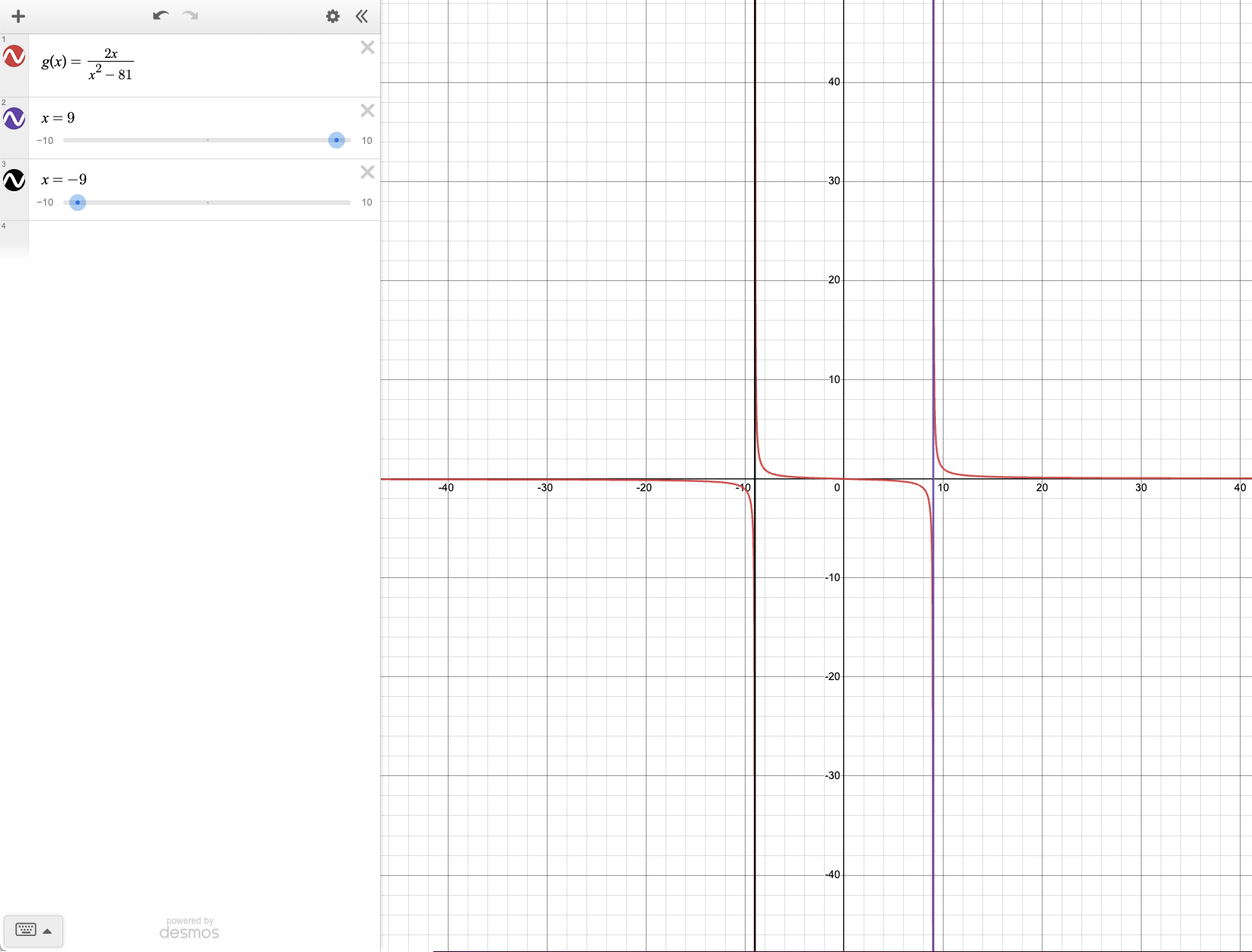
6. Find the domain fo the function $g(x)=\frac{2x}{x^2-81}$.

The function is defined for all values of $x\in \mathbb{R}$ except when the denominator is zero. So we need to find the values of $x$ for which $x^2-81=0$ which is solved for $x=\pm 9$.

So the domain is $(-\mathrm{\infty },-9)\cup (-9,9)\cup (9,\mathrm{\infty })$ or $\mathbb{R}-\{-9,9\}$.

---

Question 7

7. From the graph below, find what is f(-15) and for what numbers x is f(x)=0.

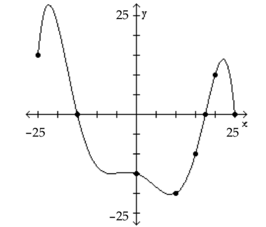
• $f(-15)=0$ as the graph crosses the x-axis at $x=-15$.
• $f(x)=0$ when $x=-15$ and $x=17$ as the graph crosses the x-axis at $x=-15$ and $x=17$.

---

Question 8

8. Determine whether the graph is that of a function. If it is, use the graph to find its domain and range, the intercepts, if any, and any symmetry with respect to the x-axis, the y-axis, or the origin.

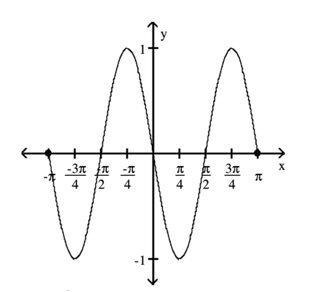
• The graph is function as for each value of $x$ there is only one value of $y$.
• The domain is $(-\mathrm{\infty },\mathrm{\infty })$ as there is no restriction on the value of $x$.
• The range is $[-1,1]$ as the value of $y$ is always between -1 and 1.
• The graph crosses the x-axis 5 times each period. So the x-intercepts in the period shown in the graph are $x=-\frac{3}{2},-\frac{1}{2},0,\frac{1}{2},\frac{3}{2}$.
• Symmetry with respect to the y-axis as the graph is symmetric about the y-axis and origin.
• No symmetry with respect to the x-axis.

---

Question 9

9. Determine whether the function is even, odd, or neither.

a. $f(x)=4x^3$ b. $f(x)=\frac{-x^3}{4x^2+3}$ c. $f(x)=3x^3-5$

A function is even if $f(-x)=f(x)$ and odd if $f(-x)=-f(x)$..

a. $f(x)=4x^3$ is odd.

$$\begin{array}{rl}f(-x)& =4(-x{)}^3\\ & =-4x^3\\ & =-f(x)\end{array}$$

b. $f(x)=\frac{-x^3}{4x^2+3}$ is odd.

$$\begin{array}{rl}f(-x)& =\frac{-(-x{)}^3}{4(-x{)}^2+3}\\ & =\frac{-(-x{)}^3}{4x^2+3}\\ & =-\frac{-x^3}{4x^2+3}\\ & =-f(x)\end{array}$$

c. $f(x)=3x^3-5$ is neither.

$$\begin{array}{rl}f(-x)& =3(-x{)}^3-5\\ & =-3x^3-5\\ & \ne -f(x)\\ & \ne f(x)\end{array}$$

---

Question 10

10. A cellular phone plan had the following schedule of charges: Basic service, including 100 minutes of calls is $20.00/month; 2^nd 100 minutes of calls is $0.075/minute; additional minutes of calls is $0.10/minute.

a. What is the charge for 200 minutes of calls in one month?

• The first 100 minutes are included in the basic service ($20.00/month).
• The next 100 minutes are charged at $0.075/minute($0.075 × 100 = 7.50$).
• Thus, the charge for 200 minutes is $20.00+7.50=27.50$.

b. What is the charge for 250 minutes of calls in one month?

• The first 100 minutes are included in the basic service ($20.00/month).
• The next 100 minutes are charged at $0.075/minute($0.075 × 100 = 7.50$).
• The next 50 minutes are charged at $0.10/minute($0.10 × 50 = 5.00$).
• Thus, the charge for 250 minutes is $20.00+7.50+5.00=32.50$.

c. Construct a function that relates the monthly charge C for x minutes of calls?

$$C(x)=\{\begin{array}{ll}20,& \text{if }x\le 100\\ 20+0.075(x-100),& \text{if }100<x\le 200\\ 20+0.075\times 100+0.10(x-200),& \text{if }x>200\end{array}$$