DA5. Non Binary Trees¶
Code¶
import jeliot.io.*;
class Node {
Node left;
Node right;
int value;
public Node(int value) {
this.value = value;
}
}
public class GeneralTreeTest {
public static void main(String[] args) {
// build a simple tree add 5 nodes to the tree
Node root = new Node(5);
System.out.println("Tree Example");
System.out.println("Building tree with root value " + root.value);
insert(root, 1);
insert(root, 8);
insert(root, 6);
insert(root, 3);
insert(root, 9);
System.out.println("Traversing tree ");
printOrder(root);
}
public static void insert(Node node, int value) {
if (value < node.value) {
if (node.left != null) {
insert(node.left, value);
} else {
System.out.println(" Inserted " + value + " to left of " + node.value);
node.left = new Node(value);
}
} else if (value > node.value) {
if (node.right != null) {
insert(node.right, value);
} else {
System.out.println(" Inserted " + value + " to right of " + node.value);
node.right = new Node(value);
}
}
}
public static void printOrder(Node node) {
if (node != null) {
printOrder(node.left);
System.out.println(" Traversed " + node.value);
printOrder(node.right);
}
}
}
Statement¶
This algorithm first inserts five nodes into a tree structure and then traverses the tree.
- Using the Jeliot environment, load, compile and execute this java algorithm to understand its operation.
- Determine the kind of tree structure that is being created and determine what kind of traversal the algorithm is conducting.
- Finally, conduct an Asymptotic analysis for the provided algorithm and report your analysis including Big O, Big Omega, or Big Theta as appropriate.
Solution¶
1. Using the Jeliot environment, load, compile and execute this java algorithm to understand its operation¶
- The result of executing the code in the Jeliot environment is shown below:
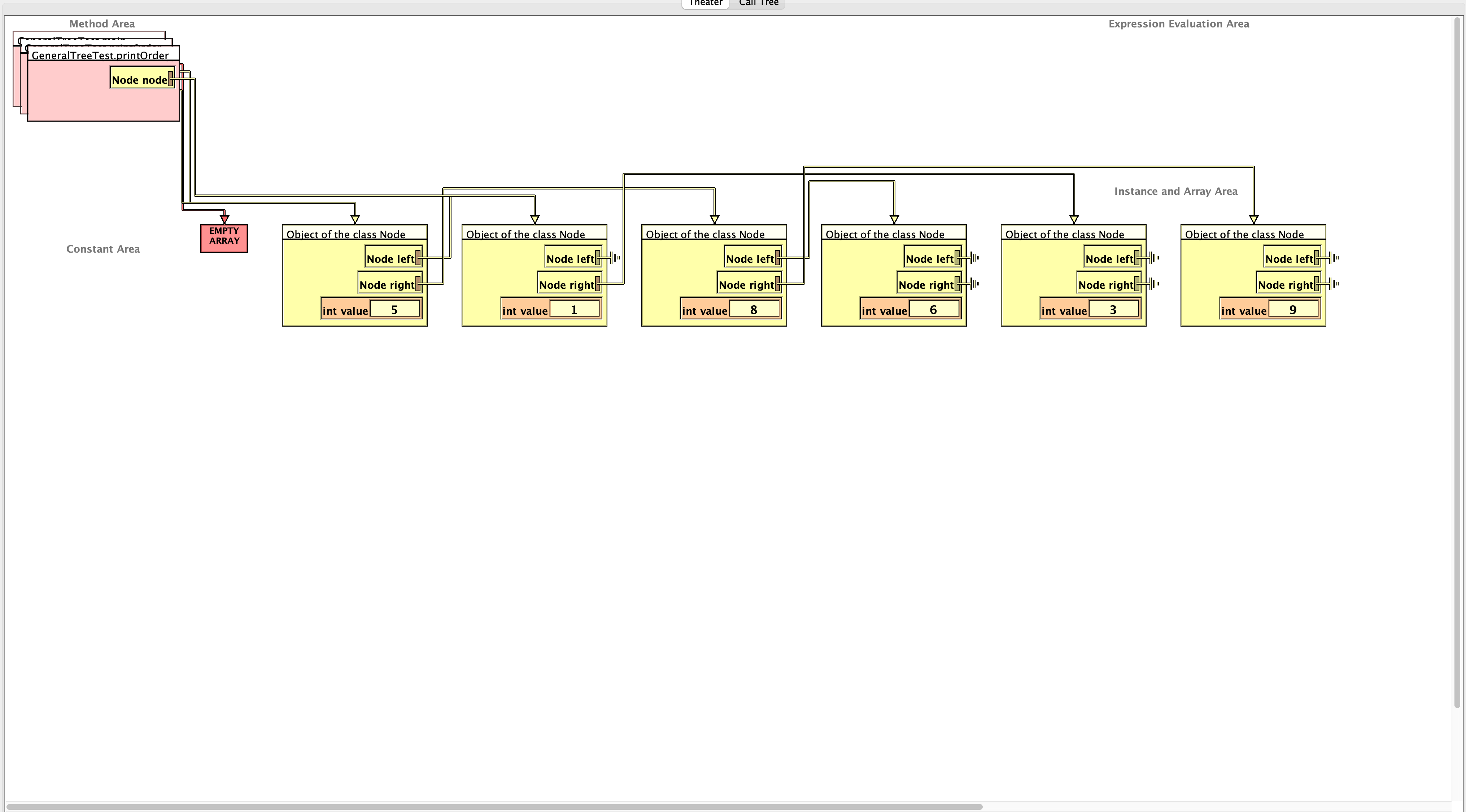
2. Determine the kind of tree structure that is being created and determine what kind of traversal the algorithm is conducting¶
- The tree structure being created is a binary search tree.
- We conclude this due to two facts:
- The node class only maintains two pointers, one for the left child and one for the right child.
- The algorithm is inserting node that are smaller than the current node to the left, while nodes that are larger than the current node are inserted to the right.
- The above two facts conforms with the binary search tree definition, and thus we conclude that the tree structure being created is a binary search tree.
-
Note that
insertfunction only handles the cases where the new value is greater or less than current node, it does not handle the case where the new value is equal to the current node. This is because the algorithm is not inserting duplicate values into the tree, and just ignores them. -
The algorithm is conducting an in-order traversal as it is traversing the left subtree first, then the root, and then the right subtree.
- We can confirm that by checking the traverse log which prints the values in a ascending order.
3. Finally, conduct an Asymptotic analysis for the provided algorithm and report your analysis including Big O, Big Omega, or Big Theta as appropriate¶
Asymptotic Analysis of the traverse function¶
- The
traversefunction is pretty straightforward, it visits every node in the tree exactly once, thus its upper and lower bounds are the same. - Hence, the
traversefunction has a linear time complexity ofO(n),Ω(n), andΘ(n)wherenis the number of nodes in the tree.
Asymptotic Analysis of the insert function¶
- The
insertfunction is a bit more complicated, as it depends on the order that the values are inserted into the tree. - The lower bound achieved when the values are inserted in a random order, as the tree will be balanced and the height of the tree will be
log(n). - The upper bound is achieved when the values are inserted in a sorted order, as the tree will be unbalanced and the height of the tree will be
n(almost a linked list), and all values are inserted to one branch of the tree (either left or right). - If the inserted values are sent in an ascending order, the tree will have only a right branch, and internal node will have only one right child which makes the space for the left child wasted.
- The opposite is true if the inserted values are sent in a descending order, the tree will have only a left branch, and internal node will have only one left child which makes the space for the right child wasted.
- The time complexity for the lower bound is
Ω(log(n)), while the time complexity for the upper bound isO(n). - Since the lower bound and upper bound are different, the average case is somewhere in between, and is closer to the lower bound and we can conclude that the time complexity of the
insertfunction isΘ(log(n)).
References¶
- Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf. Chapter 5.
- Barnett, G. & Del Tongo, L. (2008). Data Structures and Algorithms: An Annotated Reference with Examples. Chapter 3: Binary Search Tree.