Skip to content

2. Divide and Conquer Algorithms

  • Abbreviations:
    • DAC: Divide and Conquer.

Introduction 1

  • We know that an upper bound is the worst case scenario of resource consumption that is consumed with the best algorithm that we have for a particular problem.
  • We also know that a lower bound is the best case scenario of resource consumption that is consumed with the best algorithm that we have for a particular problem.
  • In a linear search on a unsorted list with a length of n, the upper bound is O(n) and the lower bound is Ω(1). Best case is the first element in the list and the worst case is the last element in the list.
  • If there is a great difference between the upper bound and the lower bound, then we can say that we have not found the best algorithm for that problem and the algorithm is not efficient.
  • The ‘tighter’ the bounds or the closer that the upper bound is to the lower bound, the more efficient the algorithm.
  • In fact we learn that when the upper bound and lower bound are the same then the algorithm cannot become any more efficient.
  • The text defines an algorithm as a ‘good’ algorithm when the upper bound and lower bound are the same asymptotically.
  • Amortized analysis refers to determining the time-averaged running time for a sequence of operations.
  • It is different from what is commonly referred to as average case analysis, because amortized analysis does not make any assumption about the distribution of the data values, whereas average case analysis assumes the data are not “bad”.
  • Amortized analysis is a worst case analysis, but for a sequence of operations, rather than for individual operations. It uses the fact that we are analyzing a sequence to “spread out” the cost.
  • The general approach is to assign an artificial cost to each operation in the sequence, such that the total of the artificial costs for the sequence of operations bounds total of the real costs for the sequence.
  • This artificial cost is called the amortized cost of an operation.
  • There are several approaches commonly used for amortized analysis however we will look at two in particular including the aggregate method and the banker’s method (tokens).
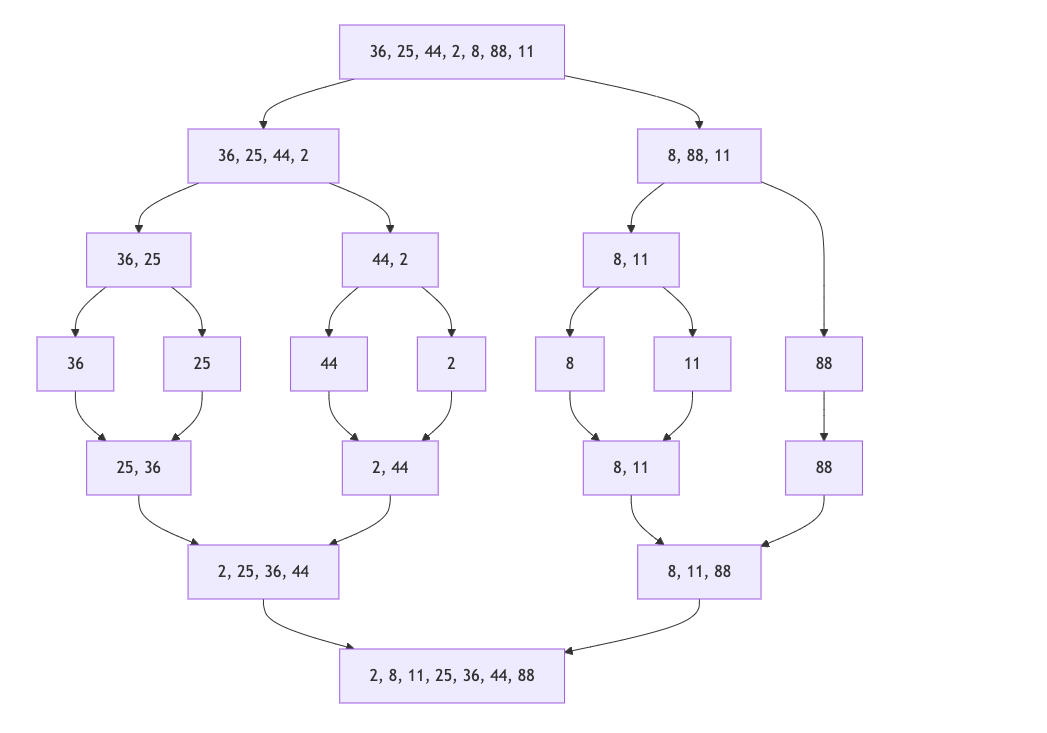
  • Divide and conquer algorithms use the following three phases:
    1. Divide the problem into smaller sub-problems. A sub-problem of a problem is a smaller input for the same problem. The input for the subproblem is a subset of the original input, but that need not be the case.
    2. Conquer by recursively solving the subproblems (unless the problem size has reached a specified termination condition).
    3. Combine the solutions to the subproblems to obtain the solution for the original problem.
  • The real magic is in the combining, and finding the right subproblems to recursively solve.

Lec 13 | MIT 6.046J / 18.410J Introduction to Algorithms (SMA 5503), Fall 2005 3

  • Hash tables:
    • If the table is as large as possible, then every element can be put/searched in O(1) time, as every hash list will have only one element (or small number of elements).
    • The table above requires large space, but the time complexity is good.
  • Dynamic tables:
    • It solves the problem of not knowing the size of the hash table in advance.
    • Every time the table is full, a new table is created with double the size of the previous table, and all elements are rehashed.
    • that is, copying the table in a new table that is twice the size of the previous table.
  • Amortized analysis for dynamic tables:
    • The copying process in the expensive operation, but in a sequence of insertions, we only need to copy the table if the table size is a power of 2.
    • If we spread the cost of copying the table over the next insertions, then there will be a small cost for each insertion.
    • The cost of one insertion (worst case) is O(n) without amortized analysis: copy the previous n elements and insert the new element.
    • Using amortized analysis, the average cost for each insertion is O(n)/n = O(1).
    • This analysis is aggregate analysis.
  • Methods of amortized analysis:
    • Aggregate method:
      • The cost of the sequence is summed up and then the average cost is calculated.
      • The average cost is assumed for all operations in the sequence.
    • Accounting method:
      • Each operation is charged an amortized cost in dollars ($).
      • When doing the analysis, if an operation does not use all of its allocated dollars, then the remaining dollars are stored in the bank, and can be used to pay future operations.
      • if bank balance does not go negative, then the amortized cost is good.
    • Potential method:
      • The bank concept in the accounting method is replaced with a potential energy concept.
      • Every operation is determined by a function that takes the previous state of the data structure and return the new state after the operation. Op: S -> S’.
      • We define a potential function Φ(S) that maps the state of the data structure to a real number.

Lower Bounds 4

Divide-and-conquer Algorithms 5 2

Lec 10 | MIT 6.00 Introduction to Computer Science and Programming, Fall 2008 7

  • The series of operations covered in amortized analysis may include repeated searches, that is, if I have to do multiple searches on a unsorted list, it would be better to sort it first (expensive operation), and then do the searches (cheaper operations).
  • For searching in unsorted lists:
    • We need to use linear search which costs O(n).
    • For a k number of searches, the cost would be O(kn).
    • If we sort the list first, then we can use binary search which costs O(log n), however, sorting the list is O(n log n).
    • Hence, a single sort + search would cost O(n log n + log n).
    • But for k number of searches, the cost would be O(n log n + k log n) which is better than O(kn).
    • This is an example of amortized analysis where the sort operation O(n log n) is far more expensive than the search operation O(log n), but the cost of the sort operation is spread out over the k searches.
  • Good candidates for divide and conquer algorithms:
    • Problems that can be broken down into smaller subproblems.
    • Problems that can be solved recursively.
    • Problems that can be combined to solve the original problem with as little effort as possible. If the combine process is too expensive, then DAC is not efficient.
  • Usually, gains in time complexity require losses in space complexity and vice versa; aka, we trade tim for space and vice versa.
  • It is hard to create a good hashing function, because it is hard to create a function that maps a large set of inputs to a small set of outputs without collisions, and divide the hashes evenly.

Unit 2 Lecture 1: Amortized Analysis 8

  • Amortized analysis is a method for analyzing the time complexity of algorithms that perform a sequence of operations to show that the average time per operation is small, even though a single operation within the sequence may be expensive.
  • Amortized analysis guarantees the average performance of each operation in the worst case.
  • Formal schemes for amortized analysis:
    • Aggregate method: The total cost of a sequence of operations is analyzed.
    • Accounting method: Each operation is charged an amortized cost.
    • Potential method: The potential function is used to determine the amortized cost of each operation.
  • Aggregate method:
    • Find the upper bound on the total cost of a sequence of operations (worst-case cost), denote it by T(n).
    • Find average cost per operation, T(n)/n which is the amortized cost.
    • This amortized cost is assumed for each operation in the sequence, regardless of the actual cost of the operation.

Unit 2 Lecture 2: Estimating Upper and Lower Bounds 9

  • Upper bound is the maximum time complexity of an algorithm in the worst-case scenario.
  • Lower bound is the minimum time complexity of an algorithm in the best-case scenario.
  • On average, the time complexity of an algorithm is between the upper and lower bounds.
  • Tight and loose bounds:
    • Tight bounds (asymptotically tight) refer to the exact asymptotic growth of an algorithm’s complexity, represented using Θ (Theta) notation.
    • Loose bounds are broader approximations using O (Big-O) or Ω (Omega) notation but without matching both upper and lower bounds closely.
    • For example, tight upper bound is O(n), but loose upper bound is O(n^2), O(n^3), ... or any O notation that is greater than O(n).
    • Another example, tight lower bound is Ω(n), but loose lower bound is Ω(log n), Ω(1), ... or any Ω notation that is less than Ω(n).
    • The goal is to find the tightest bounds for the time complexity of an algorithm.
  • bounds
  • In the image above:
    • Blue line represents the upper bound Big-O notation.
    • Green line represents the lower bound Big-Omega notation.
    • Purple line represents the actual time complexity of the algorithm.
    • Notice before N0:
      • The actual time complexity is above both the upper and lower bounds.
      • The actual time complexity is below both the upper and lower bounds.
    • We are not interested in the area before N0, because n is too small to be significant.
    • We are interested in the right area of the chart as n grows larger.

Unit 2 Lecture 3: Divide and Conquer Algorithms 10 6

  • Divide and conquer:
    • Divide: Break the problem into smaller subproblems.
    • Conquer: Solve the subproblems recursively.
    • Combine: Combine the solutions to the subproblems to solve the original problem.
  • Examples of divide and conquer algorithms:
    • Binary search.
    • Merge sort.
    • Quick sort.
    • Strassen’s matrix multiplication.
    • Closest pair of points.

Reference

  1. Learning Guide Unit 2: Introduction | Home. (2025). Uopeople.edu. https://my.uopeople.edu/mod/book/view.php?id=453887&chapterid=554093 ↩

  2. Read Chapter 2, section 2.2. Divide-and-conquer Algorithms in Algorithms by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani available at: http://www.cs.berkeley.edu/~vazirani/algorithms/chap2.pdf ↩

  3. Amortized Analysis, By Charles E. Leiserson - MIT (at 19:05 minutes) https://www.youtube.com/watch?v=qh5lSHCBiRs ↩

  4. Chapter 15: Lower Bounds, in A Practical Introduction to Data Structures and Algorithm Analysis by Clifford A. Shaffer. ↩

  5. Read Chapter 2 Divide-and-conquer Algorithms in Algorithms by S. Dasgupta, C.H. Papadimitriou, and U.V. Vazirani available at http://www.cs.berkeley.edu/~vazirani/algorithms/chap2.pdf ↩

  6. Santa’s Dirty Socks (Divide and Conquer Algorithms) (2024). Youtube.com. https://www.youtube.com/watch?v=wVPCT1VjySA&t=1s ↩

  7. Lec 10 | MIT 6.00 Introduction to Computer Science and Programming, Fall 2008. (2024). Youtube.com. https://www.youtube.com/watch?v=kDhR4Zm53zc ↩

  8. ‌Unit 2 Lecture 1: Techniques for the Analysis of Algorithms ↩

  9. Unit 2 Lecture 2: Estimating Upper and Lower Bounds ↩

  10. Unit 2 Lecture 3: Divide and Conquer Algorithms ↩