5. Power calculations and ANOVA¶
7.4 Power calculations for a difference of means 1¶
7.5 Comparing many means with ANOVA 1¶
Descriptive Statistics & ANOVA 2¶
Power calculations for a difference of two means 3¶
- In clinical trials, researchers often want to know how many participants they need to recruit to detect a difference between two groups.
- Because of the sensitivity of the test, the sample size is crucial.
- Collecting data is expensive and time-consuming, and there is some risk of harm to participants.
- We should be at least 80% confident that we will detect a difference if one exists.
- Power is the probability of correctly rejecting the null hypothesis when the alternative hypothesis is true. It is
1-β, whereβis the probability of a Type II error. - If type 2 error is low, power is high.

- We want to keep both
αandβlow, but reducing one increases the other, so the solution is to increase the sample size. - We can find the standard error of the difference between two means by using the formula
SE = sqrt((s1^2/n1) + (s2^2/n2)). - Then we use normal distribution to find the critical value, mean = 0, and standard deviation =
SE. - To find the sample size for 80% power, we use the formula
n = (Zα/2 + Zβ)^2 * (s1^2 + s2^2) / (μ1 - μ2)^2. 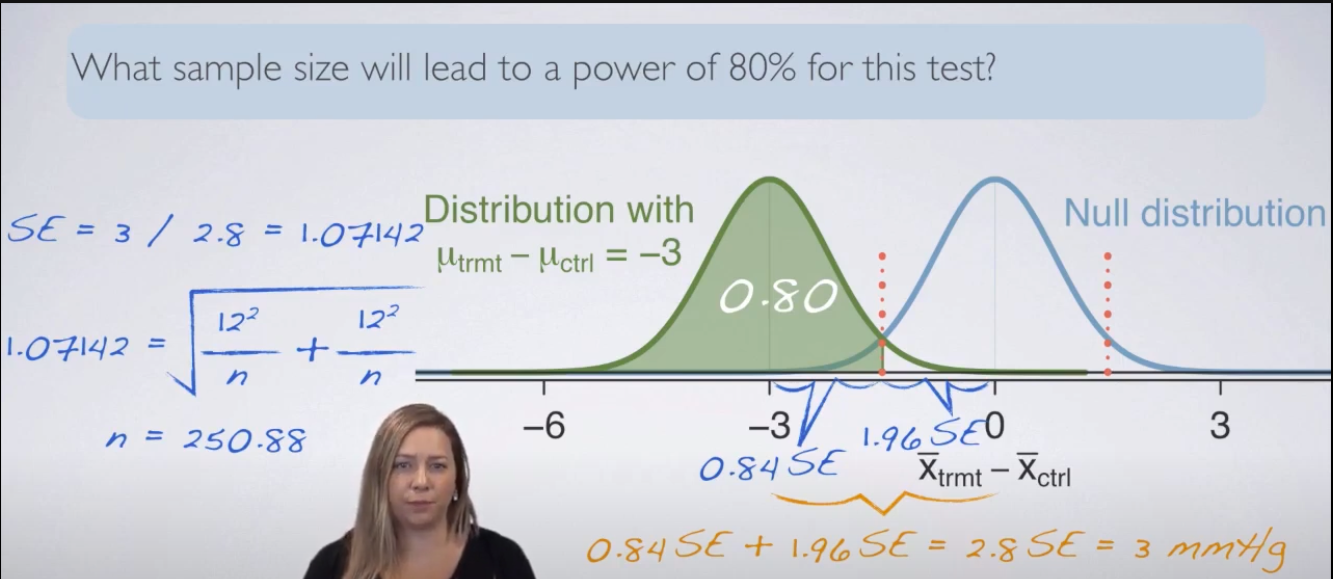
ANOVA introduction 4¶
- ANOVA stands for Analysis of Variance.
- Total variability in the data can be broken down into two parts: variability between groups and variability within groups.
- Between-group variability: Variability in the data that is due to the different groups (variability between different groups).
- Within-group variability: Variability in the data that is due to the differences within each group (variability between different observations within the same group).
- Anova output table:
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | ||
|---|---|---|---|---|---|---|
| Group | Between group variable (Class) | DFG | SSG | MSG | F | P-value |
| Error | within group variability (Residual) | DFE | SSE | MSE | ||
| Total | DFT | SST |
- SST:
- Sum of squares total.
- Captures the total variability in the data.
- Similar to computing the
varianceof the data, but it is not scaled by the sample size. - \(SST = \sum_{i=1}^{n} (y_{i} - \bar{y})^2\).
- \(y\) value of the variable for each observation.
- \(\bar{y}\) is the overall mean of all observations.
- SSG:
- Sum of squares groups.
- Captures the variability between groups, that is, the variability in the data that is due to variable in question.
- The explained variability in the data, the variability that is explained by the variable in question.
- Calculated as the squared deviation of group means from the overall mean, weighted by the number of observations in each group.
- It is not interesting in its own, but it is useful when compared to SST.
- The percentage
(SSG/SST)is the proportion of variability that is attributed to the variable in question, while1-(SSG/SST)is the proportion of variability that is attributed to all other sources. - \(SSG = \sum_{j=1}^{k} n_{j} (\bar{y}_{j} - \bar{y})^2\).
- \(n_{j}\) is the number of observations in group \(j\).
- \(\bar{y}_{j}\) is the mean of group \(j\).
- \(\bar{y}\) is the overall mean.
- SSE:
- Sum of squares error.
- Captures the variability within groups, that is, the variability in the data that is due to all other variables but the variable in question.
- The unexplained variability in the data, the variability that is not explained by the variable in question.
- Calculated as the squared deviation of each observation from its group mean.
- $SSE = SST - SSG $.
- DFT:
- Degrees of freedom total.
- The number of observations minus one.
- \(DFT = n - 1\).
- \(n\) is the sample size.
- DFG:
- Degrees of freedom groups.
- The number of groups minus one.
- \(DFG = k - 1\).
- \(k\) is the number of groups within the variable in question.
- DFE:
- Degrees of freedom error.
- The number of observations minus the number of groups.
- \(DFE = DFT - DFG = n - k\).
- MSG:
- Mean squares groups.
- The average variability between groups.
- \(MSG = SSG / DFG\).
- MSE:
- Mean squares error.
- The average variability within groups.
- \(MSE = SSE / DFE\).
- F:
- F statistic.
- The ratio of the variability between groups to the variability within groups.
- \(FT = MSG / MSE\).
- Pr(>F):
- P-value.
- The probability of observing the data if the null hypothesis is true.
- If the p-value is less than the significance level, we reject the null hypothesis.
- If the p-value is greater than the significance level, we fail to reject the null hypothesis.
- It is the probability of at least as large a ratio between the “between” and “within” group variabilities if in fact, the means of the groups are the equal (null hypothesis is true).
- It is the area to the right of the observed F value under the F distribution with DFG and DFE degrees.
- F-distribution is a right-skewed distribution, and always positive.
Conditions for ANOVA 5¶
- Independence:
- Observations within each group are independent.
- Random sample / random assignment.
- Each group size is less than 10% of the population size.
- It is important, but it is difficult to check.
- Observations between groups are independent:
- Groups are independent of each other (not paired).
- If data is paired, use the repeated measures ANOVA.
- Observations within each group are independent.
- Approximate normality:
- The distribution of the response variable is approximately normal within each group.
- It is especially important when the sample size is small.
- Equal variance:
- The variability of the response variable is approximately the same within each group.
- Variability should be consistent across groups, that is, homoscedastic groups.
- It is important if the sample size differs between groups.
JASP ANOVA 6¶
- Load the data from the file.
- Make sure the variable in question is of type
ratio scale. - Choose
Descriptive Statisticsfrom theAnalysismenu. - Select the variable in question.
- Select the following:
- Display frequency tables.
- Display the median.
- Select
ANOVAfrom theAnalysismenu.- Under additional options, select:
- Descriptive statistics.
- Effect size (partial eta \(\eta^2\) squared).
- Under additional options, select:
- In
Fixed Factors, select two or more variables ofnominal scale, they will be used as predictor variables. - Select the variable in question as the
dependent variable.
References¶
-
Diez, D. M., Barr, C. D., & Çetinkaya-Rundel, M. (2019). Openintro statistics - Fourth edition. Open Textbook Library. https://www.biostat.jhsph.edu/~iruczins/teaching/books/2019.openintro.statistics.pdf Read Chapter 7 - Inference for numerical data Section7.4 - Power calculations for a difference of means from page 278 to page 284 Section 7.5 - Comparing many means with ANOVA from page 285 to page 302 ↩↩
-
Goss-Sampson, M. A. (2022). Statistical analysis in JASP: A guide for students (5th ed., JASP v0.16.1 2022). https://jasp-stats.org/wp-content/uploads/2022/04/Statistical-Analysis-in-JASP-A-Students-Guide-v16.pdf licensed under CC BY 4.0 Read Descriptive Statistics (pp. 14- pp. 27) Read ANOVA (pp. 91- pp. 98) ↩
-
Çetinkaya-Rundel, M. (2018a, February 20). 5 4 Power calculations for difference of two means [Video]. YouTube. https://youtu.be/vnjjhQDedvs ↩
-
Çetinkaya-Rundel, M. (2018b, February 20). 5 5A ANOVA introduction [Video]. YouTube. https://youtu.be/W36DMVJ4Ibo ↩
-
Çetinkaya-Rundel, M. (2018c, February 20). 5 5B Conditions for ANOVA [Video]. YouTube. https://youtu.be/HGFiWMA5OC8 ↩
-
HeadlessProfessor. (2016, November 12). JASP ANOVA [Video]. YouTube. https://youtu.be/nlAhWQmG5Iw ↩