WA4. Constraint Satisfaction Problem (CSP) Algorithm

Statement

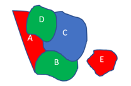
Image 1: Map of a country with 5 districts	Image 2: Graph representation of Fig 1 map

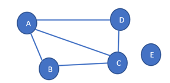Consider the famous map coloring problem. Your goal is to find the minimum number of colors and the color name for the entire map such that two adjacent regions of the map are not colored with the same color. For example, in Fig 1, we need a minimum of 3 colors (red, green, blue).

For this programming assignment, you need to write a program in Java or Python using the Constraint Satisfaction Problem (CSP) algorithm. Here are the detailed requirements.

1. Your program must be complete, compile able, and produce output.
2. Your program must be generic enough to solve problems with other country maps.
3. Your program should be able to handle a minimum of 2 and a maximum of 20 vertices/districts. 2 =< V >= 20, where V is total number of vertices.
4. The total number of colors you can use is 7. Red, Green, Blue, Yellow, Violet, Gray, Orange. Remember, your goal is to choose the minimum number of colors. For example, given in Fig 1, you only need 3 colors to satisfy the goal (no adjacent regions has the same color)
5. Your program will read the graph from a text file (example: graph.txt)
6. Follow the order of the color mentioned in number 4. For example, if you need 4^th color, pick Yellow, if you need 5^th color, then pick Violet and so on. This would be easier for you when you are assessing your peer’s assignment by comparing it with your output.
7. You must follow the CSP backtracking algorithm.
8. If your program can’t solve the problem using 7 colors, it should output “Not Possible with 7 colors.”

Sample Input (graph.txt) (Based on Fig 1):

5
A B C D
B A C
C A B D
D A C
E

• The first line represents the total number of vertices/nodes/districts. In this case, the total number is 5.
• After that, there will be the same number of lines representing the vertex name and their adjacent vertices. Each vertex and it’s adjacent must be separated by space. For example, A B C D means vertex A has 3 adjacent vertices which are B, C, and D. The last line represents the vertex E with no adjacent.

Sample Output:

A red
B green
C blue
D green
E red

• Your output should mention each vertex name in a separate line and the appropriate color name separated by one space.
• If a given map is not possible to color with the given 7 colors, simple output the following line: Not possible with 7 colors

You will be graded on the following:

1. Does the program compile?
2. Does the program correctly read the input file?
3. Does the data structure correctly represent the map/graph?
4. Is the Constraint Satisfaction Problem (CSP) backtracking algorithm correctly implemented?
5. Does the program produce the correct output?
6. Do you think given a scenario where 7 colors are not enough to solve the problem, the program will give the corresponding output?

---

Table of Contents

• WA4. Constraint Satisfaction Problem (CSP) Algorithm
• Statement
• Table of Contents
• Introduction
• Source Code
• Explanation of the Code
• Example Output
  • Input 1: The graph from the statement
  • Input 2: Not possible with 7 colors
  • Input 3: A graph that uses 7 colors
  • Input 4: Two isolated vertices
  • Input 5: Two connected vertices
• Conclusion

---

Introduction

The Constraint Satisfaction Problem (CSP) is a problem-solving technique that deals with a set of variables, each with a domain of possible values, and a set of constraints that specify allowable combinations of values for subsets of variables. The goal is to assign values to the variables in such a way that the constraints are satisfied.

This assignment provides a source code in java, an explanation of the source code, and example outputs for different input files. To run the code, you need to have the inputs folder with some files in it. All files should be passed with the zip folder.

To run the code, you need to:

1. Extract the zip file into a folder.
2. Compile the java code using the command javac Assignment4.java.
3. Run the compiled code using the command java Assignment4.

---

Source Code

Below is the source code for the assignment, all in one file, to make easy to run and test. The main class is Assignment4 which reads the input files from the inputs directory and writes the output files to the outputs directory.

import java.io.IOException;
import java.nio.file.*;
import java.util.*;
import java.util.AbstractMap.SimpleEntry;

enum GraphType {
    DIRECTED,
    UNDIRECTED;

    public static GraphType fromString(String s) {
        if ("directed".equalsIgnoreCase(s)) {
            return DIRECTED;
        } else if ("undirected".equalsIgnoreCase(s)) {
            return UNDIRECTED;
        }
        throw new IllegalArgumentException("Invalid GraphType: " + s);
    }
}

class Edge {

    public String v;
    public String w;

    public Edge(String v, String w) {
        this.v = v;
        this.w = w;
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (!(o instanceof Edge)) return false;
        Edge edge = (Edge) o;
        return Objects.equals(v, edge.v) && Objects.equals(w, edge.w);
    }

    @Override
    public int hashCode() {
        return Objects.hash(v, w);
    }

    @Override
    public String toString() {
        return "[" + v + ", " + w + "]";
    }
}

class Graph {

    private int noOfVertices;
    private int noOfEdges;
    private Map<String, List<String>> adjList;
    private Map<String, Integer> heuristicsCosts;
    private Map<String, Integer> edgeCosts;
    private GraphType graphType;
    private Map<String, Map<String, Object>> metadata;

    public Graph(GraphType type) {
        this.noOfVertices = 0;
        this.noOfEdges = 0;
        this.adjList = new HashMap<>();
        this.heuristicsCosts = new HashMap<>();
        this.edgeCosts = new HashMap<>();
        this.graphType = type;
        this.metadata = new HashMap<>();
    }

    public void addVertex(String v, int heuristicCost) {
        heuristicsCosts.put(v, heuristicCost);
        adjList.put(v, new ArrayList<>());
        noOfVertices++;
        metadata.put(v, new HashMap<>());
    }

    public void addToAdjList(String v, String w) {
        if (!adjList.containsKey(v)) {
            adjList.put(v, new ArrayList<>());
        }
        if (!adjList.get(v).contains(w)) {
            adjList.get(v).add(w);
        }
        if (graphType == GraphType.UNDIRECTED) {
            if (!adjList.containsKey(w)) {
                adjList.put(w, new ArrayList<>());
            }
            if (!adjList.get(w).contains(v)) {
                adjList.get(w).add(v);
            }
        }
    }

    public void addEdge(String v, String w, int cost) {
        addToAdjList(v, w);
        noOfEdges++;
        edgeCosts.put(v + "," + w, cost);
        if (graphType == GraphType.UNDIRECTED) {
            edgeCosts.put(w + "," + v, cost);
        }
    }

    public Set<String> getVertices() {
        return adjList.keySet();
    }

    public Set<Edge> getEdges() {
        Set<Edge> edges = new HashSet<>();
        for (String v : adjList.keySet()) {
            for (String w : adjList.get(v)) {
                edges.add(new Edge(v, w));
            }
        }
        return edges;
    }

    public int getVerticesCount() {
        return noOfVertices;
    }

    public int getEdgesCount() {
        return noOfEdges;
    }

    public Map<String, List<String>> getAdjList() {
        return adjList;
    }

    public int getDegree(String v) {
        List<String> list = adjList.get(v);
        return list == null ? 0 : list.size();
    }

    public List<String> getAdjVertices(String v) {
        return adjList.getOrDefault(v, new ArrayList<>());
    }

    public int getHeuristicCost(String v) {
        Integer cost = heuristicsCosts.get(v);
        return cost == null ? 0 : cost;
    }

    public int getEdgeCost(String v, String w) {
        Integer cost = edgeCosts.get(v + "," + w);
        return cost == null ? 0 : cost;
    }

    public int getCost(String v, String w) {
        return getHeuristicCost(w) + getEdgeCost(v, w);
    }

    @Override
    public String toString() {
        StringBuilder s = new StringBuilder();
        for (String v : adjList.keySet()) {
            s.append(v).append(": ");
            for (String w : adjList.get(v)) {
                s.append(w).append(" ");
            }
            s.append("\n");
        }
        return s.toString();
    }

    public void dfs(String v, Set<String> visited) {
        visited.add(v);
        for (String w : getAdjVertices(v)) {
            if (!visited.contains(w)) {
                dfs(w, visited);
            }
        }
    }

    public void bfs(String v, Set<String> visited) {
        Queue<String> queue = new LinkedList<>();
        queue.add(v);
        visited.add(v);
        while (!queue.isEmpty()) {
            String current = queue.poll();
            for (String w : getAdjVertices(current)) {
                if (!visited.contains(w)) {
                    visited.add(w);
                    queue.add(w);
                }
            }
        }
    }

    public boolean isConnected() {
        for (String v : getVertices()) {
            Set<String> visited = new HashSet<>();
            dfs(v, visited);
            if (visited.size() < noOfVertices) {
                return false;
            }
        }
        return true;
    }

    public Map<String, Object> getGraphProperties() {
        Map<String, Object> properties = new HashMap<>();
        properties.put("type", graphType);
        properties.put("noOfVertices", noOfVertices);
        properties.put("noOfEdges", noOfEdges);
        properties.put("connected", isConnected());
        return properties;
    }

    public void setMetadataKey(String v, String key, Object value) {
        if (metadata.containsKey(v)) {
            metadata.get(v).put(key, value);
        }
    }

    public Object getMetadataKey(String v, String key) {
        if (metadata.containsKey(v)) {
            return metadata.get(v).get(key);
        }
        return null;
    }

    public Map<String, Object> getMetadata(String v) {
        return metadata.get(v);
    }

    public void setMetadata(String v, Map<String, Object> data) {
        metadata.put(v, data);
    }

    public boolean checkAllNodesVisited(List<String> path) {
        if (path.size() != getVerticesCount()) {
            return false;
        }
        for (String v : getVertices()) {
            if (!path.contains(v)) {
                return false;
            }
        }
        return true;
    }

    public Graph copy() {
        Graph newGraph = new Graph(this.graphType);
        for (String v : getVertices()) {
            newGraph.addVertex(v, getHeuristicCost(v));
        }
        for (String v : getVertices()) {
            for (String w : getAdjVertices(v)) {
                newGraph.addEdge(v, w, getEdgeCost(v, w));
            }
        }
        return newGraph;
    }
}

public class Assignment4 {

    // Constant for available colors
    public static final String[] POSSIBLE_COLORS = { "red", "green", "blue", "yellow", "violet", "gray", "orange" };

    public static Graph convertInputToGraph(String input) throws Exception {
        String[] lines = input.trim().split("\\r?\\n");
        int noOfVertices = Integer.parseInt(lines[0].trim());
        Graph graph = new Graph(GraphType.UNDIRECTED);

        if (noOfVertices != lines.length - 1) {
            throw new Exception("Invalid input. Number of vertices does not match the input.");
        }

        if (noOfVertices < 2 || noOfVertices > 20) {
            throw new Exception("Invalid number of vertices. Allowed range: 2-20");
        }

        // Add all vertices first
        for (int i = 1; i <= noOfVertices; i++) {
            String[] tokens = lines[i].split(" ");
            String vertex = tokens[0];
            graph.addVertex(vertex, 0);
        }

        // Add all edges between vertices
        for (int i = 1; i <= noOfVertices; i++) {
            String[] tokens = lines[i].split(" ");
            String vertex = tokens[0];
            for (int j = 1; j < tokens.length; j++) {
                graph.addEdge(vertex, tokens[j], 0);
            }
        }
        return graph;
    }

    public static String chooseColor(Graph graph, String vertex) throws Exception {
        List<String> adjVertices = graph.getAdjVertices(vertex);
        List<String> usedColors = new ArrayList<>();
        for (String v : adjVertices) {
            Object colorObj = graph.getMetadataKey(v, "color");
            if (colorObj != null) {
                usedColors.add(colorObj.toString());
            }
        }
        if (usedColors.size() == POSSIBLE_COLORS.length) {
            throw new Exception("Not possible with 7 colors.");
        }
        for (String color : POSSIBLE_COLORS) {
            if (!usedColors.contains(color)) {
                return color;
            }
        }
        return null;
    }

    public static void colorVertices(Graph graph) throws Exception {
        for (String vertex : graph.getVertices()) {
            String color = chooseColor(graph, vertex);
            graph.setMetadataKey(vertex, "color", color);
        }
    }

    public static List<String> getVerticesColor(Graph graph) {
        List<String> lines = new ArrayList<>();
        for (String vertex : graph.getVertices()) {
            Object color = graph.getMetadataKey(vertex, "color");
            lines.add(vertex + " " + (color != null ? color.toString() : ""));
        }
        return lines;
    }

    public static String convertToMkDown(Graph graph) {
        StringBuilder sb = new StringBuilder();
        sb.append("# Graph\n\n");
        sb.append("```mermaid\n");
        sb.append("graph TD;\n\n");

        for (String v : graph.getAdjList().keySet()) {
            sb.append(v).append("\n");
        }

        sb.append("\n\n");

        for (String v : graph.getAdjList().keySet()) {
            for (String w : graph.getAdjList().get(v)) {
                sb.append(v).append(" --> ").append(w).append("\n");
            }
        }

        sb.append("\n\n");

        String[] colorsDef = {
            "classDef red fill:#FF0000,stroke:#000,color:#fff;",
            "classDef green fill:#008000,stroke:#000,color:#fff;",
            "classDef blue fill:#0000FF,stroke:#fff,color:#fff;",
            "classDef yellow fill:#FFFF00,stroke:#000,color:#000;",
            "classDef violet fill:#8A2BE2,stroke:#000,color:#fff;",
            "classDef gray fill:#808080,stroke:#000,color:#fff;",
            "classDef orange fill:#FFA500,stroke:#000,color:#fff;",
        };

        for (String def : colorsDef) {
            sb.append(def).append("\n");
        }

        List<String> colors = getVerticesColor(graph);
        for (String line : colors) {
            String[] parts = line.split(" ");
            if (parts.length >= 2) {
                String vertex = parts[0];
                String colorName = parts[1];
                sb.append("class ").append(vertex).append(" ").append(colorName).append("\n");
            }
        }

        sb.append("```");
        return sb.toString();
    }

    public static void main(String[] args) {
        try {
            Path inputFolderPath = Paths.get("inputs");
            Path outputFolderPath = Paths.get("outputs");

            // Get list of input files
            List<Path> inputFiles = new ArrayList<>();
            try (DirectoryStream<Path> stream = Files.newDirectoryStream(inputFolderPath)) {
                for (Path entry : stream) {
                    inputFiles.add(entry);
                }
            }
            System.out.println("🟦 Input files: " + inputFiles);

            for (int i = 0; i < inputFiles.size(); i++) {
                Path inputFilePath = inputFiles.get(i);
                String fileName = inputFilePath.getFileName().toString();
                Path outDir = outputFolderPath.resolve(Integer.toString(i));
                if (!Files.exists(outDir)) {
                    Files.createDirectories(outDir);
                }
                Path outputFilePath = outDir.resolve("output" + i + ".txt");
                Path outputMdFilePath = outDir.resolve("graph" + i + ".md");

                try {
                    System.out.println("\n\n\n\n\n\n🟦 Processing file: " + fileName);
                    String inputFile = new String(Files.readAllBytes(inputFilePath));
                    System.out.println("🟪 Read file input:\n" + inputFile + "\n");

                    Graph graph = convertInputToGraph(inputFile);
                    System.out.println("🟨 Printing graph:\n" + graph.toString());
                    System.out.println("🟦 Printing graph properties:\n" + graph.getGraphProperties() + "\n");

                    colorVertices(graph);
                    System.out.println("✅ Coloring vertices");
                    List<String> report = getVerticesColor(graph);
                    for (String line : report) {
                        System.out.println(line);
                    }

                    System.out.println("🟩 Writing to output.txt");
                    Files.write(outputFilePath, String.join("\n", report).getBytes());

                    System.out.println("🟩 Writing to output.md");
                    String outputMd = convertToMkDown(graph);
                    Files.write(outputMdFilePath, outputMd.getBytes());
                } catch (Exception e) {
                    System.err.println("❌ Error: " + e.getMessage());
                    Files.write(outputFilePath, ("Error: " + e.getMessage()).getBytes());
                }
            }
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}

---

Explanation of the Code

• The main class that holds the solution of the problem is Assignment4, which relies on multiple auxiliary classes to define the graph, edges, and the graph type that are Graph, Edge, and GraphType respectively.
• I will not explain the auxiliary classes as they are self-explanatory.
• The Assignment4 class has the following methods:
  • convertInputToGraph(String input): This method converts the input string to a graph object. It reads the input string line by line and adds vertices and edges to the graph object.
  • chooseColor(Graph graph, String vertex): This method chooses a color for a given vertex based on the colors of its adjacent vertices.
  • colorVertices(Graph graph): This method colors all the vertices of the graph by choosing colors for each vertex.
  • getVerticesColor(Graph graph): This method returns a list of strings containing the vertices and their colors, ready to be printed or written to a file.
  • convertToMkDown(Graph graph): This method converts the graph object to a markdown string that can be used to visualize the graph in a markdown file.
  • main(String[] args): This is the main method, and it does the following:
    • Reads the input files from the inputs directory.
    • Processes each input file by converting it to a graph, coloring the vertices, and writing the output to a file.
    • If an error occurs during processing, it writes the error message to the output file.

---

Example Output

Below are the example outputs for different input files. For each file we will see the input, the standard output, the written file, and a markdown mermaid image that represents the graph with colored vertices.

Input 1: The graph from the statement

This is the input file supplied and solved in the problem statement, which is a map of a country with 5 districts. Here is the input file:

5
A B C D
B A C
C A B D
D A C
E

The output file is:

A red
B green
C blue
D green
E red

Below are the output and the mermaid markdown image:

Image 1-1: Standard output 1

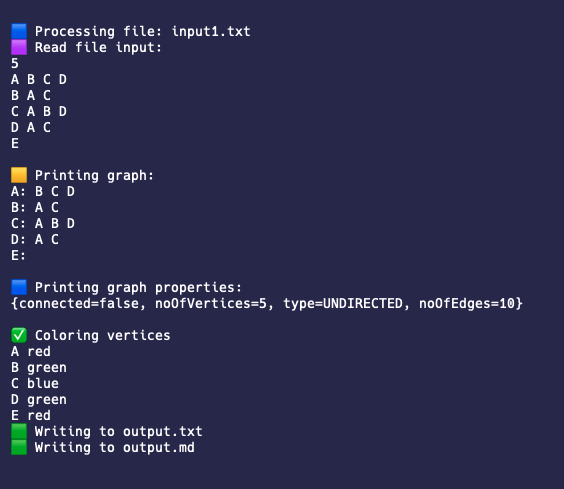Image 1-2: Markdown graph 1

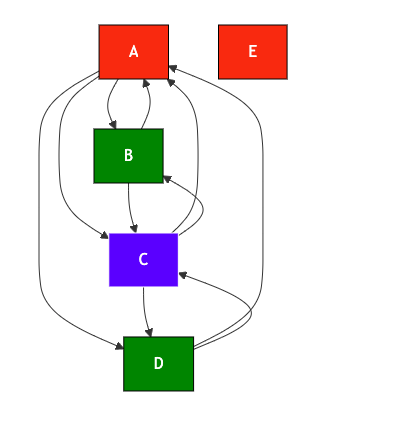Input 2: Not possible with 7 colors

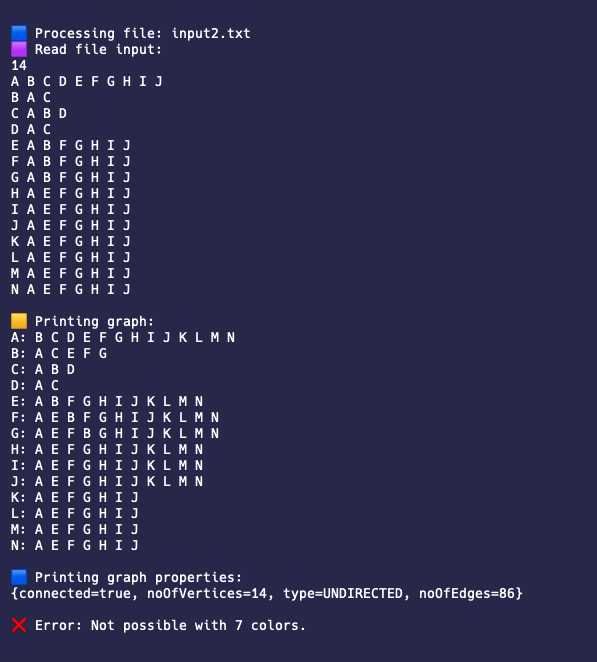
This is an input file where the graph is not possible to color with 7 colors. The input is consisted of 14 deeply connected vertices that make it impossible to color with 7 colors only. Here is the input file:

Here is the input file:

14
A B C D E F G H I J
B A C
C A B D
D A C
E A B F G H I J
F A B F G H I J
G A B F G H I J
H A E F G H I J
I A E F G H I J
J A E F G H I J
K A E F G H I J
L A E F G H I J
M A E F G H I J
N A E F G H I J

The output file is:

Error: Not possible with 7 colors.

The graph is not possible due to the function exiting early, and below are the standard output,

Image 2-1: Standard output 2

Input 3: A graph that uses 7 colors

The following input consists of 10 deeply connected vertices that require all 7 colors to be colored. Here is the input file:

10
A B C D E F G H I J
B A C
C A B D
D A C
E A B F G H I J
F A B F G H I J
G A B F G H I J
H A E F G H I J
I A E F G H I J
J A E F G H I J

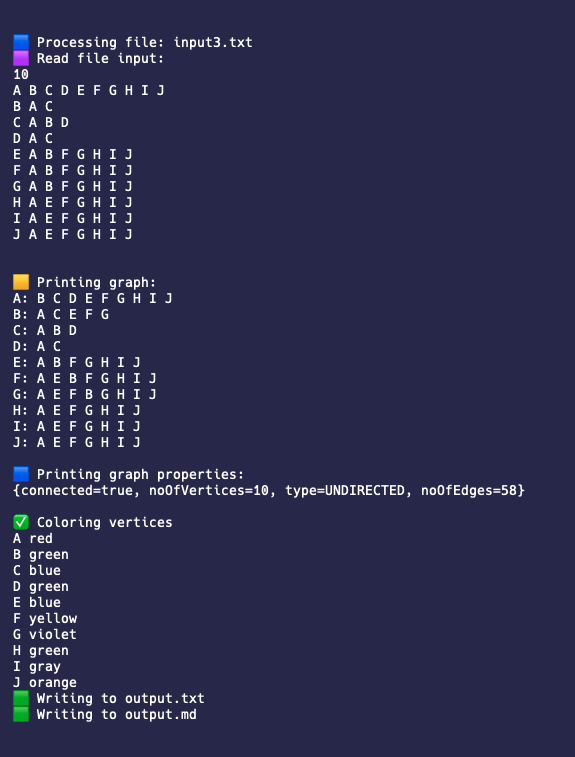
The output file is:

A red
B green
C blue
D green
E blue
F yellow
G violet
H green
I gray
J orange

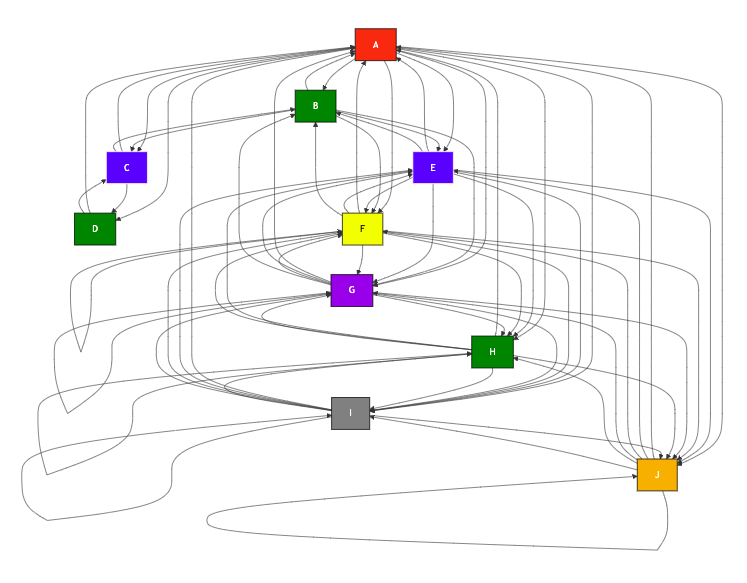
Below are the standard output and the mermaid markdown image:

Image 3-1: Standard output 3

Image 3-2: Markdown graph 3

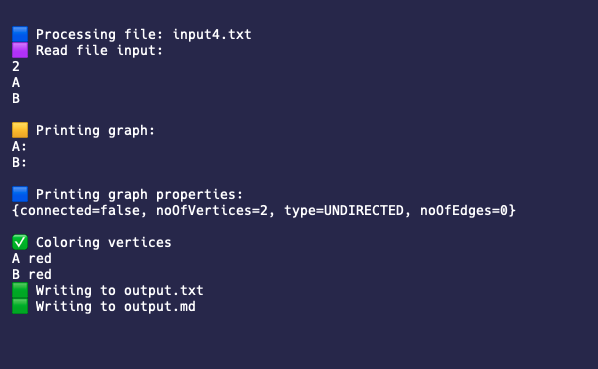
Input 4: Two isolated vertices

This input file consists of two isolated vertices that do not have any edges connecting them; hence they both should be colored red. Here is the input file:

2
A
B

The output file is:

A red
B red

Below are the standard output and the mermaid markdown image:

Image 4-1: Standard output 4

Image 4-2: Markdown graph 4

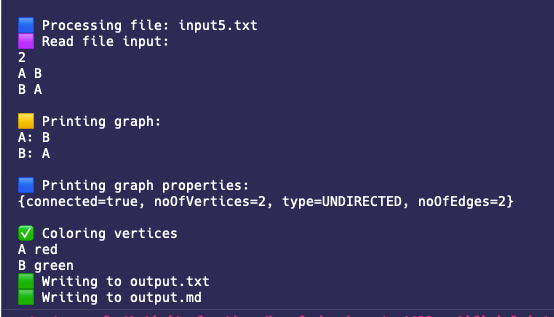
Input 5: Two connected vertices

This input file consists of two connected vertices that are connected with an edge; hence they should get different colors. Here is the input file:

2
A B
B A

The output file is:

A red
B green

Below are the standard output and the mermaid markdown image:

Image 5-1: Standard output 5

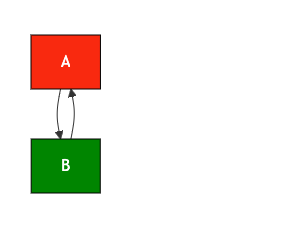
Image 5-2: Markdown graph 5

---

Conclusion

We have provided the source code, source code explanation and various example outputs, and here are our checks for the assignment requirements:

Aspect	Achieved	Comments
Does the program compile?	✅
Does the program correctly read the input file?	✅	Input 1 above.
Does the data structure correctly represent the map/graph?	✅	See the output diagrams.
Is the Constraint Satisfaction Problem (CSP) backtracking algorithm correctly implemented?	✅	Notice the chooseColor methods backtracks to the right color based on the constraints.
Does the program produce the correct output?	✅	See the output for each of the examples above.
Do you think given a scenario where 7 colors are not enough to solve the problem?	✅	See examples 2 and 3 above.