DA6. Quick Sort¶
Statement¶
-
Develop a sorting algorithm. Your sorting algorithm may only be an implementation of the shellsort, mergesort, or quicksort. Your algorithm must use an array of integers of at least 21 different items. The items in the list must be in random order. Your algorithm must sort the list using the sorting algorithm that you have chosen and keep track of the number of exchanges that are required to sort the list. This value along with the contents of the sorted list must be displayed as output to the algorithm to the console.
-
In the preceding code example, you will note that the array to be sorted contains 21 random items, which are sorted by the algorithm, which happens to be an insertion sort. Your assignment will be to create your own sort algorithm that implements one of the following types of sort: shellsort, mergesort, quicksort. Please use the same list of items in your sort that are in the preceding example as follows:
12,9,4,99,120,1,3,10,23,45,75,69,31,88,101,14,29,91,2,0,77 -
As part of your assignment, you must submit both a description of the assignment and how your algorithm works, including an Asymptotic analysis of your algorithm. Your analysis must include the efficiency of your algorithm expressed in Big Oh, Big Omega, or Big Theta notation as appropriate.
-
Please indicate in your description whether your algorithm implements a shellsort, mergesort, or quicksort. This must include a description of how your selected algorithm functions and why it is more efficient than the insertion sort above.
We- will obtain another measure of efficiency by comparing the number of exchanges that were required to complete the sort. For the insertion sort above, the required number of exchanges is 114. You should compare this with the number of exchanges required by your sorting algorithm in your description. Please discuss whether your output was what you expected.
- Further, as part of your assignment, you must include the code of your algorithm. All of these elements of this assignment must be completed and posted to the assignment for Unit 6 by the end of the week for unit 6.
Contents¶
Conclusion¶
- This text will choose the Quick Sort algorithm to sort the array of integers.
- Two java files are include:
- The
Wa6.java: a class that contain modern java code that can be run directly. - The
Wa6Jeliot.java: includes java code that can be run in Jeliot tool.
- The
- Quick Sort is a general-purpose, in-memory, space efficient internal sorting algorithm that uses the divide and conquer strategy (Shaffer, 2011) and it is the fastest known sorting algorithm in practice (Shaffer, 2011).
- Our implementation chooses the middle element in the array as pivot, then partition around it.
Output¶
- The output of running the
Wa6.javafile is as follows: 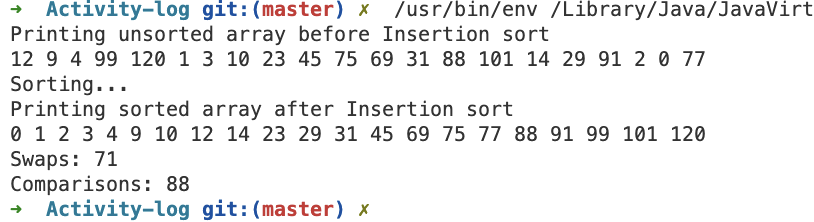
- The output of running the
Wa6Jeliot.javaon the Jeliot tool is as follows: 
Asymptotic Analysis¶
- Worst case: O(n^2), after the first pivot, the partitioning is always unbalanced as zero elements in the left partition and n-1 elements in the right partition (or vice versa).
- Best case: O(n log n), when the pivot is always the median of the partition, so that the number of elements in the left and right partitions are equal.
- Average case: O(n log n) (Shaffer, 2011).
Code¶
public class Wa6 {
static int swaps = 0;
static int comparisons = 0;
public static <E> void swap(E[] array, int index1, int index2) {
E temp = A[index1];
A[index1] = A[index2];
A[index2] = temp;
swaps++;
}
static <E extends Comparable<? super E>> void qSort(E[] A, int i, int j) {
int pivotIndex = findPivot(A, i, j); // pivot is the median of array values (in theory), we are using the middle element here
swap(A, pivotIndex, j); // put pivot at end of array, to be easily restored later
int k = partition(A, i - 1, j, A[j]); // Partition, returns first position in right partition where pivot belongs
swap(A, k, j); // put pivot in kth position
comparisons++;
if ((k - i) > 1) qSort(A, i, k - 1); // Sort left partition
comparisons++;
if ((j - k) > 1) qSort(A, k + 1, j); // Sort right partition
}
static <E extends Comparable<? super E>> int findPivot(E[] A, int i, int j) {
return (i + j) / 2;
}
static <E extends Comparable<? super E>> int partition(E[] A, int l, int r, E pivot) {
do {
while (A[++l].compareTo(pivot) < 0) {
// as long as A[l] < pivot, keep moving right
comparisons++;
}
while ((r != 0) && (A[--r].compareTo(pivot) > 0)) {
// as long as A[r] > pivot, keep moving left
comparisons++;
}
swap(A, l, r); // swap elements so they end up in the correct partition
} while (l < r); // continue, until the two pointers meet
swap(A, l, r); // Reverse last, wasted swap because of the extra loop iteration
return l; // Return first position in right partition (the new pivot's position)
}
public static void main(String[] args) {
Integer[] arr1 = { 12, 9, 4, 99, 120, 1, 3, 10, 23, 45, 75, 69, 31, 88, 101, 14, 29, 91, 2, 0, 77 }; /// 21 elements
System.out.println("Printing unsorted array before Insertion sort");
for (int i : arr1) System.out.print(i + " ");
System.out.println();
System.out.println("Sorting...");
qSort(arr1, 0, arr1.length - 1);
System.out.println("Printing sorted array after Insertion sort");
for (int i : arr1) System.out.print(i + " ");
System.out.println();
System.out.println("Swaps: " + swaps);
System.out.println("Comparisons: " + comparisons);
}
}
References¶
- Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf. Chapter 7: Internal Sorting.