Skip to content

JA7- Absenteeism in School (Multiple Regression Example)

Statement

A study was conducted on absenteeism in school and the data was procured. Use the collected data to answer the following questions (Data: absenteeism.csv).

  • a. Import the dataset in JASP and run the regression where days is the dependent variable and the explanatory variables (factors) are:- eth (0- aboriginal, 1- not aboriginal), sex (0- female, 1- male) and lnr (0 – average learner, 1- slow learner). Show the full output from JASP.
  • b. Write the equation of the regression model
  • c. Interpret each one of the slopes in this context. Determine if each of the slopes are statistically significant based on the p-value for an alpha significance of 5%.
  • d. Calculate the residual for the second observation in the data set.
  • e. What is the model adjusted R-squared value? Interpret it.

Answer

Regression Analysis Process Using JASP

Here is a step by step guide to the analysis performed in JASP, following the guide by Research By Design (2020):

  • Convert the data to a CSV file:
    • The data is provided as a xlsx file, which is not directly compatible with JASP. We need to convert it to a csv file.
    • I opened the file in Excel and saved it as a csv file named absenteeism.csv.
  • Load the data into JASP:
    • Use File > Open from the top menu.
    • Select Computer and then Browse.
    • Select the dataset file.
  • Configure the fields:
    • The dataset has the following fields days, eth, sex, age, and lnr.
    • The eth, lnr, and sex variables are categorical, and not numerical; we need to associate a number to each category.
    • Fix the eth (ethnicity) variable:
      • The eth variable has two categories: aboriginal (A) and not aboriginal (N).
      • Aboriginal = A = 0.
      • Not Aboriginal = N = 1.
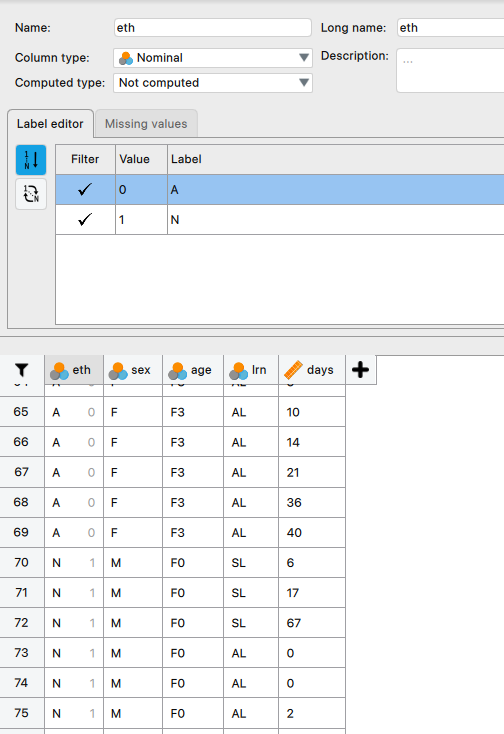
      • Double click on the eth column name to open the Variable Properties.
      • Select Nominal under Variable Role.
      • Update the Values to 0 = A, 1 = N, according to Image 1 below.
    • Fix the sex variable:
      • The sex variable has two categories: female (F) and male (M).
      • Female = F = 0.
      • Male = M = 1.
      • We update the sex variable as we did with the eth variable above.
    • Fix the lnr variable:
      • The lnr variable has two categories: average learner (A) and slow learner (S).
      • Average learner = A = 0.
      • Slow learner = S = 1.
    • Fix the age variable:
      • The age variable has 4 categories: F0, F1, F2, and F3.
      • F0 = 0, F1 = 1, F2 = 2, F3 = 3.
  • Do the Regression analysis:
    • Use Regression > Classical > Linear Regression from the top menu.
    • Dependent variable is the y variable which is days.
    • Covariate is the x variable, which are eth, sex, and lnr (added in order).
    • Set the Method to Enter.
    • Under Statistics:
      • Select Regression Coefficient > Confidence intervals.
      • Select Regression Coefficient > Descriptives.
      • Select Residuals > Statistics to check for outliers and influential points (Std. Residuals should be between -3 and 3).
      • Select Residuals > Durbin-Watson to check for independence of observations (Durbin-Watson statistic should be between 1 - 3).
    • Under Plots:
      • Select Residuals plots > Residuals vs Histogram to check for normality.
      • Select Q-Q plot standardized residuals to check for normality.
      • Select Residuals vs predicted to check for homoscedasticity.
Image 1: Variable Properties for eth
Variable Properties for eth

Results of the Analysis

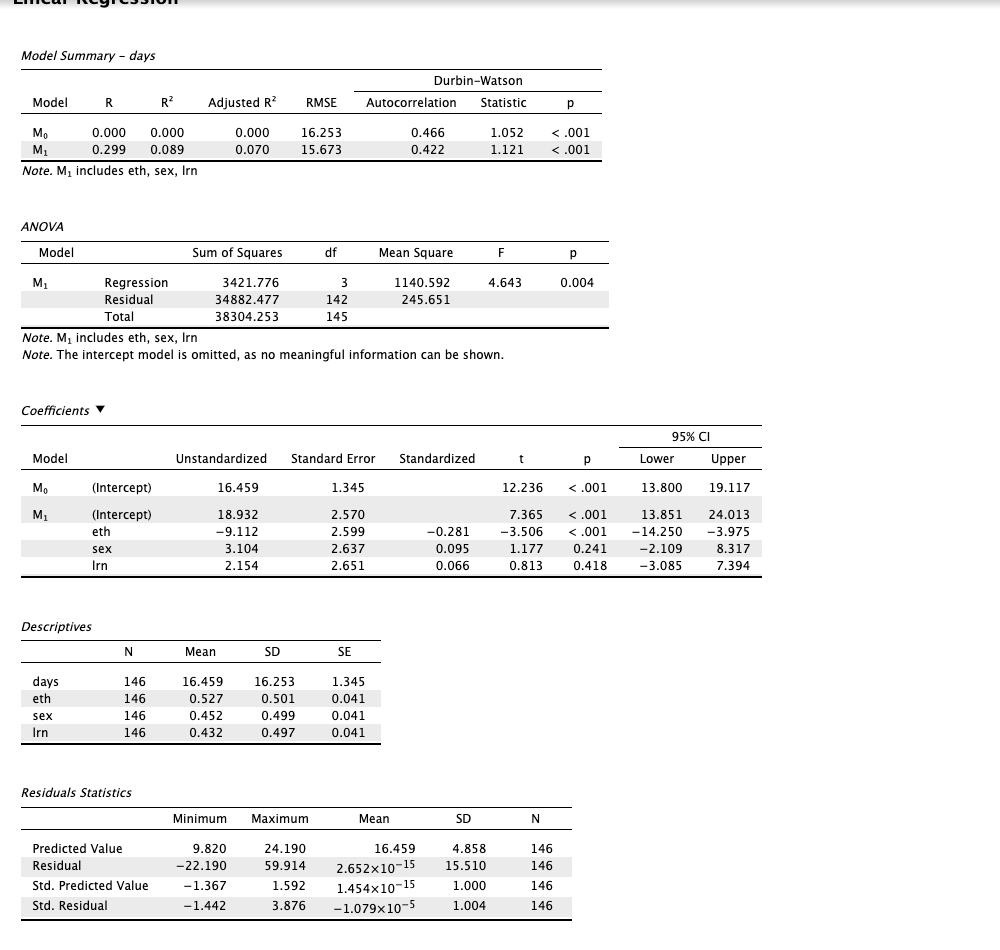
We have loaded the data into JASP and performed the linear regression analysis. The results are as follows:

Image 2: Linear Regression Output
Linear Regression Output
Image 3: Linear Regression Output (2)
Linear Regression Output (2)

A. Import the dataset in JASP and run the regression where days is the dependent variable and the explanatory variables (factors) are:- eth (0- aboriginal, 1- not aboriginal)

The regression analysis was performed in JASP with the dependent variable days and the explanatory variables eth, sex, and lnr. The output is shown in the images (2 and 3) above.

B. Write the equation of the regression model

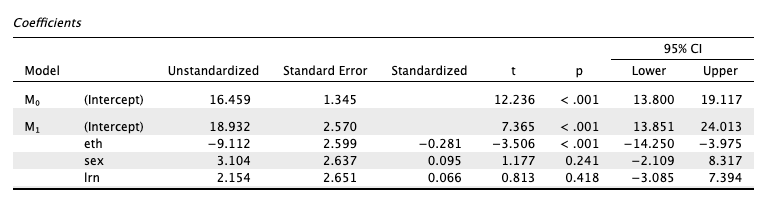
Looking at the coefficients table in the output, shown in the Image 4 below:

Image 4: Coefficients Table
Coefficients Table

The general form of the regression equation is:

\[ \text{days} = \beta_0 + \beta_1 \times \text{eth} + \beta_2 \times \text{sex} + \beta_3 \times \text{lnr} \]

From the table, the coefficients are:

Coefficient Name Value
\(\beta_0\) Intercept 18.932
\(\beta_1\) eth -9.112
\(\beta_2\) sex 3.104
\(\beta_3\) lnr 2.154

Therefore, the regression equation is:

\[ \text{days} = 18.932 - 9.112 \times \text{eth} + 3.104 \times \text{sex} + 2.154 \times \text{lnr} \]

C. Interpret each one of the slopes in this context. Determine if each of the slopes are statistically significant based on the p-value for an alpha significance of 5%

Looking at the coefficients table in the output, shown in the Image 4 below:

Image 4: Coefficients Table
Coefficients Table

From the table, the coefficients are:

Coefficient Name Value P-value Significant Correlation
\(\beta_0\) Intercept 18.932 0.001 Yes -
\(\beta_1\) eth -9.112 0.001 Yes Negative
\(\beta_2\) sex 3.104 0.241 No Positive
\(\beta_3\) lnr 2.154 0.418 No Positive

Here is the interpretation of the slopes:

  • Ethnicity: (1 for not aboriginal, 0 for aboriginal):
    • For every unit increase in the eth variable (from aboriginal to not aboriginal), the number of days absent decreases by 9.112 days due to the negative sign.
    • The slope is statistically significant (p-value = 0.001).
    • Thus, not aboriginal students (higher eth value) tend to have fewer days absent compared to aboriginal students.
    • Specifically, Not Aboriginal students are expected to be absent for 9.112 days less (on average) than Aboriginal.
  • Sex: (1 for male, 0 for females):
    • For every unit increase in the sex (from females to males), the number of days absent increases by 3.104 days due to the positive sign.
    • The slope is not statistically significant (p-value = 0.241).
    • Thus, there is no significant difference in the number of days because we cannot reject the null hypothesis (p-value > 0.05).
    • However, if we would tolerate a higher Type I error rate, the data shows that males tend to be absent for more days (3.104 days on average) than females.
  • Learner Type: (1 for slow learner, 0 for average learner):
    • For every unit increase in the lnr variable (from average to slow learner), the number of days absent increases by 2.154 days due to the positive sign.
    • The slope is not statistically significant (p-value = 0.418).
    • Thus, there is no significant difference in the number of days because we cannot reject the null hypothesis (p-value > 0.05).
    • However, if we would tolerate a higher Type I error rate (very unlikely), the data shows that slow learners tend to be absent for more days (2.154 days on average) than average learners.

D. Calculate the residual for the second observation in the data set

The residuals are the differences between the observed values and the predicted values. The second observation in the dataset is (O2)

Ethnicity Sex Age Learner Type Days
A=0 M=1 F0=0 SL=1 11

Let’s compute the days for the scend observation (O2) using the regression equation:

\[ \begin{aligned} \text{days} &= 18.932 - 9.112 \times \text{eth} + 3.104 \times \text{sex} + 2.154 \times \text{lnr} \\ &= 18.932 - 9.112 \times 0 + 3.104 \times 1 + 2.154 \times 1 \\ &= 18.932 + 3.104 + 2.154 \\ &= 24.19 \end{aligned} \]

The residual for the second observation is:

\[ \begin{aligned} \text{Residual} &= \text{Observed Value} - \text{Predicted Value} \\ &= 11 - 24.19 \\ &= -13.19 \end{aligned} \]

Thus, the residual for the second observation is -13.19.

E. What is the model adjusted R-squared value? Interpret it

Image 6: Model Summary
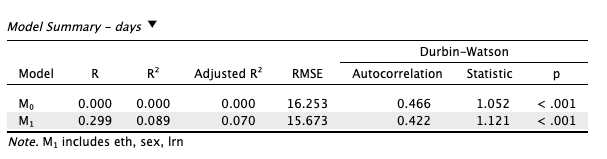Model Summary

The adjusted R-squared value is a measure of how well the independent variables explain the variance in the dependent variable. It adjusts the R-squared value for the number of predictors in the model and the degrees of freedom.

The R^2=0.089 and the Adjusted R^2=0.070 in the according to the image above. We will interpret the adjusted R-squared value as is more reliable when there are multiple predictors in the model.

Here are some notes about the interpretation:

  • Only 8% of the variance in the dependent variable days is explained by the independent variables eth, sex, and lnr.
  • There is a 1% difference between the R-squared and the adjusted R-squared values, which indicates that adding the predictors did not significantly improve the model.
  • The low adjusted R-squared value suggests that the entire model is questionable as it does not explain much of the variance in the dependent variable.
  • Maybe trying to add/remove one or more predictors will yield a better Adjusted R-squared value, hence, a better model.

References