4. Binary Trees¶

Introduction¶

\S**[^.\s:,]
Trees Terminology³ ¹:
- Root: The topmost node of a tree.
- Parent: A node that has a child node. also known as Ancestor.
- Child: A node that has a parent node. also known as Descendant.
- Sibling: Nodes that have the same parent.
- Subtree: A tree that is part of another tree.
- Leaf: A node that has two empty children.
- Internal Node: A node that has at least one non-empty child.
- Path to a node: A sequence of nodes that link to a particular node starting from the root.
- Depth of a node: The number of edges from the root to the node, aka. the number of levels between the node and the root, ak, length of the path from the root to the node. (the root has a depth of 0).
- Level of a node: The depth of a node, all nodes at the same depth are at the same level. (the root has a level of 0).
- Height of the tree: The number of edges on the longest path from a node to a leaf, aka. the number of levels in the tree, or the**Depth of the deepest node in the tree +1**.
- Unbalanced Tree: A tree that has a height that is much larger than the minimum possible height. aka, the Height of the left subtree is much larger than the Height of the right subtree, or vice versa.
- Approaches to balancing a trees: AVL, 2-3-4, Red-Black
- Rotation: transforming (restructuring) a tree to maintain its balance.
- Traversal: Visiting all nodes in a tree.
  - Pre-Oder: Visit the root node first, then recursively visit the left subtree, then recursively visit the right subtree.
  - Post-Order: Recursively visit the left subtree, then recursively visit the right subtree, then visit the root node.
  - In-Order: Recursively visit the left subtree, then visit the root node, then recursively visit the right subtree.
  - Breadth-First: Visit all nodes at a given level before visiting any nodes at the next level.
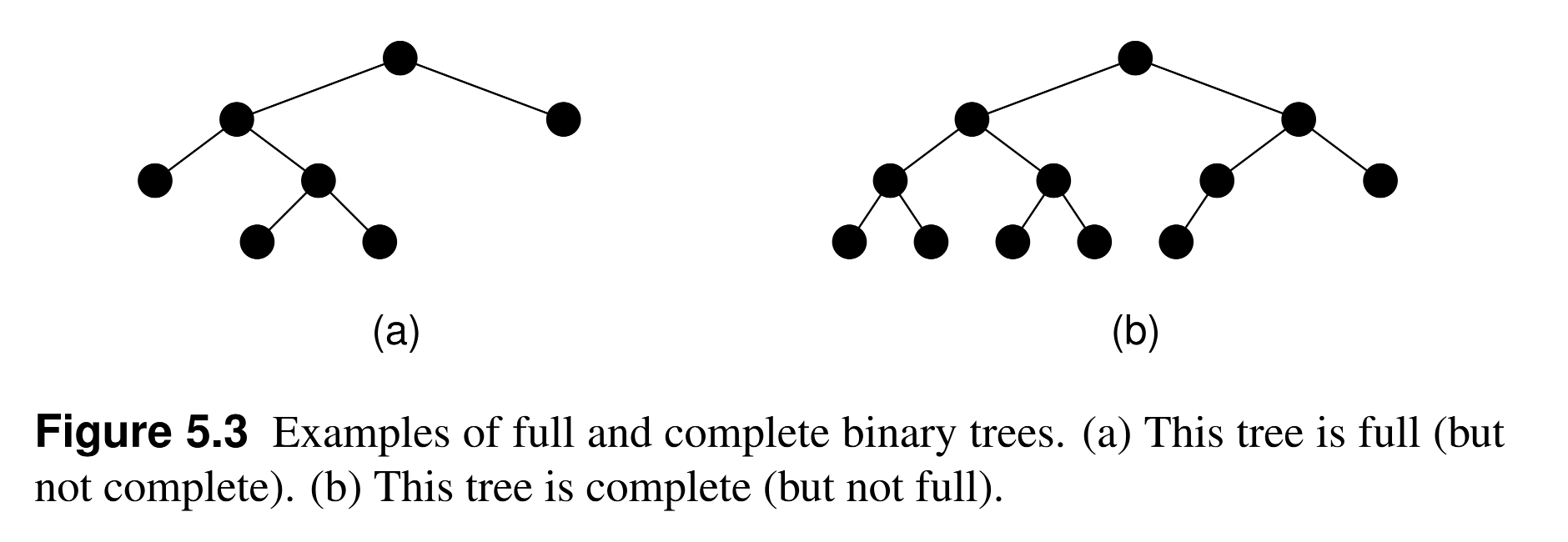
Full Binary Tree:
- A tree in which every node has either 0 or 2 children, but never 1 child.
- Example: The Huffman Coding Tree.
Complete Binary Tree:
- A tree in which every level, except possibly the last and last -1, is completely filled (has two children).
- All leaves are at the last or last-1 levels, and no leaves before that level
- Complete trees start filling nodes from left to right, so that all nodes are as far left as possible.
- Example: Heap.

Binary Search Tree (BST) ²¶

It is a tree that has the following properties (for any noden, including the root node):
- Has at most two children.
- The left child is less than the parent.
- The right child is greater than the parent.
All operations (insertion, lookup -search-, delete) on BST are inO(log n) if the tree is reasonably balanced.
Insert(int value). steps:
1. If the root isnull (aka, the tree is empty), then create a new node and make it the root.
2. Ifvalue is less than the root, then insert it in the left subtree recursively (aka, call the insert method on the left subtree).
3. Ifvalue is greater than the root, then insert it in the right subtree recursively (aka, call the insert method on the right subtree).
Find (int value) (or lookup, or contains or search), returns true if the node is in the tree or false otherwise. steps:
1. If the root isnull (aka, the tree is empty), then the node is not in the tree (return false).
2. Ifvalue is equal to the root, then the node is in the tree (return true).
3. Ifvalue is less than the root, then search for it in the left subtree recursively (aka, call the search method on the left subtree).
4. Ifvalue is greater than the root, then search for it in the right subtree recursively (aka, call the search method on the right subtree).
FindParent(int value). finds the parent node of a given value.
FindNode(int value). finds the node of a given value and returns its reference.
FindMin(). finds the minimum value in the tree.
- Traverse the tree to the left until you reach a leaf node (aka, the leftmost node).
- For each node, only traverse to the left.
FindMax(). finds the maximum value in the tree
- Traverse the tree to the right until you reach a leaf node (aka, the rightmost node).
- For each node, only traverse to the right.
Delete (int value) is a bit complicated; this removes the first appearance of a node in the tree; it returns true if the node is deleted or false otherwise. steps:
1. Find the node to delete (if it exists) and call itNode
2. Find the parent ofNode and call itParentNode
3. IfNode is not found, then return false.
4. IfNode is the root of the tree and no other nodes in the tree (size or tree count = 1), set the root tonull. (aka, the tree is empty now).
5. IfNode is a leaf (has no children):
  - set the parent’s child tonull.
  - IfNode is left to its parent (aka.Node <ParentNode), then setParentNode.left tonull.
  - IfNode is right to its parent (aka.Node >ParentNode), then setParentNode.right tonull.
6. IfNode has only one left child (left subtree),
7. IfNode has only one right child (right subtree),
8. IfNode has two children (left and right subtrees),
9. Reduce the size of the tree by one.

Tree Traversal¶

Traversal	Pre-Order	Post-Order	In-Order	Breadth-First
first	root	left	left	root
second	left	right	root	left (current depth only)
third	right	root	right	right (current depth only)
fourth				BreadthFirst(next depth level)

Heap ⁴¶

Heap is a special binary tree that has two strategies:
- Min Heap: the root is the minimum value in the tree, and each node is less than or equal to its children.
- Max Heap: the root is the maximum value in the tree, and each node is greater than or equal to its children.
Mostly implemented as an array rather than a linked list.
Finding indexes in an array based heap

Index	Expression	Description
Parent	`floor((i-1)/2)`	The parent of the node at index `i`
Left	`2i + 1`	The left child of the node at index `i`
Right	`2i + 2`	The right child of the node at index `i`

Heap Operations¶

Insert:
- Insert the new node at the end of the array.O(1)
- Validating the heap order (aka, re-balancing the heap) by swapping necessary nodes.O(log n), usually, we swap the new node with its parent until the heap order is valid.
Delete:
- Find the index of the node to delete.O(n)
- Swap the node with the last node in the array.O(1)
- Validate the heap order (aka, re-balancing the heap) by swapping necessary nodes.O(log n), usually, we swap the new node with its parent until the heap order is valid.
Search:
- Search for the node in the array.O(n)

5. Binary Trees ¹¶

Binary trees allow both insert and search operations inO(log n) time.
Binary trees are useful in prioritizing jobs, describing mathematical expressions, compressing algorithms, and syntactic functions of programming languages (e.g., syntax trees).

5.1.1 The Full Binary Tree Theorem¶

Leaves vs internal nodes:
- Some binary Tree implementations stores data only in the leaves and uses the internal nodes for structural purposes only.
- In this case, space requirement for leaves is different than internal nodes (usually, leaves are more than internal nodes).
- To know space requirement for these binary trees, the fraction of leaves/total nodes and internal nodes/total nodes must be known.
- These fractions are not fixed.
Theorem 5.1. Full Binary Tree Theorem: The number of leaves in a nonempty full binary tree is one more than the number of internal nodes.
Theorem 5.2: The number of empty subtrees in a nonempty full binary tree is one more than the number of nodes in the tree.

Theorem 5.1: for a full binary tree, numOfLeaves = numOfInternalNodes + 1
Theorem 5.2: for a `any` binary tree, numOfEmptySubtrees = numOfNodes + 1

Binary Trees that use different types for internal nodes and leaves:
- PR Quad Tree.
- Huffman Coding Tree.
- Representing mathematical expressions.

5.1.2 A Binary Tree Node ADT¶

/** ADT for binary tree nodes */
public interface BinNode<E> {
    public E element();
    public void setElement(E v);
    public BinNode<E> left();
    public BinNode<E> right();
    public boolean isLeaf();
}

5.2 Binary Tree Traversals¶

Traversal: any operation that involves visiting all nodes in a tree in some order.
Enumeration any traversal operation that lists every node in the tree precisely once.
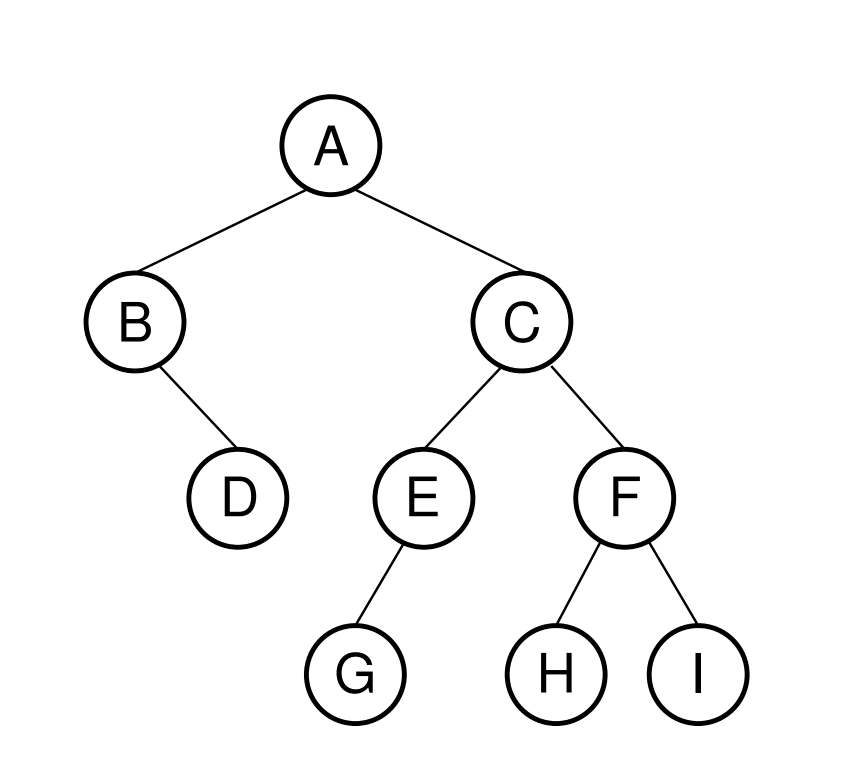
Traversal types (will take above tree as example):
- PreOrder: visit the root, then recursively visit the left then right subtrees.
  - A B D C E G F H I
  - The first node visited is the root, then all nodes in the left subtree, then all nodes in the right subtree.
  - Use case: printing tree while preserving the structure and relationships between nodes.
- PostOrder: recursively visit the left subtree, then the right subtree, then the root.
  - D B G E H I F C A
  - The last element printed is the root of the tree.
  - Deleting a subtree, where the children of a node must be deleted before the node itself.
- InOrder: visit all nodes in the left subtree, then the root, then all nodes in the right subtree.
  - B D A G E C H F I
  - The root is visited between the left and right subtrees.
  - Use case: printing a tree in sorted order.

5.3 Binary Tree Node Implementations¶

Linked Binary Tree Node:

/**
 * Binary tree node implementation: Pointers to children
 * @param E The data element
 * @param Key The associated key for the record
 */
class BSTNode<Key, E> implements BinNode<E> {
    private Key key; // Key for this node
    private E element; // Element for this node
    private BSTNode<Key,E> left; // Pointer to left child
    private BSTNode<Key,E> right; // Pointer to right child

    /** Constructors */
    public BSTNode() {left = right = null; }
    public BSTNode(Key k, E val){ left = right = null; key = k; element = val; }
    public BSTNode(Key k, E val,  BSTNode<Key,E> l, BSTNode<Key,E> r){
        left = l; right = r; key = k; element = val;
    }

    /** Get and set the key value */
    public Key key() { return key; }
    public void setKey(Key k) { key = k; }

    /** Get and set the element value */
    public E element() { return element; }
    public void setElement(E v) { element = v; }

    /** Get and set the left child */
    public BSTNode<Key,E> left() { return left; }
    public void setLeft(BSTNode<Key,E> p) { left = p; }

    /** Get and set the right child */
    public BSTNode<Key,E> right() { return right; }
    public void setRight(BSTNode<Key,E> p) { right = p; }

    public boolean isLeaf() { return (left == null) && (right == null); }
}

Notes about the above implementation:
- No need for a parent pointer, since we can use recursion to find the parent.
- If you need to store parent pointer, there is a chance that a better implementation is needed or that you do not know recursion.
- It uses the same type for Laves and Internal Nodes.

Mathematical Expressions as Binary Trees¶

Internal nodes are operators, leaves are operands.
Example4x (2x + a) - c represented in the image below: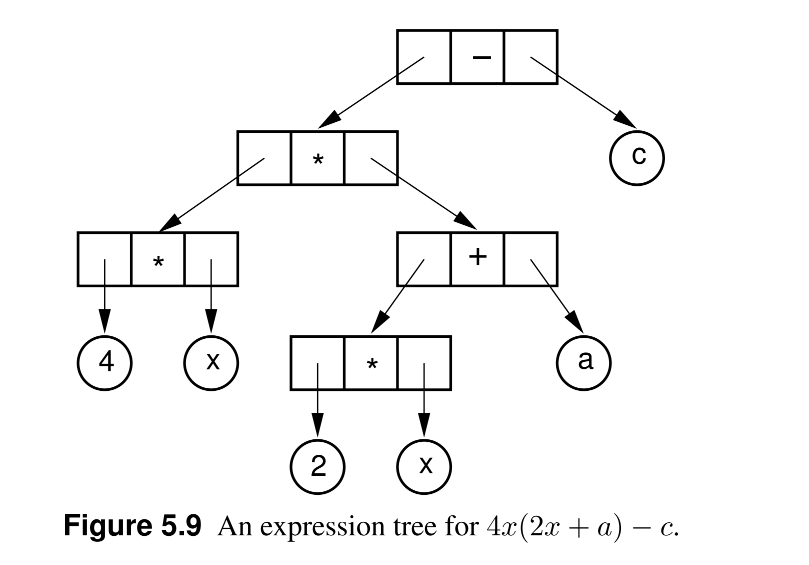
It is an example of different types for leaves and internal nodes:
- Internal Nodes: Operators, small fixed size, do include pointers to children.
- Nodes: Operands, large variable size, do NOT include pointers to children.

/** Base class for expression tree nodes */
public interface VarBinNode {
    public boolean isLeaf(); // All subclasses must implement
}

/** Leaf node */
class VarLeafNode implements VarBinNode {
    private String operand; // Operand value

    public VarLeafNode(String val) {
        operand = val;
    }

    public boolean isLeaf() {
        return true;
    }

    public String value() {
        return operand;
    }
};

/** Internal node */
class VarIntlNode implements VarBinNode {
    private VarBinNode left; // Left child
    private VarBinNode right; // Right child
    private Character operator; // Operator value

    public VarIntlNode(Character op, VarBinNode l, VarBinNode r) {
        operator = op;
        left = l;
        right = r;
    }

    public boolean isLeaf() {
        return false;
    }

    public VarBinNode leftchild() {
        return left;
    }

    public VarBinNode rightchild() {
        return right;
    }

    public Character value() {
        return operator;
    }

    /** Preorder traversal */
    public static void traverse(VarBinNode rt) {
        if (rt == null) return; // Nothing to visit
        if (rt.isLeaf()) { // Process leaf node
            Visit.VisitLeafNode(((VarLeafNode) rt).value());
        } else { // Process internal node
            Visit.VisitInternalNode(((VarIntlNode) rt).value());
            traverse(((VarIntlNode) rt).leftchild());
            traverse(((VarIntlNode) rt).rightchild());
        }
    }
}

Using the Composite Pattern to implement the above makes the interfaceVarBinNode declares bothisLeaf() andtraverse() methods and the classesVarLeafNode andVarIntlNode implement them accordingly.

/** Base class: Composite */
public interface VarBinNode {
    public boolean isLeaf();
    public void traverse();
}

Space Requirements for Binary Trees¶

Definitions in the below examples:
- P the space required to store a single pointer.
- D the space required to store a single data element.
- n the number of nodes in the tree.
- Space Overhead the space required to store the tree structure.
- Total Space the space required to store the tree structure and the data elements = Space Overhead + Data Space.

Implementation	Space Overhead	Data Space	Total Space	Overhead fraction	Comments
Simple Tree (internal and leaves of the same type)	n* 2P	n* D	n* (2P + D)	2P / (2P + D)	If P=D, ⅔ of the space is overhead. Accoring to 5.2 theorem, numOfLeaves = nomOfInteralNodes + 1, have empty pointers (wasted). Internal nodes that do not hold data have their data pointers wasted. In total, half of pointers in the tree are wasted.
Simple Tree (store pointers to data)	n* 3P (2 pointers to childern, 1 pointer to data)	n* D (note: data stored outside of the tree)	n* 3P	3P / (3P + D)
Different types for Leaves and Internal nodes	½n * (2P) (all leaves’ pointers are empty = half of n)	n * D	½n (2P) + nD	P / (P + D)	If tree is not full, overhead is higher. Overhead percentage drops as tree get closer to full.

5.3.3 Array Implementation for Complete Binary Trees¶

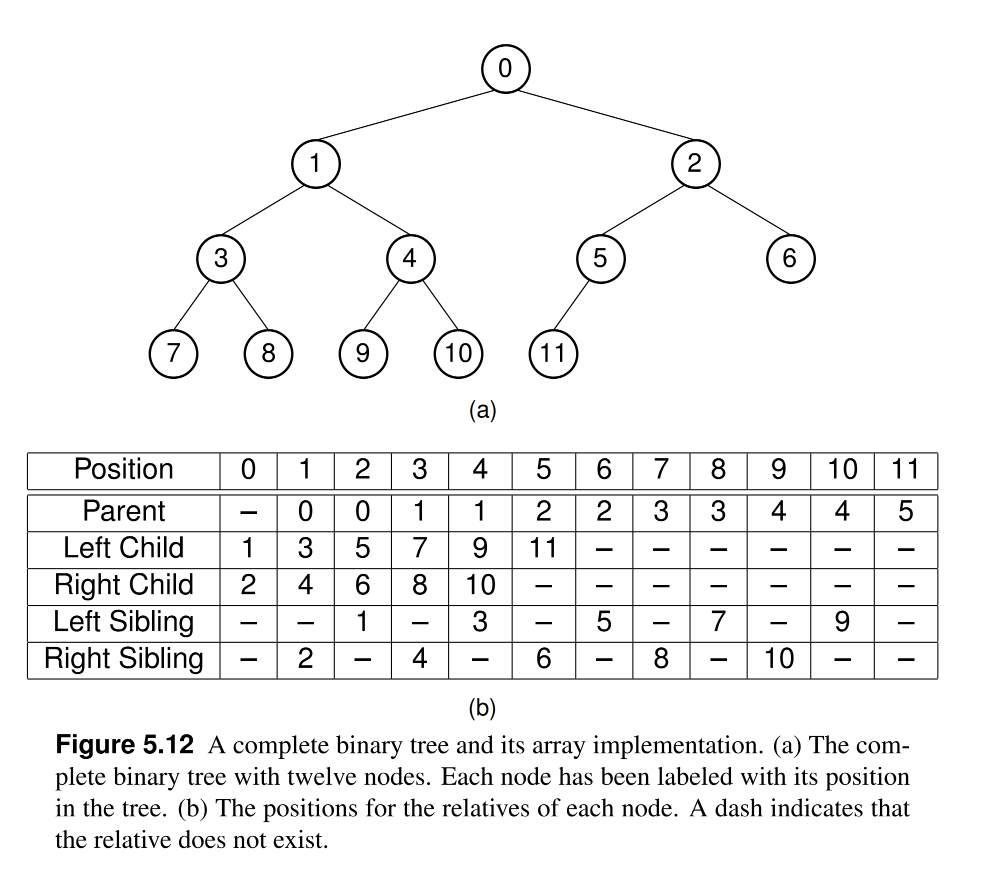
In a complete binary tree, the nodes are filled in array indices from left to right.
No need for pointers as we can calculate the index of the parent, left child, and right child of a node.
The only requirement is that the number of nodes (size) in known in advance, which is easy to achieve in a complete binary tree.
For any node at index:

   Parent(r) = floor((r - 1) / 2) // if r > 0
   LeftChild(r) = 2r + 1  // if 2r + 1 < n
   RightChild(r) = 2r + 2 // if 2r + 2 < n
   LeftSibling(r) = r - 1 // if r is even
   RightSibling(r) = r + 1 // if r is odd

5.4 Binary Search Trees¶

Dictionaries discussed in unit3 implemented based on sorted or unsorted arrays.
Dictionaries can be implemented using binary search trees (BSTs) to achieve O(log n) for all operations.

Operation	Sorted Array	Unsorted Array	BST	Comments for BST
insert	O(n)	O(1)	O(log n)	findPosition to insert, update parent
remove	O(n)	O(n)	O(log n)	findPosition to remove, update parent
find	O(log n)	O(n)	O(log n)	findPosition either in the left or right subtree

Binary Search Tree (BST):
- A tree that conforms to the Binary Search Tree property, listed below.
- All nodes stored in the right subtree of a node have keys greater than or equal to the key of that node.
- Traversing a BST in-order will result in a sorted list of keys.
Notes about BST:
- It is preferable to keep the BST as shallow as possible (lower height, balanced).
- The shape of tree depends in the insertion order.
- If elements are inserted in sorted order, the tree will be a linked list (one long branch with all nodes on the right, height is n).

/** Binary Search Tree implementation for Dictionary ADT */
class BST<Key extends Comparable<? super Key>, E> implements Dictionary<Key, E> {
    private BSTNode<Key, E> root; // Root of the BST
    private int nodeCount; // Number of nodes in the BST

    /** Constructor */
    BST() { root = null; nodeCount = 0; }

    /** Reinitialize tree */
    public void clear() { root = null; nodeCount = 0; }

    /**
     * Insert a record into the tree.
     *
     * @param k Key value of the record.
     * @param e The record to insert.
     */
    public void insert(Key k, E e) {
        root = insertHelp(root, k, e);
        nodeCount++;
    }

    /**
     * Remove a record from the tree.
     *
     * @param k Key value of record to remove.
     * @return The record removed, null if there is none.
     */
    public E remove(Key k) {
        E temp = findHelp(root, k); // First find it
        if (temp != null) {
            root = removeHelp(root, k); // Now remove it
            nodeCount--;
        }
        return temp;
    }

    /**
     * Remove and return the root node from the dictionary.
     *
     * @return The record removed, null if tree is empty.
     */
    public E removeAny() {
        if (root == null)
            return null;
        E temp = root.element();
        root = removeHelp(root, root.key());
        nodeCount--;
        return temp;
    }

    /**
     * @return Record with key value k, null if none exist.
     * @param k The key value to find.
     */
    public E find(Key k) { return findHelp(root, k); }

    /** @return The number of records in the dictionary. */
    public int size() { return nodeCount; }

    private E findHelp(BSTNode<Key, E> rt, Key k) {
        if (rt == null) return null;
        if (rt.key().compareTo(k) > 0)  return findHelp(rt.left(), k);
        else if (rt.key().compareTo(k) == 0) return rt.element();
        else return findHelp(rt.right(), k);
    }

    /**
     * @return The current subtree, modified to contain the new item
     */
    private BSTNode<Key, E> insertHelp(BSTNode<Key, E> rt, Key k, E e) {
        if (rt == null) return new BSTNode<Key, E>(k, e); // Empty tree: create node
        if (rt.key().compareTo(k) > 0) rt.setLeft(insertHelp(rt.left(), k, e));
        else rt.setRight(insertHelp(rt.right(), k, e));
        return rt; // Return tree with node inserted
    }

}

Removing a node from a BST or subtree¶

Removing a node from a BST is more complicated than inserting a node.
First, the node must be located (found), then removed. 3 cases to worry about:
1. if the node is a leaf, just remove it (this includes the root in a tree with only one node).
2. if the node has only one child, replace the node with its child.
3. if the node has two children, replace the node with the next largest node in the tree (the smallest node in its right subtree, or the largest value in the left subtree).

private BSTNode<Key,E> getMin(BSTNode<Key,E> rt) {
    if (rt.left() == null) return rt;
    return getMin(rt.left());
}

private BSTNode<Key,E> deleteMin(BSTNode<Key,E> rt) {
    if (rt.left() == null) return rt.right();
    rt.setLeft(deleteMin(rt.left()));
    return rt;
}

/** Remove a node with key value k @return The tree with the node removed */
private BSTNode<Key,E> removeHelp(BSTNode<Key,E> rt,Key k) {
    if (rt == null) return null;
    if (rt.key().compareTo(k) > 0) rt.setLeft(removeHelp(rt.left(), k));
    else if (rt.key().compareTo(k) < 0) rt.setRight(removeHelp(rt.right(), k));
    else { // Found it
        if (rt.left() == null) return rt.right();
        else if (rt.right() == null) return rt.left();
        else { // Two children
            BSTNode<Key,E> temp = getMin(rt.right());
            rt.setElement(temp.element());
            rt.setKey(temp.key());
            rt.setRight(deleteMin(rt.right()));
        }
    }
    return rt;
}

5.3 Heaps and Priority Queues¶

Priority Queues can be implemented based on a BST, sorted or unsorted array, or a heap.

Operation	Sorted Array	Unsorted Array	BST	Heap	Comments for Heap
insert	O(n)	O(1)	O(n log n)	O(log n)	insert at the end, then reHeapify
remove	O(n)	O(n)	O(n log n)	O(log n)	remove the root, place the last element at the root, then reHeapify
find	O(log n)	O(n)	O(log n)	O(n)	loop thorough elements one by one until a hit if found
dequeue	-	-	-	O(log n)	(removeMax or removeMin), call remove on the root, reHeapify

Heap:
- Heap is a complete binary tree (all levels are full except possibly the last level, and the last level is filled from left to right).
- It is always implemented as an array.
- Its values are partially ordered according to the heap property (in contrast to BST, where the values are totally ordered).
- There is no relationship between the values of nodes at the same level, the only relationship is between the parent and its children.
- Max-heap: the value of each node is greater than or equal to the value of its children (the largest value is at the root).
- Min-heap: the value of each node is less than or equal to the value of its children (the smallest value is at the root).
- HeapHeight = ceil(log(n+1))
- See MaxHeap Class Code
Insert:
1. Insert the new element at the end of the array.
2. Compare the new element with its parent according to the heap property, if the heap property is violated, swap the new element with its parent.
3. Repeat step 2 until the heap property is satisfied or the new element is the root.
Remove the root:
1. replace the root with the last element in the array.
2. Compare the new root with its children according to the heap property, if the heap property is violated, swap the new root with the larger child.
3. Repeat step 2 until the heap property is satisfied or the new root is a leaf.

5.6 Huffman Coding Trees¶

Huffman coding is a lossless data compression algorithm.
It assigns variable-length codes to input characters, based on the frequencies of their occurrence.
The most frequent character gets the smallest code and the least frequent character gets the largest code.
The variable-length codes assigned to input characters are Prefix Codes, means the codes (bit sequences) are assigned in such a way that the code assigned to one character is not the prefix of code assigned to any other character.

References¶

Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf. Chapter 5. ↩↩
Barnett, G. & Del Tongo, L. (2008). Data Structures and Algorithms: An Annotated Reference with Examples. Chapter 3: Binary Search Tree. ↩
UoPeople. (2023). CS 3303 Data Structures. Week 4: Binary Trees. Lecture Video. ↩
Barnett, G. & Del Tongo, L. (2008). Data Structures and Algorithms: An Annotated Reference with Examples. Chapter 4: Heap. ↩

4. Binary Trees¶

Introduction¶

Binary Search Tree (BST) 2¶

Tree Traversal¶

Heap 4¶

Heap Operations¶

5. Binary Trees 1¶

5.1.1 The Full Binary Tree Theorem¶

5.1.2 A Binary Tree Node ADT¶

5.2 Binary Tree Traversals¶

5.3 Binary Tree Node Implementations¶

Mathematical Expressions as Binary Trees¶

Space Requirements for Binary Trees¶

5.3.3 Array Implementation for Complete Binary Trees¶

5.4 Binary Search Trees¶

Removing a node from a BST or subtree¶

5.3 Heaps and Priority Queues¶

5.6 Huffman Coding Trees¶

References¶

Binary Search Tree (BST) ²¶

Heap ⁴¶

5. Binary Trees ¹¶