Skip to content

WA1. Set Exercises

1. Explain the following basic concepts in sets with an example for each

  1. Finite set: Is a set with a finite number of elements, and its cardinality is exactly defined. Example: The set of all file names in a directory.
  2. Infinite set: It is a set with an infinite number of elements, and its cardinality is not defined. Example: The set of all positive integers as it has \(\infty\) elements.
  3. Null set: It is a set with no elements, and its cardinality is 0. Example: The empty set \(\emptyset\).
  4. Singleton set: It is a set with only one element, and its cardinality is 1. Example: \(A = \{1\}\).
  5. Subset: It is a part of a set, all its members are also of the original set, and the subset may hold all items from the original set, that is every set is subset of itself. Example: The set \(A = \{1, 2\}\) is a subset of the set \(B = \{1, 2, 3\}\).
  6. Superset: It is the counter part to the subset, if \(A\) is a subset of \(B\), then \(B\) is a superset of \(A\). Example: The set \(B = \{1, 2, 3\}\) is a superset of the set \(A = \{1, 2\}\).
  7. Proper set: It is a similar to the subset, however, the subset must have smaller cardinality than the original one, and it can not be equal to the original set. Example: The set \(A = \{1, 2\}\) is a proper subset of the set \(B = \{1, 2, 3\}\), but not a proper subset of itself.
  8. Universal set: It is a set that holds all possible elements from all sets within the context. Example: The set of all items in a store.
  9. Power set: It is a set that holds all the possible subsets of a set, the empty set is always a part of the power set. Example: The power set of the set \(A = \{1, 2\}\) is \(P(A) = \{\emptyset, \{1\}, \{2\}, \{1, 2\} \}\).
  10. The Cardinality of a set: The number of elements within the set. Example: The cardinality of the set \(A = \{1, 2, 3\}\) is 3.

2. Create a Venn Diagram to show A- (B ∪ C) = (A-B) ∩(A-C), for any non-empty sets A, B, and C and one of De Morgan’s identities

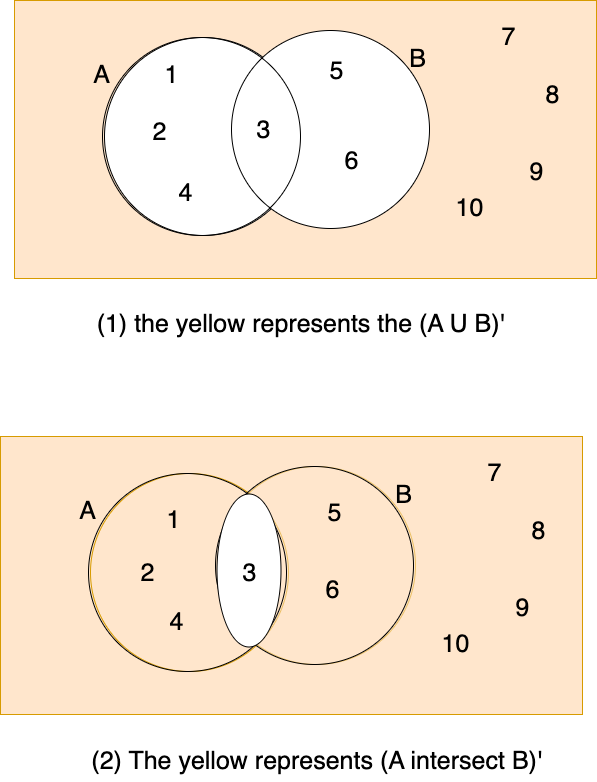
3. Create two different sets A and B of your choice, say the cardinality of A and B respectively are |A|, |B|. What are the smallest and largest possible values of the following sets?

  1. (a) |A ∪B|
  2. (b) |A ∩B|
  3. © |A × B|

Let’s assume that \(|A| = 3\) and \(|B| = 4\) and \(A = \{1, 2, 3\}\) and \(B = \{1, 2, 3, 4\}\)

|A ∪ B|

  • As union is the combination of both sets, the result set must be at least the size of the largest set, which is \(|B| = 4\) and at most the sum of both sets, which is \(|A| + |B| = 3 + 4 = 7\)
  • \[|A ∪ B| = |A| + |B| - |A ∩ B| = 3 + 4 - 3 = 4\]
  • \[|A ∪ B| = \{1, 2, 3, 4\} \]

|A ∩ B|

  • As intersection is the common elements between both sets, the result set must be at most the size of the smallest set, which is \(|A| = 3\) and at least 0, as the sets may not have any common elements.
  • \[|A ∩ B| = |A| + |B| - |A ∪ B| = 3 + 4 - 4 = 3\]
  • \[|A ∩ B| = \{1, 2, 3\} \]

|A × B|

  • As the Cartesian product is the combination of all elements in both sets, the result set must be at exactly the product of both sets cardinalities, which is \(|A| \times |B| = 3 \times 4 = 12\).
  • Thus, the most possible cardinality results from the Cartesian product.

4. Society of 160 families

In a society of 160 families, it was found that 123 families watch Netflix; 124 families watch Hulu; 110 families watch Amazon Prime video; 119 families watch both Amazon Prime video and Netflix; 111 families watch Netflix and Hulu; 81 families watch Hulu and Amazon Prime video; and 143 families watch all the 3 platforms. Find:

Platform Families
N 123
H 124
A 110
N ∩ A 119
N ∩ H 111
H ∩ A 81
N ∩ H ∩ A 143

1. The number of families who watch at least one platform

The number of families who watch at least one platform is the number of families who watch Netflix, Hulu, or Amazon Prime video, which is the union of all three sets.

\[ \begin{align} |N ∪ H ∪ A| & = \\ & = |N| + |H| + |A| - |N ∩ H| - |N ∩ A| - |H ∩ A| + |N ∩ H ∩ A| \\ & = 123 + 124 + 110 - 111 - 119 - 81 + 143 \\ & = 489 - 311 \\ & = 178 \end{align} \]

2. The number of families who watch exactly one platform

The number of families who watch exactly one platform is the number of families who watch Netflix, Hulu, or Amazon Prime video, but not both, which is the union of all three sets, minus the intersection of all three sets.

\[ \begin{align} |N ∪ H ∪ A| - |N ∩ H ∩ A| &= 178 - 143 = 35 \\ & = 35 \end{align} \]

References

  • Doerr, A., & Levasseur, K. (2022). Applied discrete structures (3rd ed.). licensed under CC BY-NC-SA. Chapter 4: More on Sets.
  • Levin, O. (2021). Discrete mathematics: An open introduction (3rd ed.). licensed under CC 4.0. Chapter 0: Introduction.