JA3. Derivation

Question 1

1. Using the limit definition of derivative, find \(f'(3)\) for the function \(f(x) = x^3+17x^2-12x+2\).

\[ \begin{aligned} f'(x) &= 3x^2+34x-12 \\ f'(3) &= 3(3)^2+34(3)-12 \\ &= 27+102-12 \\ &= 117 \end{aligned} \]

Question 2

2. Find the slope of the secant line between the values 3 and 4 for the function \(f(x) = x^4\).

\[ \begin{aligned} m &= \frac{f(4)-f(3)}{4-3} \\ &= \frac{4^4-3^4}{4-3} \\ &= \frac{256-81}{1} \\ &= 175 \end{aligned} \]

Question 3

3. Applying limit definition of derivative, find the slope of the tangent line \(f(x) = x^4\) at \(x=3\).

\[ \begin{aligned} m &= \lim_{h \to 0} \frac{f(3+h)-f(3)}{h} \\ &= \lim_{h \to 0} \frac{(3+h)^4-3^4}{h} \\ &= \lim_{h \to 0} \frac{81+108h+54h^2+12h^3+h^4-81}{h} \\ &= \lim_{h \to 0} \frac{108h+54h^2+12h^3+h^4}{h} \\ &= \lim_{h \to 0} 108+54h+12h^2+h^3 \\ &= 108 \end{aligned} \]

Question 4

4. What do you understand from question numbers 2 and 3 about secant lines and tangent lines? Explain any difference or any similarity.

The slope of the secant line is the average rate of change of the function between the two points. The slope of the tangent line is the instantaneous rate of change of the function at a point.

Question 5

5. The total cost of producing x winter jackets in dollars is given by \(C(x) = 100 + 10x + 0.2x^2\) using the limit definition of the derivative, find average cost per jacket in \([10,12]\). Then find the average cost of making 1500 jackets.

\[ \begin{aligned} \text{Average cost per jacket} &= \frac{C(12)-C(10)}{12-10} \\ &= \frac{100+10(12)+0.2(12)^2-100-10(10)-0.2(10)^2}{2} \\ &= \frac{100+120+28.8-100-100-20}{2} \\ &= \frac{28.8}{2} \\ &= 14.4 \end{aligned} \]

\[ \begin{aligned} \text{Average cost of making 1500 jackets} &= \frac{C(1500)-C(0)}{1500-0} \\ &= \frac{100+10(1500)+0.2(1500)^2-100-10(0)-0.2(0)^2}{1500} \\ &= \frac{100+15000+4500000-100}{1500} \\ &= \frac{4510000}{1500} \\ &= 3006.67 \end{aligned} \]

Question 6

6. Apply the derivative rules, find \(f'(x)\) for \(f(x) = (x + 2) ( x^2 + 16x + 4)\).

\[ \begin{aligned} f'(x) &= (x^2+16x+4) + (x+2)(2x+16) \\ &= x^2+16x+4+2x^2+32x+4x+32 \\ &= 3x^2+52x+36 \end{aligned} \]

Question 7

7. Apply the derivatives rules, find \(f'(x)\) for \(f(x) = \frac{x^4-5x^3+2x^2-5}{3x^2}\).

\[ \begin{aligned} f'(x) &= \frac{(x^4-5x^3+2x^2-5)'(3x^2)-(x^4-5x^3+2x^2-5)(3x^2)'}{(3x^2)^2} \\ &= \frac{(4x^3-15x^2+4x)(3x^2)-(x^4-5x^3+2x^2-5)(6x)}{(3x^2)^2} \\ &= \frac{12x^5-45x^4+12x^3-18x^5+90x^4-36x^3+24x^3-120x^2+48x}{9x^4} \\ &= \frac{-6x^5+135x^4-12x^3-120x^2+48x}{9x^4} \\ &= \frac{-2x^5+45x^4-4x^3-40x^2+16x}{3x^4} \end{aligned} \]

Question 8

8. Find the equation of the tangent line to the graph of \(f(x) = (x + 2) ( x^3 - 5x - 1)\) at \(x=1\).

\[ \begin{aligned} f'(x) &= (x^3-5x-1)+(x+2)(3x^2-5) \\ &= x^3-5x-1+3x^3-5x+6x^2-10 \\ &= 4x^3+6x^2-10x-11 \\ f'(1) &= 4(1)^3+6(1)^2-10(1)-11 \\ &= 4+6-10-11 \\ &= -11 \end{aligned} \]

Question 9

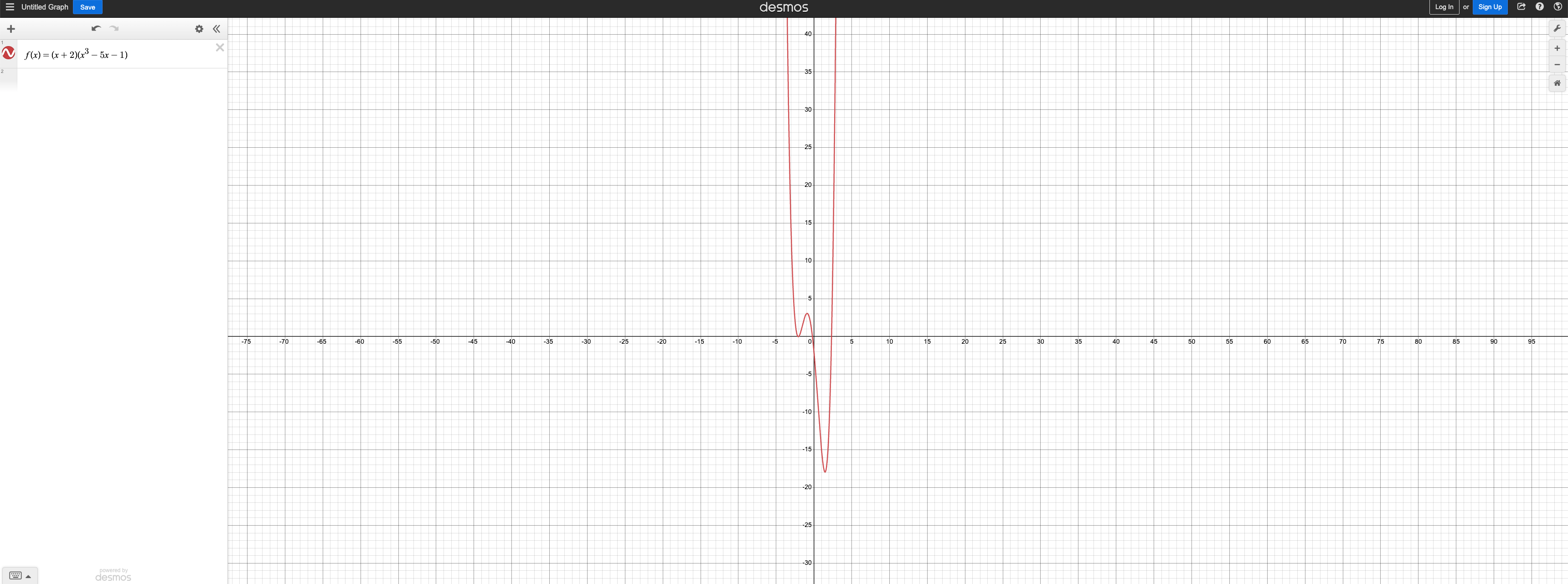
9. Use Desmos graphing calculator to graph the function \(f(x) = (x + 2) ( x^3 - 5x - 1)\).

Question 10

10. The concentration of antibiotic in the bloodstream t hours after being injected is given by the function \(C(t)\) is measured in milligrams per litre of blood. Find the rate of change of \(C(t) = \frac{ t^2 + 4}{2t}\). Determine the rate of change for \(t=2\) hours.

\[ \begin{aligned} C'(t) &= \frac{(t^2+4)'(2t)-(t^2+4)(2t)'}{(2t)^2} \\ &= \frac{(2t)(2t)-(t^2+4)(2)}{(2t)^2} \\ &= \frac{4t^2-2t^2-8}{4t^2} \\ &= \frac{2t^2-8}{4t^2} \\ &= \frac{t^2-4}{2t^2} \\ C'(2) &= \frac{(2)^2-4}{2(2)^2} \\ &= \frac{4-4}{8} \\ &= 0 \end{aligned} \]