Skip to content

DA4. Discussion Assignment 4

Statement

For your discussion post, explain your process for each of the following steps:

  1. Define constraint satisfaction problem (CSP) in terms of variables, domains, and constraints.
  2. Then consider the N-Queen Problem (N number of queens should be placed in an N X N matrix such that no queen shares the same row, column, or diagonal). Convert this problem to CSP by creating a variable set, domain set, and constraint set.
  3. Construct a search space in the form of a graph from which the search strategy can be used from the above information. Feel free to upload any hand diagram or graph.
  4. Finally identify the search strategy/algorithm that you would recommend to solve this problem and explain why you selected the strategy?

Answer

1. Define constraint satisfaction problem (CSP) in terms of variables, domains, and constraints

A variable is a name to a feature, and accepts values to be assigned to the name; where the set of all possible values are called the domain of a variable. For example, let x: int = 1; here x is a variable and 1 is the value assigned to x from its domain of integers.

A constraint specifies legal combinations of assignments of values to some of the variables; that is, a condition that defines which values of the domain can be assigned to the variables. The set of variables involved in the constraint is the scope of the constraint. When the condition of the constraint evaluates to true then the constraint is satisfied, otherwise it is violated (Poole & Mackworth, 2017).

A constraint satisfaction problem (CSP) consists of a set of variables, a domain for each variable, and a set of constraints. A solution is a total assignment that satisfies all of the constraints. There are multiple methods to solve a CSP, such as generate-and-test algorithms, local search, hill climbing, stochastic local search, simulated annealing, and minimax algorithm (Taipala, 2014).

2. N-Queen Problem to CSP

The N-Queen problem defines a matrix of size N X N, where N queens should be placed such that no queen shares the same row, column, or diagonal. The problem can be converted to a CSP by defining the following:

  • Variable set: Q1, Q2, Q3, ..., QN where Qi represents the queen in the i-th row.
  • Domain set: d⁢o⁢m⁢(Qi) = {1, 2, 3, ..., N} where Qi can take values from 1 to N.
  • Constraint set: C = {C1, C2, C3, ..., CN} where Ci represents the constraint that no two queens share the same row, column, or diagonal; where each Ci = {Qi ≠ Ip, Qj ≠ Jp, |Qi - Qj| ≠ |Ip - Jp|} as:
    • Qi and Qj are the queens in the i-th row and j-th column.
    • Ip and Jp are all the i-th and j-th rows and columns occupied by previous queens.
    • |Qi - Qj| ≠ |Ip - Jp| ensures that no two queens share the same diagonal.

We can type the constraints in a more formal way as follows:

X = {Q1, Q2, Q3, ..., QN}
D = {1, 2, 3, ..., N} for each Qi in X
C = {
    <Qi, (Qi ≠ Ip for each i, p in 1 to i-1)>,
    <Qj, (Qj ≠ Jp for each j, p in 1 to i-1)>,
    <Qi, Qj, |Qi - Qj| ≠ |Ip - Jp| for each i, j, p in 1 to i-1>
}

3. Construct a search space in the form of a graph

The images below represent the search space of the problem with a chosen example of N=4. It starts with an empty board of 4 X 4, and all places are empty. We start by placing the first queen at (1, 1) and the squares that are no longer allowed are marked with an ❌, we do the same for every queen until we reach the 4th queen.

Image 1: Empty board + Q1
Q1
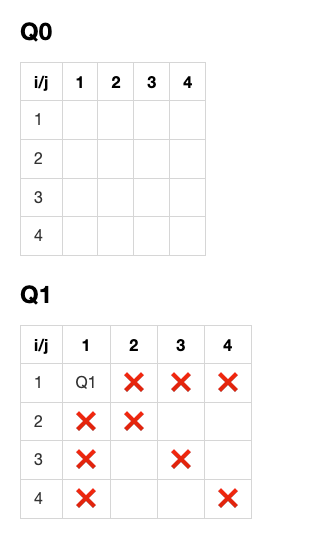Image 2: Q2 + Q3
Q2
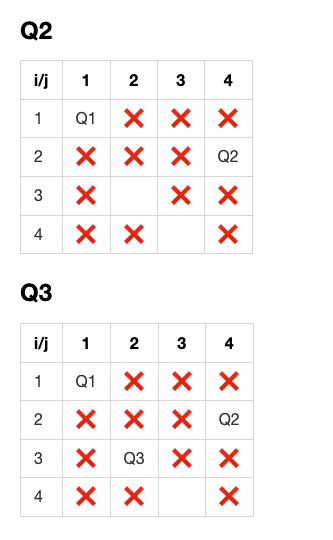Image 3: Q4
Q3

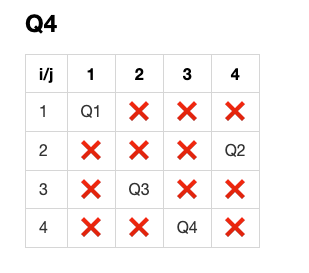The tables above represent 5 different states of the board, each of them relies on the state of the previous board; and we notice that the search space is getting smaller after every placement of a queen (if we successfully exclude the invalid squares from the search algorithm).

4. Search strategy/algorithm recommendation

A suitable search strategy to solve the problem avoiding the brute force approach is to use a local search algorithm, such as hill climbing or other backtracking techniques. The idea is simple, and that is to exclude the invalid squares after each placement; for example, in the image above, after placing Q1 at (1, 1), we should exclude all the squares with i = 1, j = 1, |i - j| = 0, and |i + j| = 2 (row, column, and diagonal). This way, we can reduce the search space and find a solution faster.

An effective algorithm would be to place the first queen at (1,1), and then increase i by 1; and turn the problem into a local search problem within all the squares of that row; we place the next queen at the first allowed square. Then, we go down one row, and look within the columns of that row for the next queen, and so on.

References