Skip to content

DA2. Algorithm Analysis

Statement

  • For the following problems, develop your answers and post your answers to the discussion forum.
  • Asymptotic analysis is a difficult concept to master as such we will all benefit by understanding each other’s perspectives.

Problem 1

  • Suppose that algorithm A takes 1000n3 steps and algorithm B takes 2n steps for a problem of size n. For what size of the problem is algorithm A faster than B (meaning algorithm A has fewer steps than B)?
  • In your answer describe not only what the answer is but how you arrived at the answer.

Answer 1

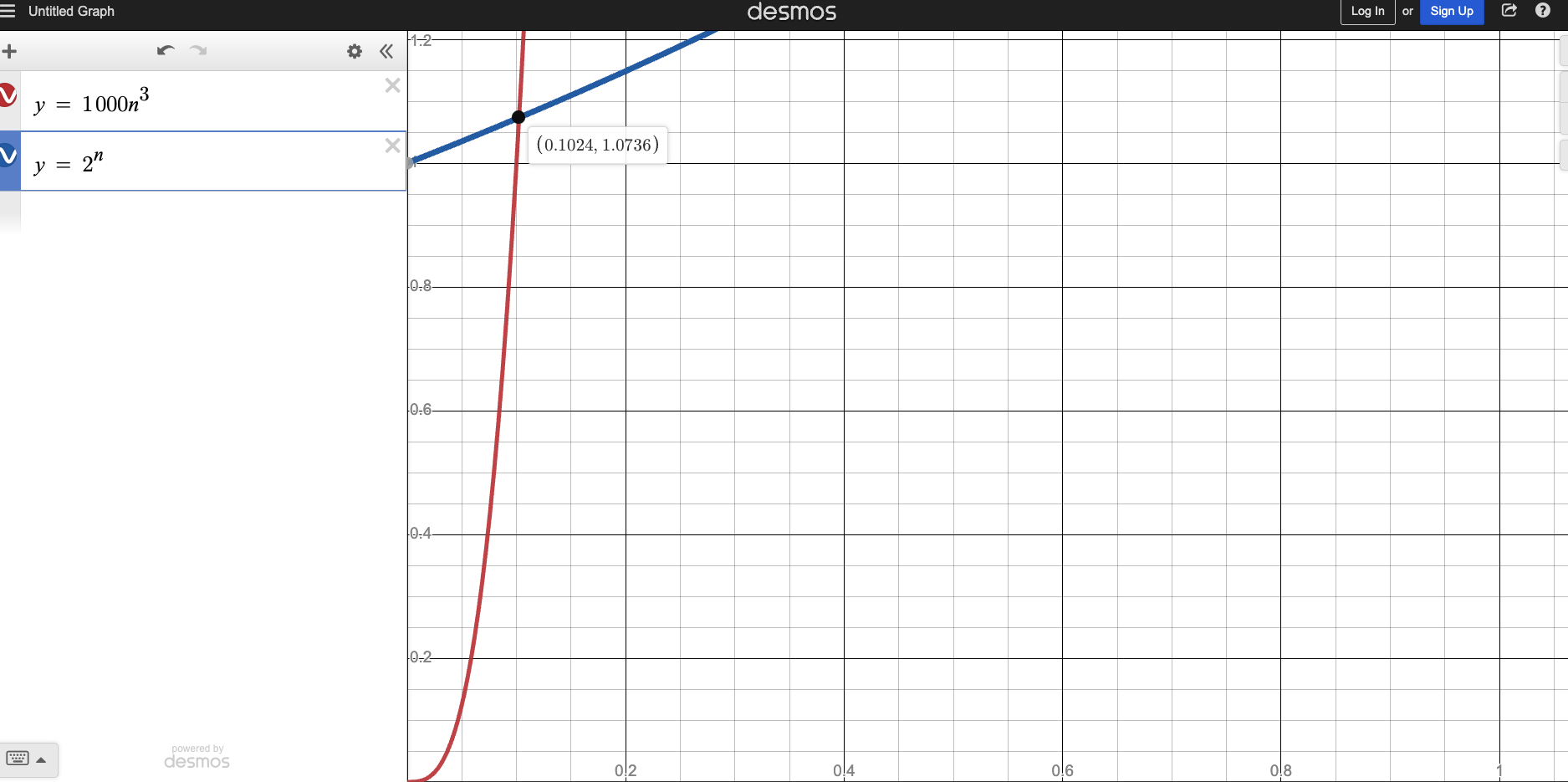
  • The plan is to sketch the two functions and find the point where A is faster than B (A graph is below B graph).
  • In the sketch below, the X axis is the input size and the Y axis is the number of steps.
  • The red line is the A = 1000n^3 function and the blue line is the B = 2^n function.
  • The two graphs intersect at two points: (0.1, 1.07) and (24.6, 1.0324 * 10^7)
  • We will study the graph in 3 different parts:
    • Part 1: n between 0 and 1
    • Part 2: n between 1 and 24
    • Part 3: n > 24
Part 1 - n between 0 and 1

sketching

  • B = 2^n (blue line) is above A = 1000n^3 (red line) for all values of n between 0 and 1.
  • No input size of n is between 0 and 1, so we ignore this part.
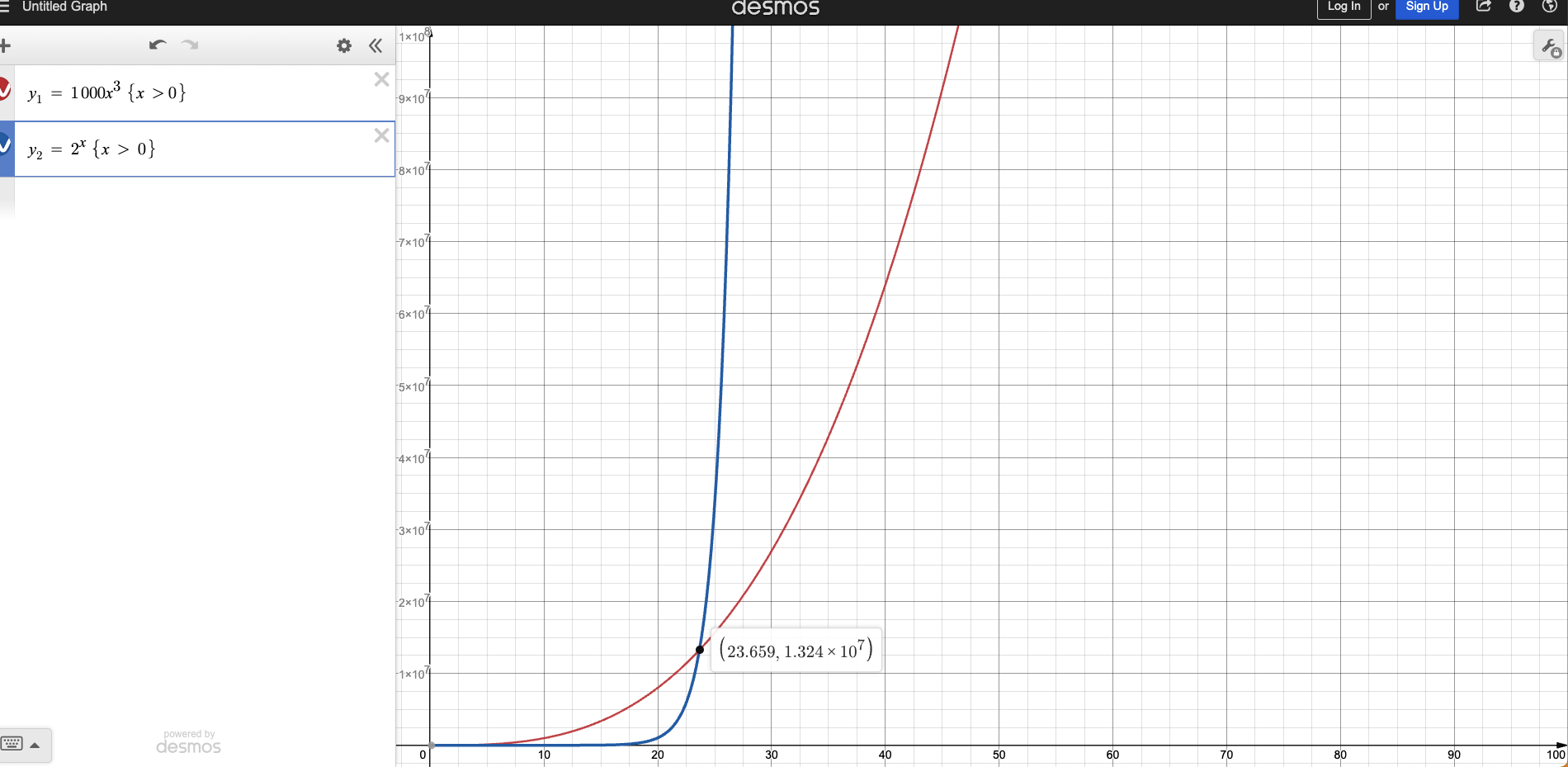
Part 2 - n between 1 and 24

sketching

  • B = 2^n (blue line) is above A = 1000n^3 (red line) for all values of n between 1 and 24.
  • We conclude that B = 2^n is always faster than A = 1000n^3 for all values of n between 1 and 24.
Part 3 - n > 24

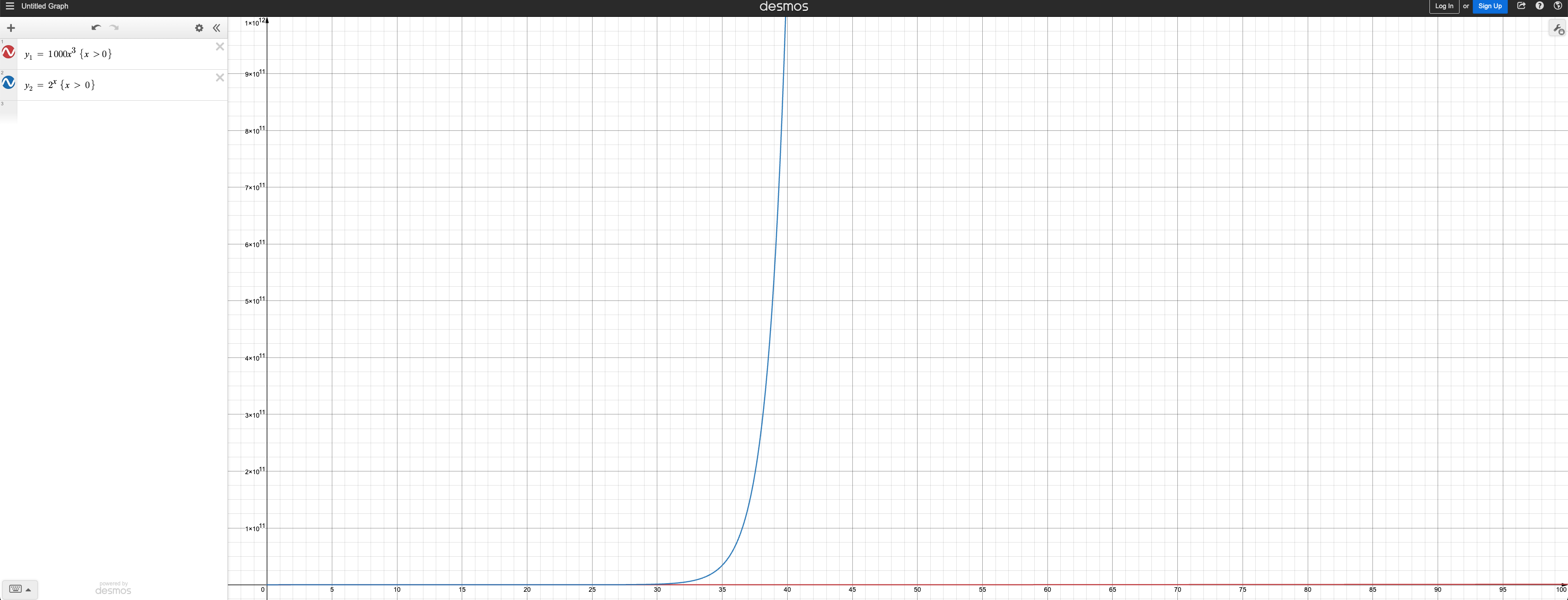
sketching

  • B = 2^n (blue line) is above A = 1000n^3 (red line) for all values of n greater than 24.
  • The difference between the two graphs is super huge once n exceeds 30.
Conclusion
  • We saw that B = 2^n is faster than A = 1000n^3 for all values of n between 1 and 24.
  • But we also saw that B = 2^n is faster than A = 1000n^3 for all values of n greater than 24.
  • Because the domain n > 24 is much more significant than the domain n between 1 and 24, we can conclude that A = 1000n^3 is faster (in genral) than B = 2^n.
  • Also, we can safely say that factorial growth is always slower than exponential growth.

Problem 2

  • Give the upper bound (big O notation) that you can for the following code fragment, as a function of the initial value of n.
for(int i = 0; i < n; i++) {
    for(int j = 0; j < i; j++){
        //do swap stuff, constant time
    }
}
  • Do you think that the lower bound is likely to be the same as the answer you gave for the upper bound?
  • In your response state why or why not.

Answer 2

  • Looking at the nested for loops, we can see:
    • The outer loop runs n times
    • The inner loop runs i times that is i = 0, 1, 2, …, n-1 which is almost n/2 times (Shaffer, 2011, Example 3.12)
    • The total cost for this code fragment is n×12n=12n2.
  • The Upper bound is O(n2) where the constant 1/2 is ignored.
  • The lower bound is also O(n2)
  • Since both the upper and lower bounds are the same, we can represent the time complexity of this code fragment as θ(n2).

References