Skip to content

DA8. Definite Integrals

Statement

For the discussion item this week, explain in your own words how the definite integral can be used to determine at least 2 different things? For example, it could be used to determine profit over a given period or to calculate total distance traveled over a certain time, or it could be any other topic of your choice. Take a moment and review problems 214-253 in section 5.4 if you need ideas.

Solution

A definite integral is either a number (when the limits of integration are constants) or a single function (when one or both of the limits of integration are variables) (Herman & Strang, 2020, p. 566).

The net change theorem considers the integral of a rate of change. It says that when a quantity changes, the new value equals the initial value plus the integral of the rate of change of that quantity (Herman & Strang, 2020, p. 567).

\[ \int_{a}^{b} F'(x) \, dx = F(b) - F(a) \]

Where \(F(x)\) is the antiderivative of \(f(x)\).

The main use of the definite integral is to calculate the area under a curve, which may mean different things according to the domain of the problem; for example, the area under a curve may represent the displacement of an object, the profit of a company, or the amount of water in a tank (Herman & Strang, 2020).

The first example this text will discuss is the problem 238. Newton’s law of gravity states that the gravitational force exerted by an object of mass M and one of mass m with centers that are separated by a distance r is F = G(mM/r^2).

Considering the masses of the two objects and G are constants, we can assume c = GmM and rewrite the function to F = c/r^2, and we will assume c =1, now we can use the function f(r) = 1/r^2 that represents the distance on the x-axis and work (or the force) that is required to move the object from the origin to the distance r.

For example, the total force required to move the objects from distance 1 to distance 2 from each other is shown below in the green highlighted area.

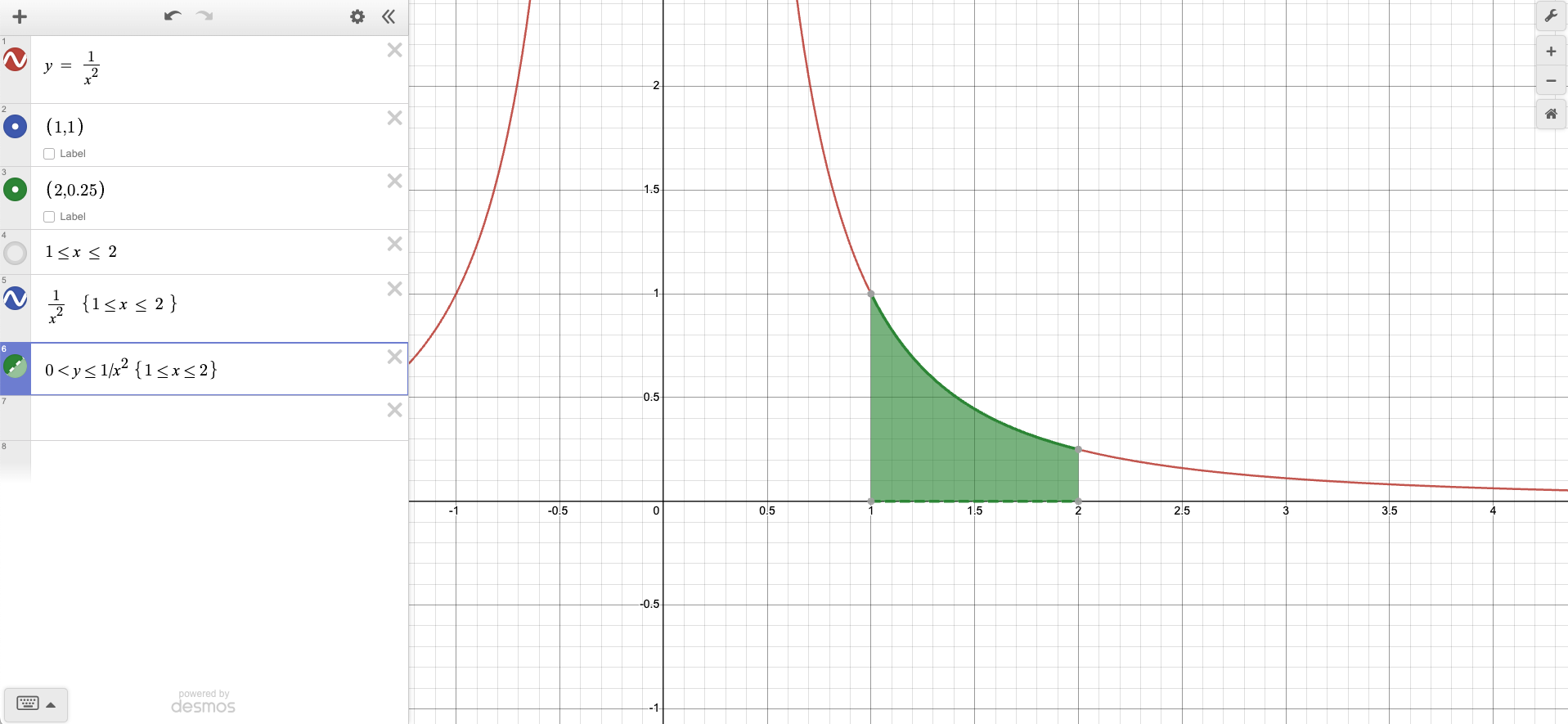
And can be calculated by the definite integral:

\[ \int_{1}^{2} \frac{1}{r^2} \, dr = \left[ -\frac{1}{r} \right]_{1}^{2} = -\frac{1}{2} + \frac{1}{1} = \frac{1}{2} \]

Putting back the constant c, we have:

\[ \int_{1}^{2} \frac{c}{r^2} \, dr = \left[ -\frac{c}{r} \right]_{1}^{2} = -\frac{c}{2} + \frac{c}{1} = \frac{c}{2} = \frac{GmM}{2} \]

The curve above aligns with our intuition, as the force becomes smaller and smaller as the distance increases when the gravity of the objects no longer affects each other.

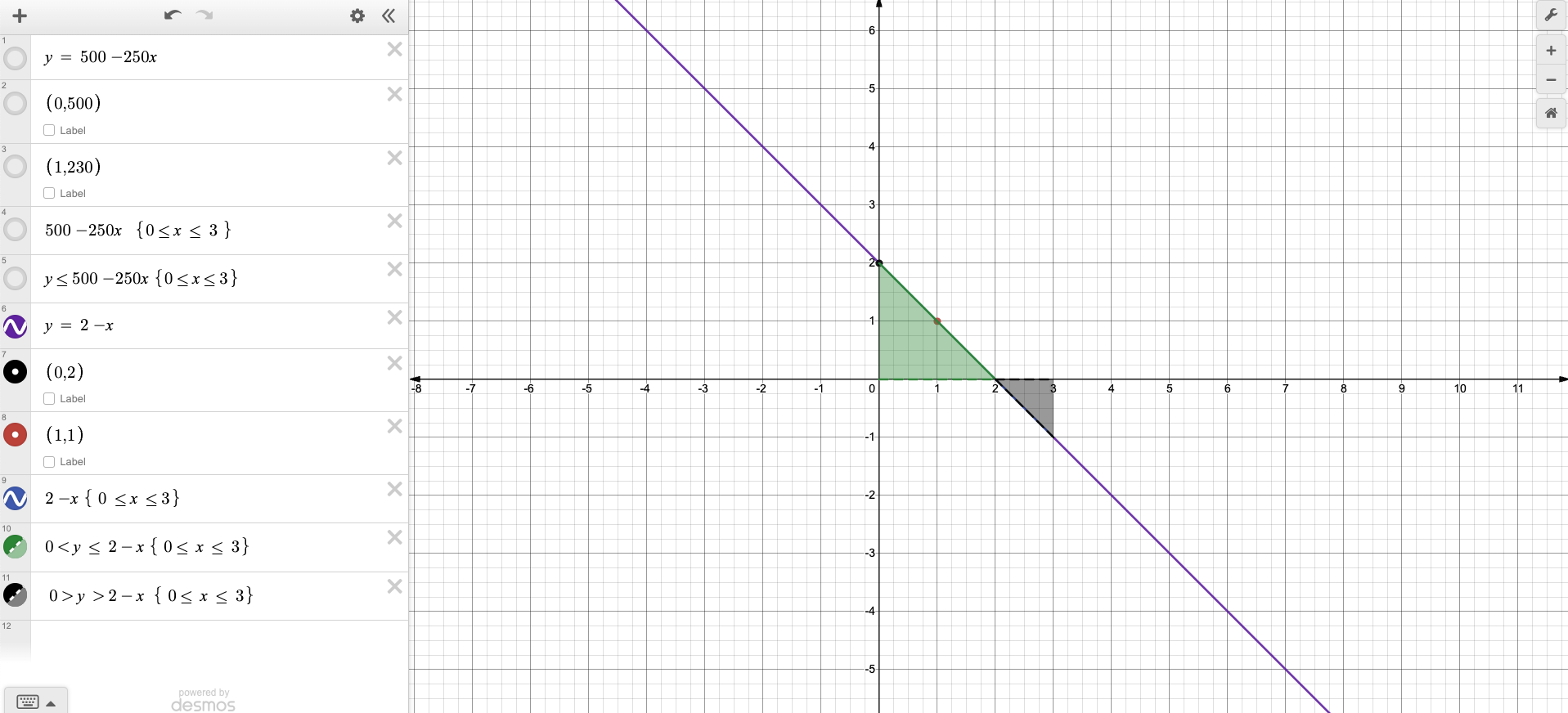
The second example is the problem 240. John burns 500 - 50t calories when he is riding his bike while eating 4t cookies with 50 calories each.

The formula to calculate the total calories burned is:

\[ \begin{aligned} \text{total calories} &= (500 - 50t) - 4(50)t \\ &= 500 - 250t \end{aligned} \]

The graph was not clear enough to show the area under the curve, so I will use a simplified version of the function as:

\[ \text{total calories} = 2 - t \]

The total calories burned during the first 3 hours can be calculated by the definite integral:

\[ \begin{aligned} \text{total calories} &= \int_{0}^{3} (2-t) \, dt \\ &= \left[ 2t - \frac{t^2}{2} \right]_{0}^{3} \\ &= 6 - \frac{9}{2} = \frac{3}{2} \end{aligned} \]

The graph below shows the area under the curve in the green highlighted area minus the area highlighted in black, which represents a time where calories consumed is greater than calories burned.

References