6. Internal Sorting Techniques and Algorithms¶

Introduction ¹ ²¶

Sorting is the process of arranging a collection of elements in a particular order.
Algorithms that uses Divide and Conquer:
- Merge Sort: divides a list in halves.
- Quick Sort: divides a list into big and small elements.
- Radix Sort: divides a list into digits, by working on digit of the key at a time.
Sorting in general is an O(n log n) problem in the worst case.
Assumptions in this unit:
- All inputs to the sorting algorithms discussed in this unit must extend the Comparable class by implementing the compareTo method.
- For every record type, a swap functions must be defined to swap two records in the array.
Sorting Problem:
- Given a list of records that have keys, and values, sort the records by their keys in ascending order.
- Duplicate input keys are allowed.
- Duplicated keys are sorted by their occurrence in the original list, the original order of duplicated keys is preserved.
- All keys in the keys are of fixed length and of the same type.
Stable Sorting algorithm: preserves the original order of duplicated keys.
The runtime of a sorting algorithm depends on:
- The number of records to be sorted.
- The initial order of the records.
- The size of keys and records.
- The allowable range of keys.
Sorting algorithm analysis measures:
- Comparisons count.
- Swaps count.
The CompareTo method gets called as caller.compareTo(parameter), where caller and parameter must be of the same type, and returns:
- Negative if the caller is less than the parameter.
- Zero if the caller is equal to the parameter.
- Positive if the caller is greater than the parameter.

7.2 Three Θ(n2) Sorting Algorithms¶

7.2.1 Insertion Sort¶

static <E extends Comparable<? super E>> void inssort(E[] A) {
    for (int i=1; i<A.length; i++) // Insert i’th record
        for (int j=i; (j>0) && (A[j].compareTo(A[j-1])<0); j--)
            DSutil.swap(A, j, j-1);
}

Worst case: all keys are in reverse order (descending) which has a time complexity of Θ(n2) as the inner loop will always execute i times.
Best Case: all keys are in ascending order which has a time complexity of Θ(n) as the inner loop will never execute
The worst case is more common than the best case, but the best case can be encountered for slightly disordered lists.
Slightly disordered lists are lists that are almost sorted, but have a few elements out of order, e.g. after a few insertions into a sorted list.
Algorithms that take advantages of Insertion Sort near-best-case running time: Shell Sort and Quick Sort.

case	time complexity	comparisons	swaps
worst	Θ(n2)	n^2	n^2 - n
best	Θ(n)	n	0
avg	Θ(n2)	Θ(n2)	Θ(n2)

7.2.2 Bubble Sort¶

It is a very slow sorting algorithm, that has no practical use.

static <E extends Comparable<? super E>> void bubblesort(E[] A) {
    for (int i=0; i<A.length-1; i++) // Bubble up i’th record
        for (int j=A.length-1; j>i; j--)
            if ((A[j].compareTo(A[j-1]) < 0))
                DSutil.swap(A, j, j-1);
}

Average, worst, and best case are almost the same regardless of the initial order of the records.
Number of swaps is identical to the swaps count in Insertion Sort.

7.2.3 Selection Sort¶

Sorts the list by repeatedly finding the smallest element in the unsorted part of the list and moving it to the end of the sorted part of the list.
It does a relatively smaller number of swaps than previous two that equals to n-1.

static <E extends Comparable<? super E>> void selectsort(E[] A) {
    for (int i=0; i<A.length-1; i++) { // Select i’th record
        int lowindex = i; // Remember its index
        for (int j=A.length-1; j>i; j--) // Find the least value
            if (A[j].compareTo(A[lowindex]) < 0)
                lowindex = j; // Put it in place
                DSutil.swap(A, i, lowindex);
    }
}

Most useful when the cost of a swap is high, e.g. when the records are large strings or objects.

7.2.4 The Cost of Exchange Sorting¶

Exchange is the process of swapping two adjacent records.
Inversion:
- is a pair of records that are out of order.
- The number of inversions for an element, is the number of elements that are greater than it and appear before it in the list.
- All inversions must be moved to the right of the element to consider it in the correct position in the sorted list.
- The average number of inversions for a list is n(n-1)/4 = Omega(n2) in the average case.
The Insertion, Bubble, and Selection sorts are exchange sorts.
The number of comparisons

- Insertion Bubble Selection

best case Θ(n) Θ(n2) Θ(n2)

avg case Θ(n2) Θ(n2) Θ(n2)

worst case Θ(n2) Θ(n2) Θ(n2)
The number of swaps

- Insertion Bubble Selection

best case 0 0 Θ(n)

avg case Θ(n2) Θ(n2) Θ(n)

worst case Θ(n2) Θ(n2) Θ(n)

7.3 Shell Sort¶

static <E extends Comparable<? super E>> void shellsort(E[] A) {
    for (int i=A.length/2; i>2; i/=2) // For each increment
        for (int j=0; j<i; j++) // Sort each sublist
            inssort2(A, j, i);
    inssort2(A, 0, 1); // Could call regular inssort here, final pass
}

/** Modified Insertion Sort for varying increments */
static <E extends Comparable<? super E>> void inssort2(E[] A, int start, int incr) {
    for (int i=start+incr; i<A.length; i+=incr)
        for (int j=i; (j>=incr)&& (A[j].compareTo(A[j-incr])<0); j-=incr)
            DSutil.swap(A, j, j-incr);
}

Shell Sort is called diminishing increment sort, because it uses a sequence of increments that diminish to 1, at which point the list is sorted.
Inventor: Donald Shell (1959).
It is a non-exchange sort, because it does swap non-adjacent elements.
Shell Sort is an incremental version of Insertion Sort.
It divides the list into sublists and sorts each sublist using Insertion Sort, resulting in a near-sorted list that can be quickly sorted using Insertion Sort on the entire list.
The efficiency of the algorithm depends on the increment sequence, with 2 or 3 being the most common.
It is proven that the most effective sequence is 3 resulting in O(n3/2) or O(n^1.5) time complexity.

7.4 Merge Sort¶

static <E extends Comparable<? super E>> void mergesort(E[] A, E[] temp, int l, int r) {
    int mid = (l+r)/2; // Select midpoint
    if (l == r) return; // List has one element

    mergesort(A, temp, l, mid); // Mergesort first half
    mergesort(A, temp, mid+1, r); // Mergesort second half

    for (int i=l; i<=r; i++) // Copy subarray to temp
        temp[i] = A[i];

    // Do the merge operation back to A
    int i1 = l; int i2 = mid + 1;
    for (int curr=l; curr<=r; curr++) {
        if (i1 == mid+1) // Left sublist exhausted
            A[curr] = temp[i2++];
        else if (i2 > r) // Right sublist exhausted
            A[curr] = temp[i1++];
        else if (temp[i1].compareTo(temp[i2])<0) // Get smaller
            A[curr] = temp[i1++];
        else A[curr] = temp[i2++];
    }
}

Best for sorting linked lists since it does not require random access to the elements.
It requires twice the space of the original list.
Time complexity is O(n log n).
If the input is a linked list:
- Merging two sorted lists is easy, remove the node from the front of the list with the smaller key and add it to the end of the new list.
- Dividing the linked list into two halves is challenging, as it requires a traversal of the list to find the middle.
- The division can work by traversing the list, adding every odd node to the first list and every even node to the second list (or vice versa).
If the input is an array:
- Splitting it into two halves is easy and fast, using the index of the middle element.
- Merging the two sorted elements is also easy.

static <E extends Comparable<? super E>> void mergesort(E[] A, E[] temp, int l, int r) {
    int i, j, k, mid = (l+r)/2; // Select the midpoint
    if (l == r) return; // List has one element

    if ((mid-l) >= THRESHOLD) mergesort(A, temp, l, mid);
    else inssort(A, l, mid-l+1);

    if ((r-mid) > THRESHOLD) mergesort(A, temp, mid+1, r);
    else inssort(A, mid+1, r-mid);

    // Do the merge operation. First, copy 2 halves to temp.
    for (i=l; i<=mid; i++) temp[i] = A[i];
    for (j=1; j<=r-mid; j++) temp[r-j+1] = A[j+mid];

    // Merge sublists back to array
    for (i=l,j=r,k=l; k<=r; k++)
        if (temp[i].compareTo(temp[j])<0) A[k] = temp[i++];
        else A[k] = temp[j--];
}

7.5 Quick Sort¶

The fastest known general-purpose in-memory sorting algorithm in practice.
It does not require the extra array needed by Merge Sort, so it is space efficient.
It is widely used in practice.
Steps:
1. Select a pivot element from the list (conceptually equivalent to BST root).
2. The array is divided into two partitions, [0, pivot-1] and [pivot+1, n-1].

static <E extends Comparable<? super E>> void qsort(E[] A, int i, int j) { // Quicksort
    int pivotindex = findpivot(A, i, j); // Pick a pivot
    DSutil.swap(A, pivotindex, j); // Stick pivot at end

   // k will be the first position in the right subarray
    int k = partition(A, i-1, j, A[j]);
    DSutil.swap(A, k, j); // Put pivot in place

   if ((k-i) > 1) qsort(A, i, k-1); // Sort left partition
    if ((j-k) > 1) qsort(A, k+1, j); // Sort right partition
}

static <E extends Comparable<? super E>> int findpivot(E[] A, int i, int j) {
    return (i+j)/2;
}

static <E extends Comparable<? super E>> int partition(E[] A, int l, int r, E pivot) {
    do { // Move bounds inward until they meet
        while (A[++l].compareTo(pivot)<0);
        while ((r!=0) && (A[--r].compareTo(pivot)>0));
        DSutil.swap(A, l, r); // Swap out-of-place values
    } while (l < r); // Stop when they cross
    DSutil.swap(A, l, r); // Reverse last, wasted swap
    return l; // Return first position in right partition
}

For a clearer code, see QuickSort.java.
Worst case: O(n^2), after the first pivot, the partitioning is always unbalanced as zero elements in the left partition and n-1 elements in the right partition (or vice versa).
Best case: O(n log n), when the pivot is always the median of the partition, so that the number of elements in the left and right partitions are equal.
Average case: O(n log n).
Selecting the pivot:
- Using random pivot is a good choice, but it is relatively expensive.
- A good choice is to use the median of three elements, the first, middle, and last elements.
- In our discussion, we chose the middle element as the pivot.
QuickSort is slow if n is small. For small n, Insertion Sort or Selection Sort is faster.

7.6 Heap Sort¶

It is based on the Heap data structure which uses the a Complete Binary Search Tree under the hood.
Heap tree is balanced, so it is space efficient and items can be inserted into the array at once, then heapify.
The time complexity of Heap Sort is O(n log n).
It is not faster than Quick Sort in practice, but it is the choice for sorting large sets that do not fit in memory.
Steps:
1. Build a heap from the initial array.
2. Repeatedly remove the largest element from the heap (dequeue) and insert it into the end of the result array (might be the same original array).
3. The dequeue operation includes heapify to maintain the heap property, then the largest element is guaranteed to be at the root.
4. Repeat until the heap is empty.

7.7 Bin Sort¶

Bin Sort or Bucket Sort depends on placing elements into a list of bins (buckets), each of which is a small array itself, then sorting each bin individually, then concatenating the bins (if needed).
Time complexity: O(n).
More: https://opendsa-server.cs.vt.edu/ODSA/Books/CS3/html/BinSort.html

7.7 Radix Sort¶

Radix sort is a modified version of bin sort, where values are assigned to bins based in their radix or base, that is, we start placing elements in bins based on their most significant digit (right most digit), then we keep repeating the process for the next digit until we reach the least significant digit (left most digit).
For keys of k digits, then all elements are reassigned to bins k times.
Time complexity: O(n) or O(n log n) for an input with distinct keys.

7.8 An Empirical Comparison of Sorting Algorithms¶

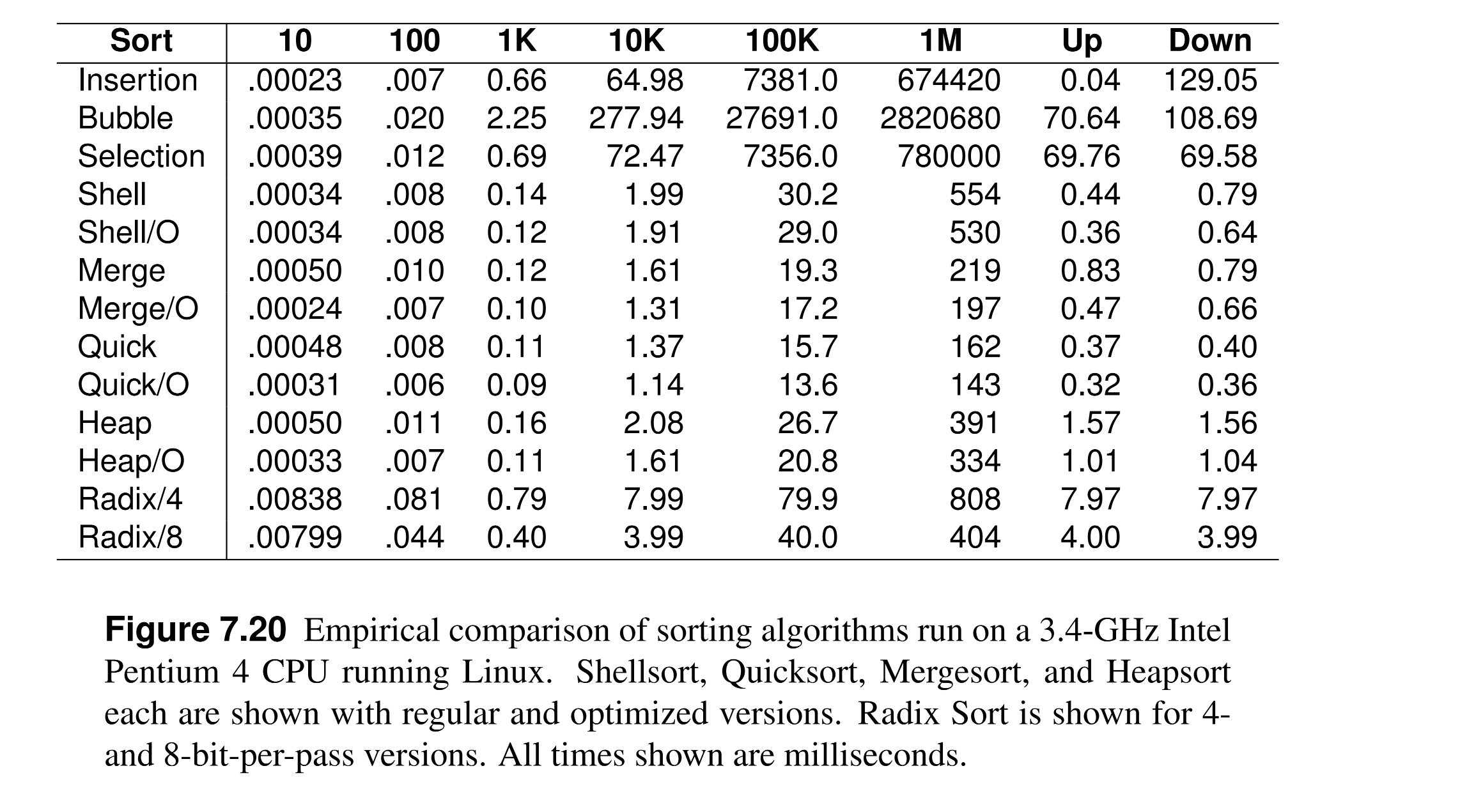
Quick Sort is the fastest in practice.
Asymptotic analysis for the sort problem:
- Omega(n) to Omega(n log n) lower bound, every algorithm must read every element at least once and detect if it is in the right place or not.

References¶

UoPeople (2023). CS 3303 Data Structures. Unit 5: Internal Sorting Techniques and Algorithms. Video Lecture https://my.uopeople.edu/mod/kalvidres/view.php?id=359076 ↩
Shaffer, C. (2011). A Practical Introduction to Data Structures and Algorithm Analysis. Blacksburg: Virginia. Tech. https://people.cs.vt.edu/shaffer/Book/JAVA3e20130328.pdf. Chapter 7: Internal Sorting. ↩

-	Insertion	Bubble	Selection
best case	Θ(n)	Θ(n2)	Θ(n2)
avg case	Θ(n2)	Θ(n2)	Θ(n2)
worst case	Θ(n2)	Θ(n2)	Θ(n2)

6. Internal Sorting Techniques and Algorithms¶

Introduction 1 2¶

7.2 Three Θ(n2) Sorting Algorithms¶

7.2.1 Insertion Sort¶

7.2.2 Bubble Sort¶

7.2.3 Selection Sort¶

7.2.4 The Cost of Exchange Sorting¶

7.3 Shell Sort¶

7.4 Merge Sort¶

7.5 Quick Sort¶

7.6 Heap Sort¶

7.7 Bin Sort¶

7.7 Radix Sort¶

7.8 An Empirical Comparison of Sorting Algorithms¶

References¶

Introduction ¹ ²¶