Skip to content

DA4. Kruskal’s Algorithm

Statement

In Chapter 11 of the Shaffer text, we are introduced to Kruskal’s Algorithm for determining a Minimum Spanning Tree within a graph. This algorithm is described as a greedy algorithm.

  • Describe in your own words how Kruskal’s algorithm works.
  • Articulate in your description what makes Kruskal’s algorithm ‘greedy’.

Include one or two examples to explain your thought process to show what is occurring and how the methodology works. Use APA citations and references for any sources used.

Answer

Introduction

A graph is a collection of vertices and edges that may be weighted. The weight of a graph is the sum of the weights of all its edges. A spanning tree of undirected connected graph G = (V,E) is a subgraph T that is a tree and contains every vertex of G.

Minimum Spanning Trees

A minimum spanning tree (MST) is a spanning tree of a graph with the smallest possible weight among all spanning trees. There may be multiple MSTs for a graph, if placing edges in a different order results in the same weight (Dekai, 2005).

MSTs have many applications, such as computing the shortest set of wires needed to connect a set devices, traveling salesman, and problems of similar nature. There are two common algorithms to find the MST of a graph: Prim’s algorithm and Kruskal’s algorithm. Both are greedy algorithms but they differ in the way they select the next edge to add to the MST (Shaffer, 2011).

Kruskal’s Algorithm

Kruskal’s algorithm is a greedy algorithm that grows a collection of trees (a forest) until the forest merges into a single tree. In other words, it starts by dividing the graph into a forest of |V| trees of single vertex each (V is the number of vertices in the graph). Then, it repeatedly selects the cheapest edge that does not create a cycle in the forest and adds it to the MST, slowly merging those trees into a single MST (Shaffer, 2011), and here is a step-by-step of how the algorithm works:

  • Create a forest of |V| trees, where each tree contains a single vertex.
  • Maintain a list of all edges that have not been added to the MST, sorted by weight in ascending order.
  • While the number of trees in the forest is greater than 1:
    • Select the edge with the smallest weight from the list.
    • If the edge connects two different trees, add it to the MST and merge the two trees into a single tree.
    • If the edge connects two vertices in the same tree, discard it to avoid creating a cycle.
  • Return the MST, which is the single tree left in the forest that contains all vertices.

Example

The following images show the steps of Kruskal’s algorithm to find the MST of a graph with four vertices A, B, C, and D, and four edges with weights 5, 2, 4, and 9. The algorithm starts by diving the graph into four trees, and starts with the node A.

Image 1: Step 1, splitting the graph into a forest
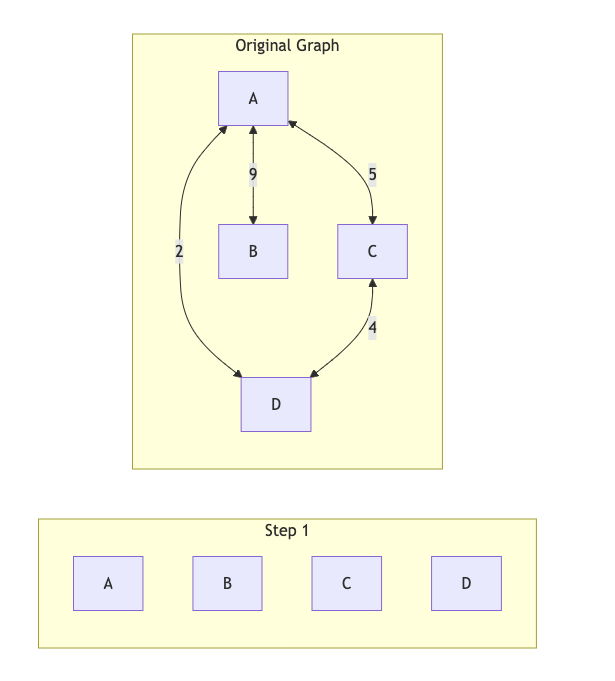Step 1

Next it adds the edge with weight 2 between A and D, merging both trees and reducing the number of trees to 3. In step 3, the vertex C is connected to D with an edge of weight 4, reducing the number of trees to 2.

Image 2: Step 2 + 3, adding edges to the MST
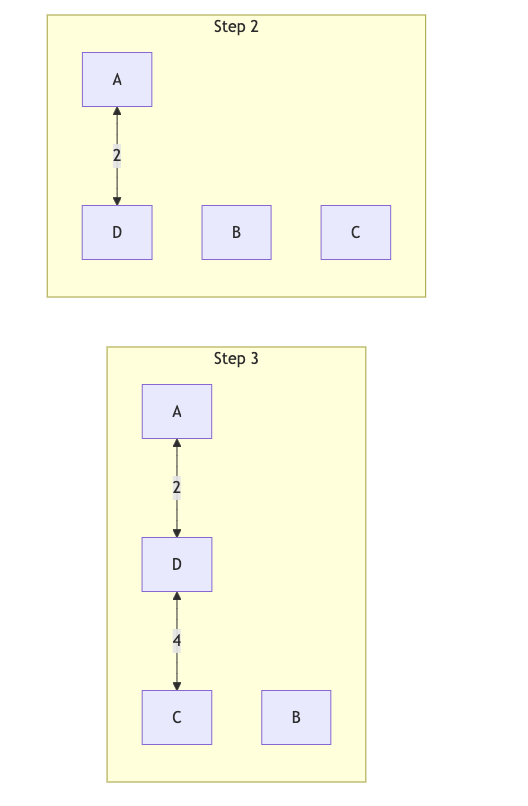Step 2

Finally, the edge between A and B with weight 9 is added, merging the last two trees into a single MST. The weight of the MST is 2 + 4 + 9 = 15. While the total weight of the graph is 5 + 2 + 4 + 9 = 20.

Image 3: Step 4, MST of the graph
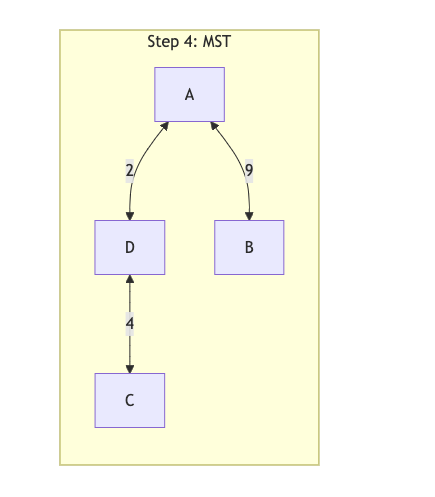Step 3

Conclusion

To conclude, Kruskal’s algorithm is a greedy algorithm because it makes the best (cheapest) choice at each step without worrying about the future or the overall picture. Collectively, the algorithm generates an MST which is the optimal solution for the problem of visiting all vertices with the smallest possible cost.

References