WA4. Monopoly¶
Statement¶
A monopoly firm faces a demand curve given by the following equation: P = $500 − 10Q, where Q equals quantity sold per day. Its marginal cost curve is MC = $100 per unit. Assume that the firm faces no fixed cost. You may wish to arrive at the answers mathematically, or by using a graph (the graph is not required to be presented), either way, please provide a brief description of how you arrived at your results.
a) How much will the firm produce?¶
The statement provides us with the demand curve and marginal cost (MC). According to the marginal decision rule, a profit-maximizing firm should increase output until the marginal benefit of an additional unit equals the marginal cost, that is marginal revenue (MR) equals marginal cost (MC).
The marginal revenue is the change in total revenue from selling one more unit of output. The marginal revenue can be extracted from the demand curve knowing that the slope of the marginal revenue curve is twice the slope of the demand curve (Rittenberg & Tregarthen, 2009, p. 261), which means that MR = 500 - 20Q.
We are assuming that firm is profit-maximizing, so we can set the marginal revenue equal to the marginal cost to find the quantity produced by the firm:
We can also see this on the graph (Free Econ Help, 2012):
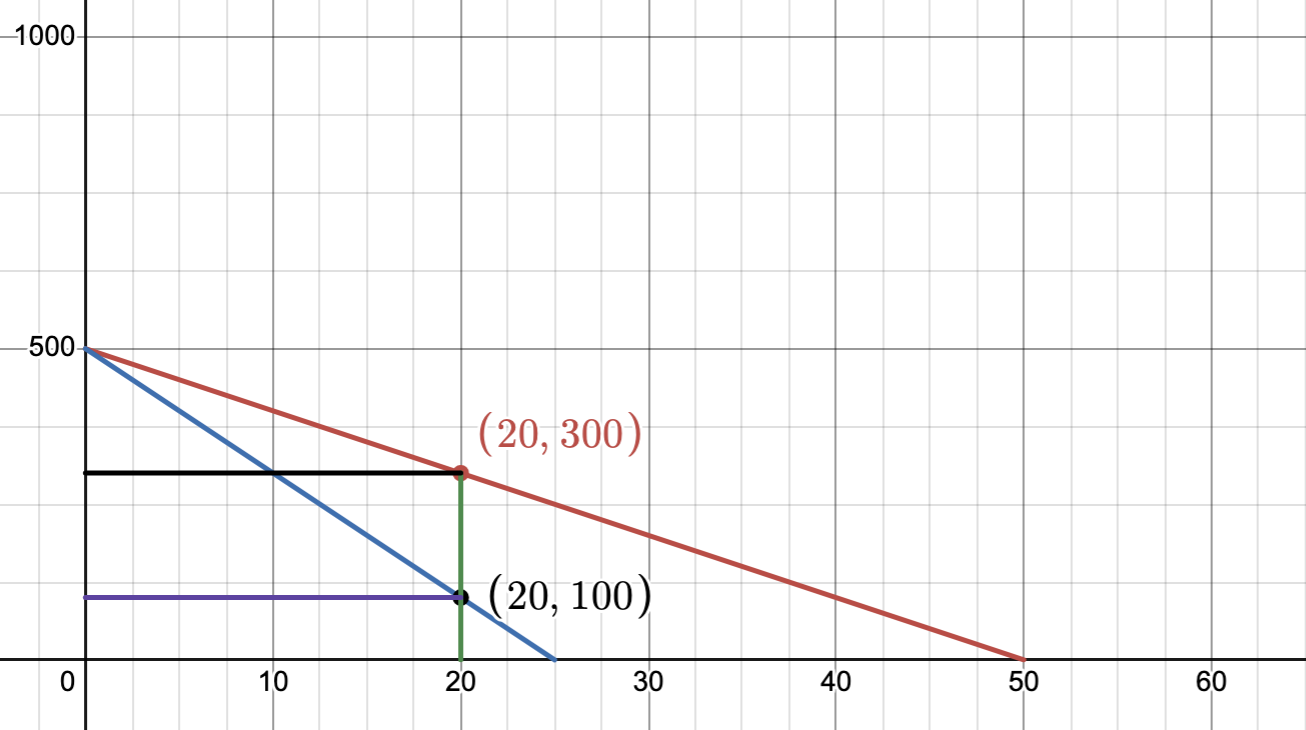
The red line represent the demand and the blue line represents the marginal cost. Notice the point (20, 100) which states that at 20 units of output, the marginal cost is equal to 100.
Thus, the firm will produce 20 units per day, or Q=20.
b) How much will it charge?¶
To find the price charged by the firm, we plug in the quantity produced into the demand curve:
We can also see this on the graph, if we took the (20,100) and intersected it with the demand curve, we would get the point (20,300).
Thus, the firm will charge $300 per unit.
c) Can you determine its profit per day? (Hint: you can; state how much it is.)¶
The profit per day can be calculated by subtracting the total cost from the total revenue. The total revenue is the price times the quantity sold, and the total cost is the marginal cost times the quantity sold. So:
From the graph, we can see that the total profit is the area of the rectangle formed by the points (20,300) and (20,100), and the vertical access which equals 20 * 200 = 4000. one more way from the graph is to calculate the marginal profit per item which is the difference between the price (20,300) and the marginal cost (20,100), and then multiply it by the quantity produced as 200 * 20 = 4000.
Thus, the firm will make a profit of $4000 per day.
d) Suppose a tax of $1,000 per day is imposed on the firm. How will this affect its price?¶
A tax on the company will be added to the fixed costs; it will not affect the marginal cost or the marginal revenue. It is called a lump-sum tax (Economics in Many Lessons, 2021). such tax does not vary with the quantity nor it increases the cost of producing the single unit.
Thus, the price will remain the same as $300.
e) How would the $1,000 per day tax its output per day?¶
As mentioned in the previous question, the tax will be added to the fixed costs, and it will not affect the output per day. The firm will continue to produce 20 units per day.
Thus, the firm will produce 20 units per day.
f) How would the $1,000 per day tax affect its profit per day?¶
The tax will be subtracted from the profit; we have computed the profit to be $4000, so the profit after the tax will be:
Thus, the firm will make a profit of $3000 per day after the tax.
g) Now suppose a tax of $100 per unit is imposed. How will this affect the firm’s price?¶
A tax of $100 per unit will increase the marginal cost by $100, thus the new marginal cost will be $200. To find the price we need to find the new quantity produced after setting MR = MC (Economics in Many Lessons, 2018):
So the firm will produce 15 units per day, and the price will be:
Thus, the firm will charge $350 per unit.
h) How would a $100 per unit tax affect the firm’s profit maximizing output per day?¶
As computed in the previous question, the firm will produce 15 units per day after the tax. Thus, the output per day will decrease from 20 units to 15 units while the price will increase from $300 to $350.
Notice the two points (15,200) and (15,350) on the new graph below:
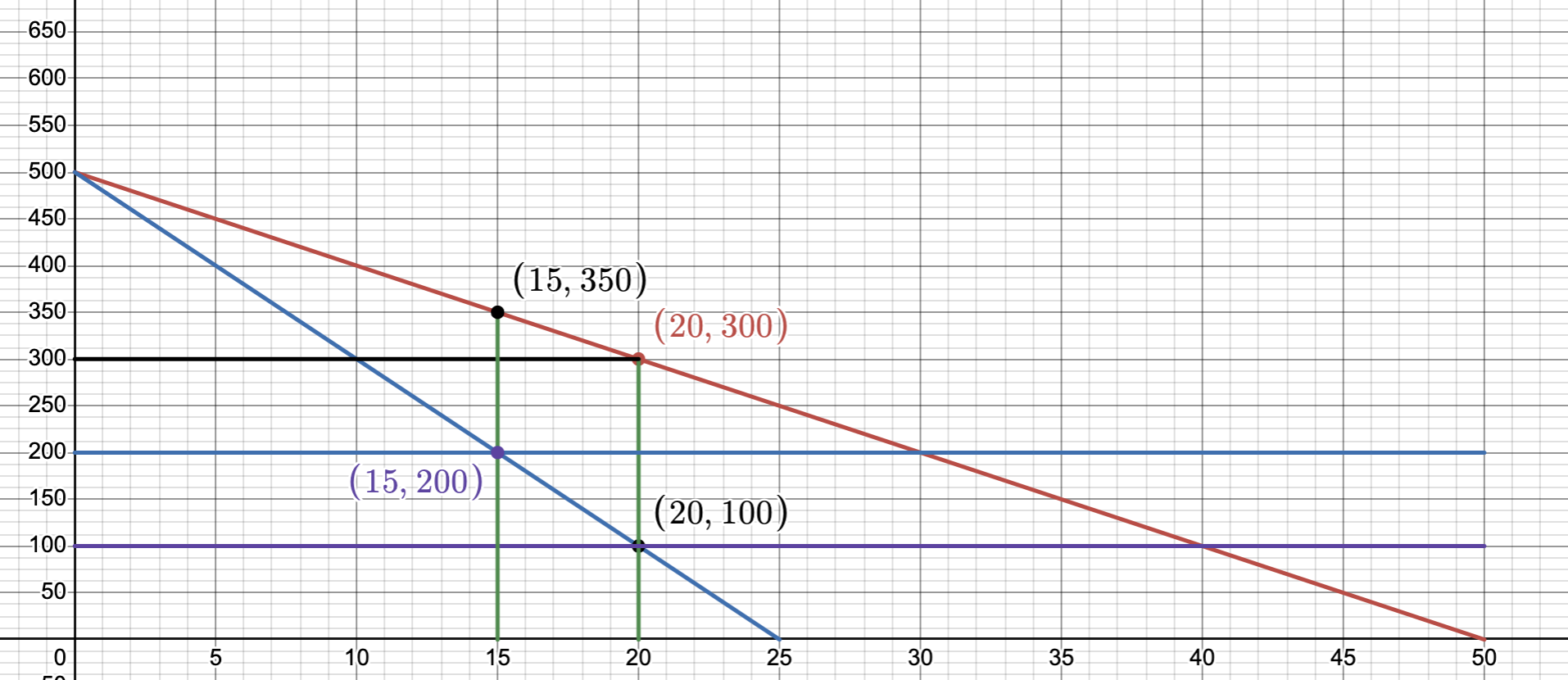
i) How would the $100 per unit tax affect the firms profit per day?¶
The tax will increase the marginal cost by $100, thus the new marginal cost will be $200. The firm will produce until the marginal revenue equals the new marginal cost:
Thus, the firm will make a profit of $2250 per day after the tax.
References¶
- CHAPTER 10 MARKET POWER: MONOPOLY AND MONOPSONY. (n.d.). https://uh.edu/~ghong/fina3334/sol_10.PDF
- Economics in Many Lessons. (2018). Analyzing a Tax on Monopoly Price and Output [YouTube Video]. In YouTube. https://www.youtube.com/watch?v=hRe8IwIinC0
- Economics in Many Lessons. (2021). Monopoly: Lump-Sum Tax [YouTube Video]. In YouTube. https://www.youtube.com/watch?v=0zazUL7qaLI
- Free Econ Help. (2012). How to find equilibrium price and quantity for a monopoly [YouTube Video]. In YouTube. https://www.youtube.com/watch?v=HArqf8NWo2Y&t=1s
- Rittenberg, L. & Tregarthen, T. (2009). Principles of Economics. Flat World Knowledge. https://my.uopeople.edu/pluginfile.php/1894547/mod_book/chapter/527796/Principles%20Of%20Economics%20Chapter10.pdf