Functions and Sequences¶
1 Functions¶
7.1 Definition and Notation¶
- Function: A function from a set A into a set B is a relation from A into B such that each element of A is related to exactly one element of the set B. The set A is called the domain of the function and the set B is called the codomain.
- The most important condition is: No element from the domain that have more than one image in the codomain, and all element of the domain must have images.
- Forms of function notations:
- A Function as a list of ordered pairs:
- Notation:
f = {(a, b), (c, d), (e, f), ...}wherea, c, e, ...are elements of the domain andb, d, f, ...are elements of the codomain. - Example:
f = {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)}wherefis a function that mapsA = {1, 2, 3, 4, 5}toB = {2, 4, 6, 8, 10}.
- Notation:
- A Function as a set of ordered pairs in set-builder notation:
- Notation:
f = {(x, y) | x ∈ A and y ∈ B}whereAis the domain andBis the codomain. - Example:
f = {(x, 3x) | x,y ∈ R}wherefis a function that mapsRtoRwhere each element inRis mapped to 3 times itself.
- Notation:
- The set of all possible functions from A to B:
- Notation:
B^AwhereB^A = {f | f is a function from A to B}. - Example:
B^A = {f1, f2}whereA = {1, 2, 3}andB = {a, b, c}andf1 = {(1, a), (2, b), (3, c)}andf2 = {(1, a), (2, c), (3, b)}.
- Notation:
- A Function as a formula( A definition based on images):
- Notation:
f(x) = expressionwherexis an element of the domain andexpressionis a formula that defines the function the equalsf = {(x, y) | x ∈ A and y ∈ B} - Example:
f(x) = x^2wherefis a function that mapsRtoRwhere each element inRis mapped to its square.
- Notation:
- A Function as a list of ordered pairs:
- Range of a function:
- The set of all images of the elements of the domain.
- Notation:
f(X) = {f(a) | a ∈ X} = {b ∈ Y | ∃a ∈ X such that f(a) = b}for functionf: X → Y. - The range of a function is a subset of its codomain.
- Examples of Non functions relations:
- Not all elements of the domain have images in the codomain:
- Example:
A={1, 2, 3}andB={a, b, c}andF={(1, a), (2, b)}. - F is not a function because
3(of A) does not have an image inB.
- Example:
- An element of the domain has more than one image in the codomain:
- Example:
A={1, 2, 3}andB={a, b, c}andF={(1, a), (1, b), (3, b)}. - F is not a function because
1(of A) has two images inBas(1, a)and(1, b). - The image of
1is not well defined.
- Example:
- Not all elements of the domain have images in the codomain:
- Examples of Non functions:

7.2 Properties of Functions¶
- Injective Function, Injection:
- A function f : A → B is injective if
∀a, b ∈ A, a ≠ b ⇒ f(a) ≠ f(b). - Also called one-to-one function.
- The condition for injective function is:
f(a) = f(b) ⇒ a = b. - That is, if two elements of the domain have the same image, then they must be the same element.
- Again, every element from the domain have exactly one image in the codomain, and no two elements of the domain have the same image.
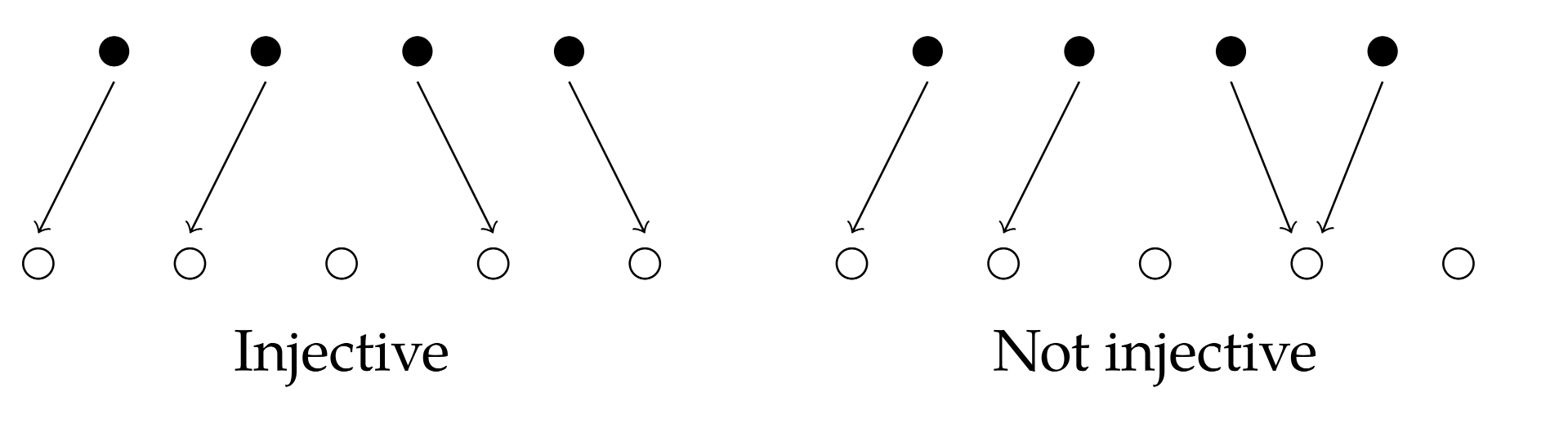
- A function f : A → B is injective if
-
Surjective Function, Surjection:
- A function f : A → B is surjective if
∀b ∈ B, ∃a ∈ A such that f(a) = b. - Also called onto function.
- That is, every element of the codomain is the image of at least one element of the domain.
- Again, No one element of the codomain is not used as an image.
- Again, every element from the codomain is connected to at least one element from the domain.
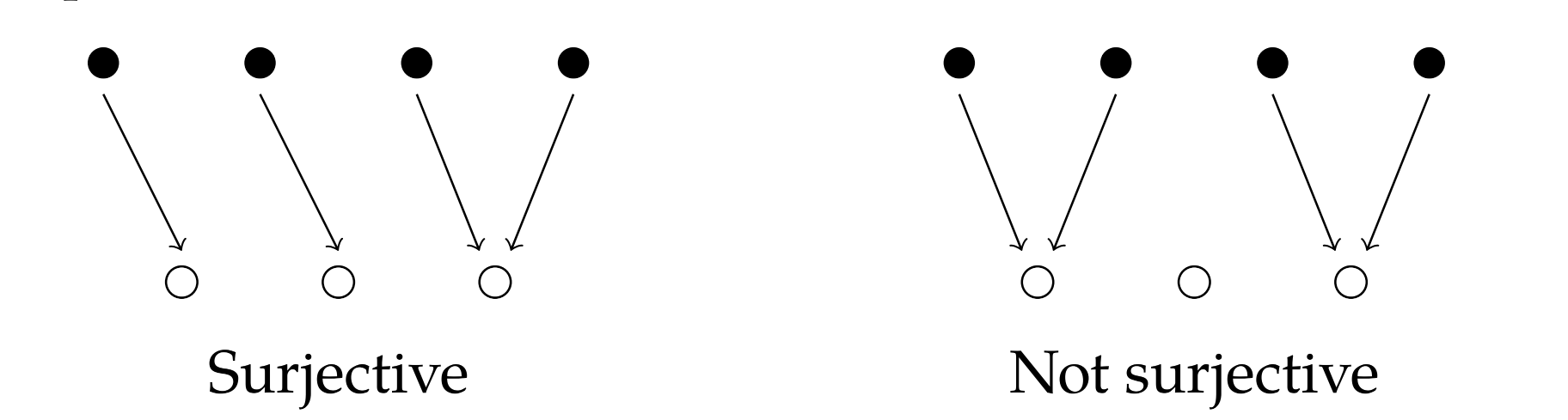
- A function f : A → B is surjective if
-
Bijective Function, Bijection:
- A function f : A → B is bijective if it is both injective and surjective.
- Also called one-to-one, onto functions.
- That is, every element of the codomain is the image of exactly one element of the domain, and every element of the codomain is used, and used for only one element of the domain.
- Cardinality. Two sets must have the same cardinality if the relationship between them is bijective.
- Countable Set: A set is countable if it is finite or if it has the same cardinality as some set of positive integers.
- Countably Infinite Set: A set is countably infinite if it has the same cardinality as the set of natural numbers
N. - Pigeonhole Principle:
- If you have more pigeons than pigeonholes, then at least one pigeonhole must contain more than one pigeon.
- If
nis a positive integer andn + 1objects are placed intonboxes, then at least one box contains two or more objects.
| Property | Meaning | English | English * (approximation, not very accurate) |
|---|---|---|---|
| Injective | \(∀a, b ∈ A, a ≠ b ⇒ f(a) ≠ f(b)\) | All elements in the domain have unique images in the codomain | All elements in the domain are used (unique images) |
| Surjective | \(∀b ∈ B, ∃a ∈ A, f(a) = b\) | All elements in the codomain have at least one image in the domain | All elements in the codomain are used |
- Example, let \(f,g: R -> R\) where \(f(x) = \sqrt[2]{x}\) and \(g(x) = \sqrt[3]{x}\)
| \(f(x) = \sqrt[2]{x}\) | \(g(x) = \sqrt[3]{x}\) | |
|---|---|---|
| Injective | No, Not all elements have unique images; e.g. negative numbers have no image. | Yes, all elements have unique cube root. |
| Surjective | Yes, negative numbers in codomain are used. e.g. \(f(16)= \pm2\) | Yes, all elements in codomain are used. |
| Bijective | No, not injective. | Yes, Injective and surjective |
7.3 Function Composition¶
- Function Equality:
- Two functions
fandgare equal if they have the same domain and the same codomain andf(x) = g(x)for allxin the domain.
- Two functions
- Function Composition:
- The composition of two functions
fandgis the functionf ◦ gdefined by(f ◦ g)(x) = f(g(x)). - Example:
f(x) = x^2andg(x) = x + 1then(f ◦ g)(x) = f(g(x)) = f(x + 1) = (x + 1)^2. - Also:
f ◦ g ≠ g ◦ fas in the previous example(g ◦ f)(x) = g(f(x)) = g(x^2) = x^2 + 1.
- The composition of two functions
- Function Composition Features is associative:
(f ◦ g) ◦ h = f ◦ (g ◦ h). - Powers of functions:
f^n = f ◦ f^(n-1)forn >= 1.f^1 = f.f^n+1 = f ◦ f^n.
- The composition of two injections is an injection:
f: A → Bandg: B → Care injections, theng ◦ f: A → Cis an injection. - The composition of two surjections is a surjection:
f: A → Bandg: B → Care surjections, theng ◦ f: A → Cis a surjection. - Identity Function:
- It is a function that maps each element of a set to itself.
- It is an onto function.
- Composing any function with the identity function does not change the function:
f ◦ I = I ◦ f = f.
7.3.3 Inverse Functions¶
- The inverse of a function
f: A → Bis a functiong: B → Asuch thatg ◦ f = Iandf ◦ g = I. - A function can only have one inverse or no inverse.
- The inverse function undoes the action of the original function.
- Example:
f: A → AwhereA={1,2,3}andf={(1,2), (2,3), (3,1)}.- The
f^-1 = {(2,1), (3,2), (1,3)}. where we swapped the first and second components of each pair inf.
- So an inverse function is a function that takes the image of an element, and returns back the original element.
- Example:
f(x) = x^2andg(x) = √xthenf ◦ g = Iandg ◦ f = I.f ◦ g = f(g(x)) = f(√x) = (√x)^2 = x.g ◦ f = g(f(x)) = g(x^2) = √(x^2) = x.
- Bijection functions are invertible.
2 Sequences¶
- A sequence is simply an ordered list of numbers. For example, here is a sequence:
0, 1, 2, 3, 4, 5, . . . .. - The order of the element in the sequence is important.
References¶
-
Doerr, A., & Levasseur, K. (2022). Applied discrete structures (3rd ed.). licensed under CC BY-NC-SA. https://discretemath.org/ads/chapter_7.html ↩
-
Levin, O. (2021). Discrete mathematics: An open introduction (3rd ed.). licensed under CC 4.0. Chapter 2: Sequences. ↩