DA4. Normalization vs Standardization¶
Statement¶
As part of your response explain and provide a detail example of how the min-max normalization and Z-score standardization values are computed and also explain why a data scientist might want to use either of these techniques.
Solution¶
- Both min-max normalization and Z-score standardization are used in data cleaning and transformation before model training.
- The goal of normalization is to make every datapoint have the same scale so each feature is equally important (Codecademy Team, 2018).
- In Min-Max normalization, each feature (independent variable, or predictor) is scaled to a value between 0 and 1 where each value is compared to the maximum and minimum values of the variable and the normalized value is used in place of the original value (Codecademy Team, 2018) according to the following formula:
x_normalized = (x - min(X)) / (max(X) - min(X))where ‘x’ is a value and ‘X’ represents the set of values for the variable. - Min-Max normalization still suffers from outliers (Codecademy Team, 2018).
- The Z-score normalization promises to avoid the problem of outliers (Codecademy Team, 2018) as it uses different formula for normalization:
x_normalized = (x - mean(X)) / standard_deviation(X)where ‘x’ is a value and ‘X’ represents the set of values for the variable. - Normalized data using Z-score normalization have negative values if the original value is less than the mean and positive values if the original value is greater than the mean (Codecademy Team, 2018) but the scale of the normalized data is less squashed and data points are more spread out on the axis.
- The z-score normalization deals better with the outliers due to the fact that standard deviation is less affected by individual values as the number of observations in the sample increases.
To test the behavior of the normalizations I used the following script:
x = c(10, 1000, 2000, 2344, 3550, 5000, 4333, 10000, 42000, 2333)
y =c(1, 11, 12, 14, 12, 45, 20, 23, 33, 19)
# Function to find global min and max for setting axis limits
globalMinMax <- function(a, b) {
c(min(c(min(a), min(b))), max(c(max(a), max(b))))
}
# Set up a 1x3 multi-panel plot
par(mfrow=c(1, 3))
# Global min and max for original data
limits_original = globalMinMax(x, y)
# Original plot
plot(x, y, main="Original", xlim=limits_original, ylim=limits_original)
# Min-Max Normalization
minMaxNormalization <- function(S) {
min_val <- min(S)
max_val <- max(S)
return((S - min_val) / (max_val - min_val))
}
x.minMaxNormalized = minMaxNormalization(x)
y.minMaxNormalized = minMaxNormalization(y)
limits_minMax = globalMinMax(x.minMaxNormalized, y.minMaxNormalized)
plot(x.minMaxNormalized, y.minMaxNormalized, main="Min-Max Normalized", xlim=limits_minMax, ylim=limits_minMax)
# Z-Score Normalization
zScoreNormalization <- function(S) {
mean_val <- mean(S)
sd_val <- sd(S)
return((S - mean_val) / sd_val)
}
x.zScoreNormalized = zScoreNormalization(x)
y.zScoreNormalized = zScoreNormalization(y)
limits_zScore = globalMinMax(x.zScoreNormalized, y.zScoreNormalized)
plot(x.zScoreNormalized, y.zScoreNormalized, main="Z-Score Normalized", xlim=limits_zScore, ylim=limits_zScore)
And the results are:
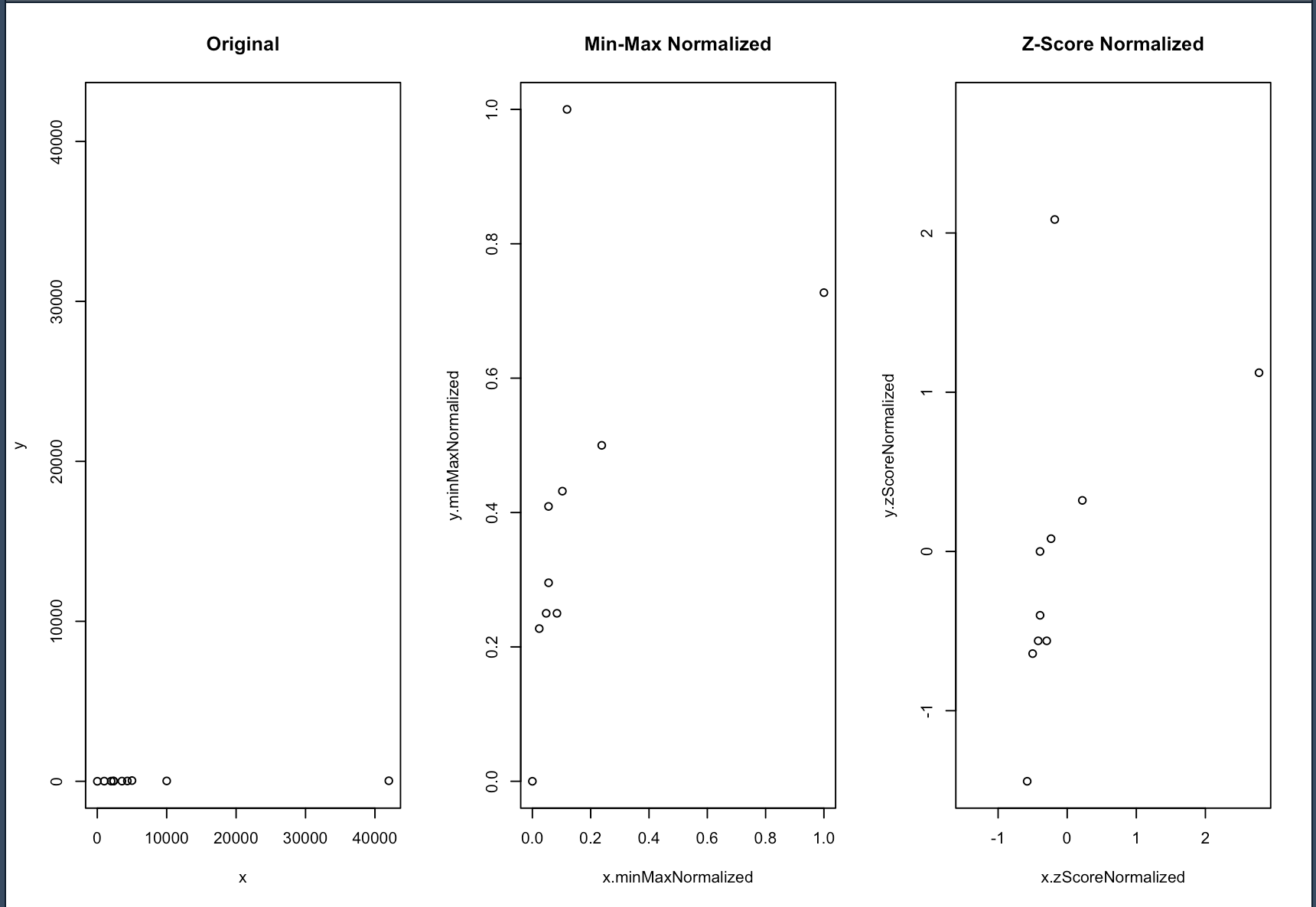
- Notice how the original data (to the left) is squashed and hardly visible in the plot.
- Min-Max normalization (in the middle) makes the data more visible but the scale is still squashed (due to the outliers).
- Z-Score normalization (to the right) makes the data more visible and the scale is less squashed.
References¶
- Codecademy Team. (2018). Normalization. https://www.codecademy.com/article/normalization
- Huddar M. (2022). Min-max normalization Z Score Normalization Data Mining Machine Learning Dr. Mahesh Huddar. YouTube. https://www.youtube.com/watch?v=-LC_PKBoZfk