DA8. Challenges of diagnostic plots¶
Statement¶
In your own words, identify a few common challenges faced while using diagnostic plots. Explain how these challenges can be addressed. Support your answers by providing relevant examples.
Answer¶
For any logistic or linear regression model, 4 conditions must be met or assumed:
- (1)- Residuals are nearly normal.
- (2)- Variability of residuals is nearly constant.
- (3)- Residuals are independent.
- (4)- Each variable is linearly related to the outcome.
Diagnostic plots are used to check these conditions; that is, before doing the regression analysis, we would use some diagnostic plots such as histogram of residuals, residuals against fitted values, residuals in order of their data collection, and residuals against each predictor variable to check if the assumptions are met.
A problem rises when the assumption (1) is not met, that is, the residuals are not normally distributed. This can be checked by looking at the histogram of residuals. Normal results would show a symmetric bell-shaped histogram (Image 1). However, if the histogram is skewed, normality is violated and it must be fixed by either using a different more suitable model or transforming the dependent variable. For example, if the residuals are skewed, we can use a log transformation to make them more symmetric (Diez, Barr, & Çetinkaya-Rundel, 2019).
| Image 1: Nearly normal histogram of residuals |
|---|
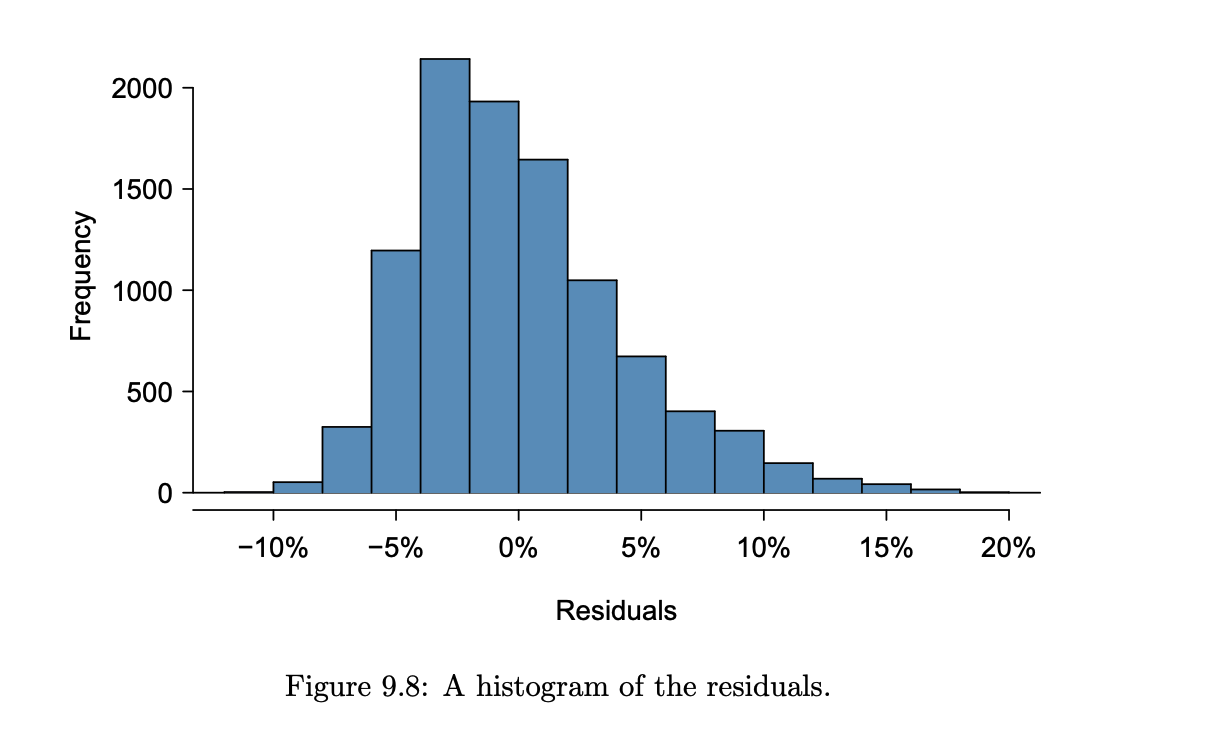 |
Another challenge is when the assumption (2) is not met, that is, the variability of residuals is not constant. This can be checked by plotting the absolute values of the residuals against the fitted values. If the residuals are spread out evenly across the fitted values, then the assumption is met. However, if there are clustering or specific patterns in the graph, then the assumption is violated. Image 2 shows a good example of residuals that are evenly spread out across the fitted values (Diez, Barr, & Çetinkaya-Rundel, 2019).
| Image 2: Residuals against fitted values |
|---|
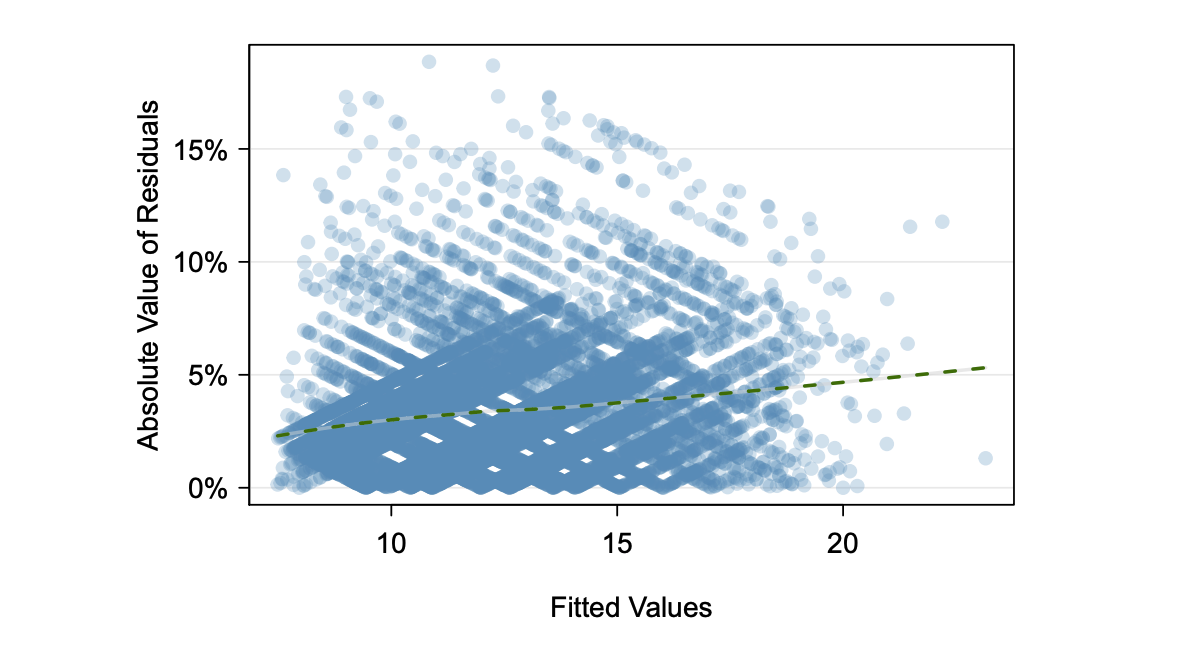 |
If the residuals are not independent (assumption 3), then the model is not valid. This can be checked by plotting the residuals in order of their data collection or time series. If there are patterns in the residuals then there was some bias in the data collection process; and the model is not valid.
Lastly, if the assumption (4) is not met, that is, each variable is not linearly related to the outcome, then the model is not valid. This can be checked by plotting the residuals against each predictor variable. If there is a pattern in the residuals, then the model is not valid. Image 3 shows a plot of residuals against 3 predictor variable, notice how the green line shows linearity (Diez, Barr, & Çetinkaya-Rundel, 2019).
| Image 3: Residuals against each predictor variable |
|---|
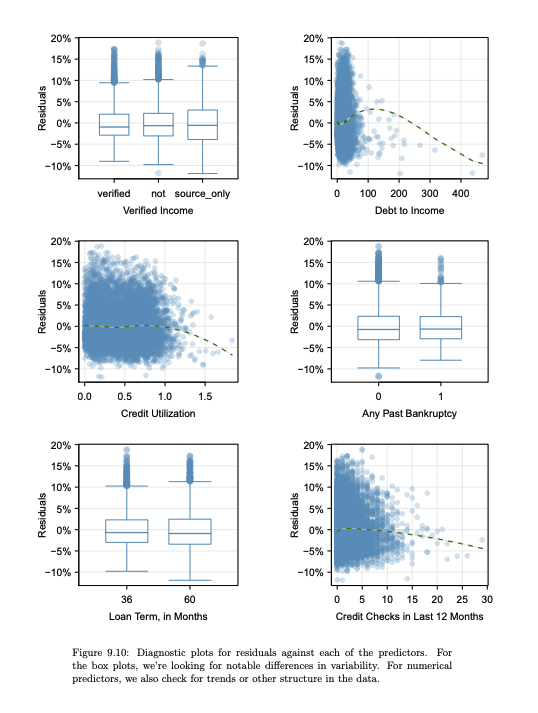 |
To conclude, outliers, clustering, and unexpected patterns are some of the challenges faced while using diagnostic plots relate to the data itself. The sensitivity of the diagnostic plots, how much data can it shows, and how easy it is to detect anomalies are another set of challenges that belong to the diagnostic plots themselves. In either way, careful examination of the problem, specifically noting any assumptions, or ignores made will increase the trustworthiness of the model and the results obtained from it.
References¶
- Diez, D. M., Barr, C. D., & Çetinkaya-Rundel, M. (2019). Openintro statistics - Fourth edition. Open Textbook Library. https://www.biostat.jhsph.edu/~iruczins/teaching/books/2019.openintro.statistics.pdf