algoritm toolbox¶
- the course link is here
week1: Programming Challenges¶
week2: Algorithmic Warm-up¶
week3: Greedy Algorithms¶
week4: Divide-and-Conquer¶
- braek the problem down into a set of non-overlaping sub-problems.
- sub-problems have the same type as the original
- we start solving sub problems in order.
- after solving all sub-problems we combine the results.
- since all sub-problems are of the same type, when we solve a sub-problem and iterate the solution
recurresivelyto the rest of the problems.
Definitions¶
- key, K: the elemet we are looking for.
- Array, A: the array we searching in
linear search¶
- loop through each elemnt of the array, determine if we find the element that we are looking for or not.
- after each search we face a
sub-array\(the main array execluded the previous element\) with the same type of problem. - we define the time that alogrithm takes as
recurrence relationwitch is an equationT. - worst case : element not found, defined by:
T(n) = T(n-1) + c=>cost = o(n). - best \(base\) case: empty array,
T(0) = c=>cost = o(1). - used in serch for the
free elemntsstored in alinked-list.
Binary search¶
- dividing problems into halves, also uses recurresion.
- starts by
sortingthe array. - we calculate the middle index
midof the sorted array, search for key at that index. - if
A[mid] == keywere done. else if:key > A[mid]we do another binary search on the top half of the sorted array. - else if
key < A[mid]we do binary search on the first half. - if the key is not found. we will return the best index to put our key in this
sorted-array. - worst case: element not found,
T(n) = T(n/2) + c=>cost = Log2 (n) - base case: empty array,
T(0) = c=>cost = o(1).
Augmented Array¶
- a sorted array that keep tracks element indexes in the original array before sorting.
polynomial multiplication¶
- usage:
- error-correcting code.
- large integer multiplication.
- generating functions.
- convolution in signal processing.
- input:
n=3, A=(3,2,5), B=(5,1,2)=> output:C=(15,13,33,9,10). - input:
n = 2, A = (3, 4) B = (1, 2)=> output:C=(3, 10, 8)corrseponding to:(3x+4) * (1x + 2) = 3x^2 + 10x + 8.
Naiive algorithm for solving polynomial multiplication problem¶
function MultPoly(A, B, n) {
/**
* A is polynomial as [3, 2, 5];
* B is another polynomial
* n is the hiegher degree of both polynomial (hieghest power of X)
*
*/
let product = new Array(2 * n - 1);
for (let i = 0; i < 2 * n - 1; i++) {
product[i] = 0;
}
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
product[i + j] = A[i] + B[j] + product[i + j];
}
}
return product;
}
- cost \(runtime\)
o(n^2);
Naiive divide-and-conquer algorithm for solving polynomial multiplication¶
function MultPoly2Wrapper(A, B, n){
// n needs to be divided by 2, if not add another degree to the polynomial,
// were its values is 0.
function MultPoly2(A, B, n, a1, b1){
/**
* A is polynomial as [3, 2, 5];
* B is another polynomial
* n is the hiegher degree of both polynomial (hieghest power of X)
* a1 specify the lower bound of the beginning of the sub-polynomials that are being multiplied
* b1 specify the lower bound of the beginning of the sub-polynomials that are being multiplied
* Mathematics Info in this photo: https://i.imgur.com/QZLIBQK.png
* programming info in this photo: https://i.imgur.com/UWKFjWB.png
*/
let R = new Array(2*n-1);
for(let i=0; i<2*n-1; i++){
R[i] = 0;
}
if(n == 1){
R[0] = A[a1] * B[b1];
return R;
}
//doing first half
for(let i=0; i<n-1; i++ ){
R[i] = MultPoly2 (A, B, n/2, a1, b1);
}
//we kept R[n-1] empty
//doing second half
for(let j=n; j<2*n-1; j++ ){
R[j] = MultPoly2 (A, B, n/2, a1 + n/2, b1 + n/2);
}
let D0E1= MultPoly2 (A, B, n/2, a1, b1 + n/2);
let D1E0= MultPoly2 (A, B, n/2, a1 + n/2, b1);
// ???????
let D1E1= MultPoly2 (A, B, n/2, a1 + n/2, b1 + n/2);
let D0E0= MultPoly2 (A, B, n/2, a1, b1);
//filling the empty elemnt R[n-1]
let R[n-1] = D1E0 + D0E1;
return R;
}
}
- cost
T(n) = 4 * T(n/2) + n*c=>4 * n * log(n) + n=> n2.
Faster divide-and-conquer algorithm for solving polynomial multiplication¶
/**
* Maths Explanation here: https://i.imgur.com/qa0to77.png
*/
function MultPoly3wrapper(A, B, n){
// n needs to be divided by 2, if not add another degree to the polynomial,
// were its values is 0.
let D1E1= //calcualted in the previous function;
let D0E0= //calculated before
let (D1+D0) + (E1+E0) = //calculated as the previous function.
}
karatsuba approach, do 3 multiplications instead of 4.- cost
T(n) = 3 * T(n/2) + n*c=>3 * n * log(n) + c * n=> nlog3 => n1.58.
Master Theorem¶
- for calculating cost in divide-and-concouer cost,
- binary search, problem divided into 2, each cost constant time
c:T(n) = T(n/2) +c=>log n - divide-and-conquer 1, problem divided into 4, each cost linear time
n:T(n) = 4 * T(n/2) + n * c=> nlog 4 => n2 - divide-and-conquer 2, problem divided into 3, each cost linear time
n:T(n) = 3 * T(n/2) + n * c=> nlog 3 => n1.58 - divide-and-conquer 3, problem divided into 2, each cost linear time
n:T(n) = 2 * T(n/2) + n * c=> nlog 2 => nlog\(n\) =>o(n log n) - more info [here]\([https://en.wikipedia.org/wiki/Master\_theorem\_\(analysis\_of\_algorithms\)](https://en.wikipedia.org/wiki/Master_theorem_%28analysis_of_algorithms%29))
then Theorom:
let T(n) = a * T(n/b) + o(n^d)
if d > logb ^a => T(n) = o(n^d)
if d = logb ^a => T(n) = o(n^d log n)
if d < logb ^a => T(n) = o(n^logb ^a)
selection sort¶
- find the minimum element => swap with first => reprat this process.
/**
* psudeo code here: https://i.imgur.com/IPq72GD.png
*/
function selectionSort(A) {
let n = A.length;
for (let i = 0; i < A.length; i++) {
let minIndex = i;
for (let j = i + 1; j < A.length; j++) {
if (A[j] < A[minIndex]) {
minIndex = j;
}
if (minIndex !== i) {
let c = A[minIndex];
swap(A, A[i], c);
// A[0,i] is now sorted.
}
}
}
return A;
}
function swap(A, B, C) {
let c = A.indexOf(C);
let b = A.indexOf(B);
let temp = B;
A[b] = C;
A[c] = temp;
}
- cost
o(n^2)
Merge sort¶
- split => sort splits => merge splits.
- merging has its own rules, evaluate the first elemnt from each arrays to be merged, we choose their minimum and put it in the result => repeat.
/**
* psudo code: https://i.imgur.com/rGmTGr4.png
*/
function mergeSort(A) {
if (A.length < 2) {
return A;
}
let m = Math.floor(A.length / 2);
let BB = mergeSort(A.slice(0, m));
let CC = mergeSort(A.slice(m, A.length));
let AA = merge(BB, CC);
return AA;
}
/**
* psuedo code: https://i.imgur.com/xlKWjXX.png
*/
function merge(B, C) {
let D = [];
while (B.length && C.length) {
if (B[0] <= C[0]) {
D.push(B[0]);
B.splice(0, 1);
} else {
D.push(C.shift());
}
}
while (B.length) {
D.push(B.shift());
}
while (C.length) {
D.push(C.shift());
}
return D;
}
- cost
n * log n
counting sort¶
- the
selection sortandmerge sortuseobject comparisionto complete the sort. - if the array is consesting from
repitive small intswe can applycounting sort - count occurences of each element => store counts to each elemnt \(n\) => fill up the result array by each elemnt reptitve with its corresponding count.
/**
* psuedo code: https://i.imgur.com/Nqb0cCg.png
* Now, works only for postivie ints.
*/
function countSort(A) {
let counts = {};
//let s = Math.min(...A);
let m = Math.max(...A);
// console.log('m', m);
for (let i = 0; i <= m; i++) {
counts[i] = 0;
}
//console.log(counts)
for (let i = 0; i < A.length; i++) {
// if(Object.keys(counts).includes(A[i].toString())){
// if(A.includes(Number(counts[i.toString()]))){
counts[A[i]]++;
// console.log('obj inside', counts);
//}
}
let countsArray = Object.keys(counts); //.every(e => e.toString());
// console.log('counts Array', countsArray);
// console.log('count obj', counts)
let result = [];
for (let i = 0; i < countsArray.length; i++) {
if (counts[i] > 0) {
let n = counts[i];
//console.log('n', n)
for (let j = 0; j < n; j++) {
result.push(Number(countsArray[i]));
}
}
}
return result;
}
- costs
o( Array.length + counts.length )=>o(n)
quick sort¶
- take first elemnt A[0] => rearrange the array so A[0] will be in the middle, all elements less or equal to A[0] will be on the left, all ements greater than A[0] will be on the right.
- A[0] is in its final positon => we need to sort
[left Array]and[right Array]=> repeat. partionorpivotwe choose it, either first or last element or in the middle or any element, however, it’s important to skip this element in thefor loop.
/**
* psuedo code: https://i.imgur.com/eczLG6T.png
*/
const quickSort = (array) => {
if (array.length < 2) return array;
const pivot = array[array.length - 1];
const left = [],
right = [];
for (let i = 0; i < array.length - 1; i++) {
if (array[i] < pivot) left.push(array[i]);
else right.push(array[i]);
}
return [...quickSort(left), pivot, ...quickSort(right)];
};
- best animation: https://www.youtube.com/watch?v=cnzIChso3cc
- costs
o(n^2)at worst: right or lift is empty,o(n log n)at average: right and left are nearly equal. - select our
pivotrandomly will give us more balanced left, right arrays => costs less, we should skipt it from the loop. - quick sort is not so fast on Arrays with
few uniqe elements: when you have few elemnets that are repeated. costso(n^2)
quick3¶
- quick sort on array with few unique elements.
- we partion to get 3 sub-arrays insted of 2: left, middle, right.
- left: All elements less than
pivot - middle: all elemnts equal to
pivot - lift: all elements greateer than
pivot
/**
* psuedo code: https://i.imgur.com/PaMqD6E.png
*/
const quickSort3 = (array) => {
if (array.length < 2) return array;
const pivot = array[array.length - 1];
const left = [],
right = [];
middle = [];
for (let i = 0; i < array.length - 1; i++) {
if (array[i] == pivot) middle.push(array[i]);
if (array[i] < pivot) left.push(array[i]);
else right.push(array[i]);
}
return [...quickSort3(left), ...middle, ...quickSort3(right)];
};
notes about quick sort¶
In-place algorithm: does not use extra auxilary space on the memory.elemeiate tail recursionorTail recursion call optimization: GeekForGeek article psuedo code- even if
random pivotis faster, it makes our program behaves differently on the same dataset, so it’s not welcomed. intro sort: when choosing the pivot, we select first, last and middle elemnts of the Array, then we compare thesepivots=> choose themedian pivotas owr pivot.
Intro quickSort¶
const IntroquickSort = (array) => {
if (array.length < 2) return array;
//comparing pivots
const pivot1 = array[0];
const pivot2 = array[Math.floor((array.length - 1) / 2)];
const pivot3 = array[array.length - 1];
//chosen pivot
let pivot = Math.min(pivot1, pivot2, pivot3);
let pivotIndex = array.indexOf(pivot);
const left = [],
right = [];
for (let i = 0; i < array.length; i++) {
if (i === pivotIndex) continue;
else if (array[i] < pivot) left.push(array[i]);
else right.push(array[i]);
}
return [...IntroquickSort(left), pivot, ...IntroquickSort(right)];
};
- costs
o(n log n)at worst.
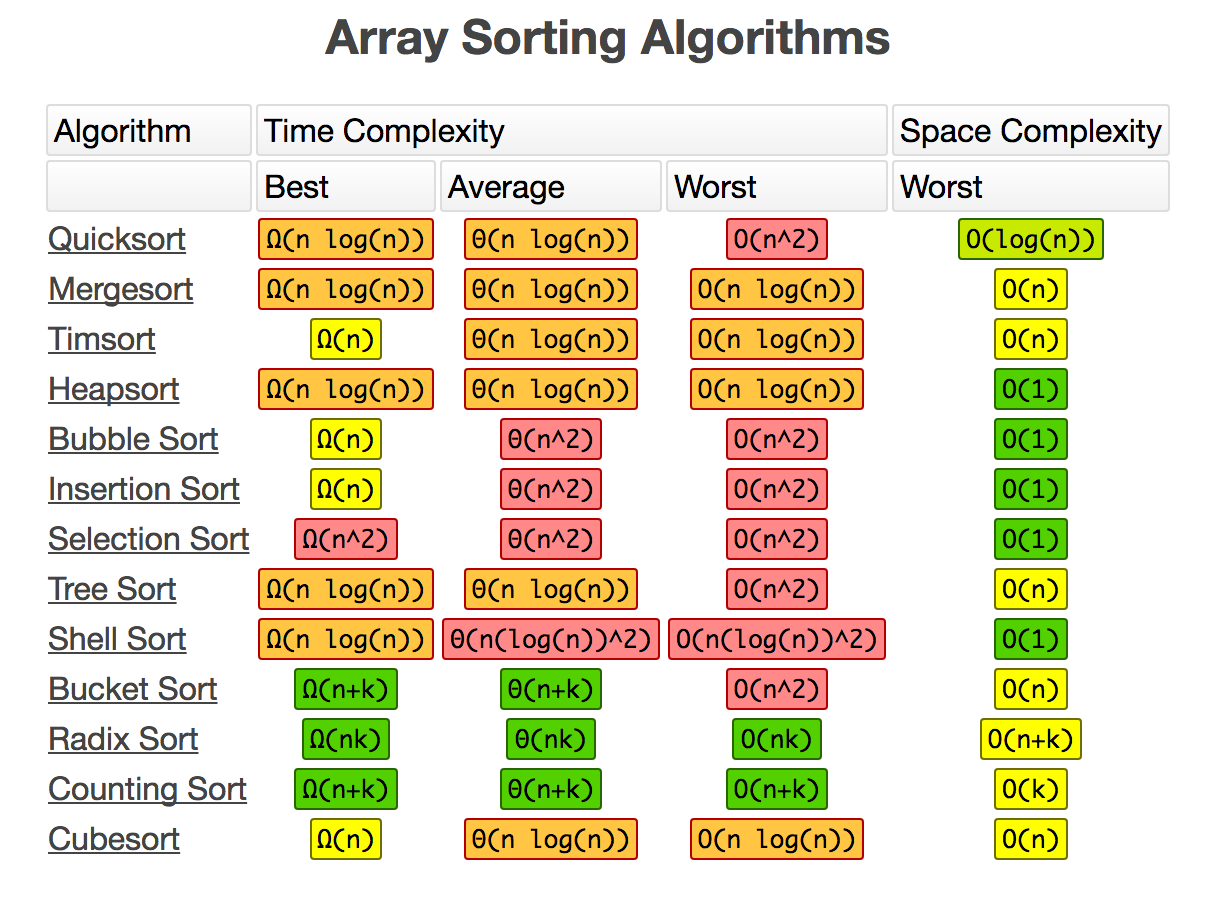
Array sorting algorithms cost summary¶
week5: Dynamic programming 1¶
Greedy change¶
psuedo code: https://i.imgur.com/3KGLxLJ.png
recursive change¶
psuedo code: https://i.imgur.com/DW0MLfG.png
dynamic prgramming change \(dp change\):¶
psuedo code: https://i.imgur.com/DL7Cpeo.png
Edit distance¶
psuedo code: https://i.imgur.com/iyCgqR1.png
resource¶
https://www.dropbox.com/s/qxzh146jd72188d/dynprog.pdf?dl=0
week 6: dynamic programming 2¶
knapsack with repetions¶
psudeo code: https://i.imgur.com/4hQNath.png
pdf: https://www.cc.gatech.edu/~rpeng/CS3510_F17/Notes/Oct2MoreDP.pdf
def unboundedKnapsack(W, n, val, wt):
# dp[i] is going to store maximum
# value with knapsack capacity i.
dp = [0 for i in range(W + 1)]
ans = 0
# Fill dp[] using above recursive formula
for i in range(W + 1):
for j in range(n):
if (wt[j] <= i):
dp[i] = max(dp[i], dp[i - wt[j]] + val[j])
return dp[W]
# Driver program
W = 100
val = [10, 30, 20]
wt = [5, 10, 15]
n = len(val)
print(unboundedKnapsack(W, n, val, wt))
knapsack with repetition¶
psuedo code: https://i.imgur.com/RDVqYi6.png
def knapSack(W , wt , val , n):
# Base Case
if n == 0 or W == 0 :
return 0
# If weight of the nth item is more than Knapsack of capacity
# W, then this item cannot be included in the optimal solution
if (wt[n-1] > W):
return knapSack(W , wt , val , n-1)
# return the maximum of two cases:
# (1) nth item included
# (2) not included
else:
return max(val[n-1] + knapSack(W-wt[n-1] , wt , val , n-1),
knapSack(W , wt , val , n-1))
# To test above function
val = [60, 100, 120]
wt = [10, 20, 30]
W = 50
n = len(val)
print knapSack(W , wt , val , n)
memoization¶
psuedo code: https://i.imgur.com/k2tkdnd.png
iterative algorithm: starts from the smaller problem into the larger onesrecursive algirithm: starts from the largest problem into the smaller ones.- resursive is slower.
placing parentheses¶
- you take an arithmetic operation and choose where to put parentheses so it will maximize its output